Đề bài
Cho \(h.bs.23,\) trong đó \(OA = 3,\) \(O'A = 2,\) \(AB = 5.\) Độ dài \(AC\) bằng:
\((A)\) \(\displaystyle{{10} \over 3}\) ; \((B)\) \(3,5\) ;
\((C)\) \(3\) ; \((D)\) \(4.\)
Hãy chọn phương án đúng.
Phương pháp giải - Xem chi tiết
Quy về xét hai tam giác đồng dạng theo trường hợp góc - góc
Lời giải chi tiết
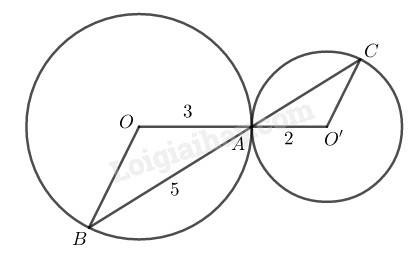
Ta có: \(\Delta OAB\) cân tại O (do \(OA=OB)\) nên \(\widehat {OBA}=\widehat {OAB}\)
\(\Delta O'AC\) cân tại O' (do \(O'A=O'C)\) nên \(\widehat {O'CA}=\widehat {O'AC}\)
Mà \(\widehat {OAB}=\widehat {O'AC}\) (đối đỉnh)
\(\Rightarrow \widehat {OBA}=\widehat {OAB}=\widehat {O'AB}=\widehat {O'AC}\)
Nên \(\Delta OAB ∽ \Delta O'AC\;\;(g.g)\)
\(\Rightarrow \dfrac{OA}{O'A}=\dfrac{AB}{AC}\)
\(\Rightarrow AC=\dfrac{AB.O'A}{OA}=\dfrac{5.2}{3}=\dfrac{10}{3}\)
Vậy chọn \((A).\)
dapandethi.vn
