Bài 5 trang 103 SBT toán 9 tập 1
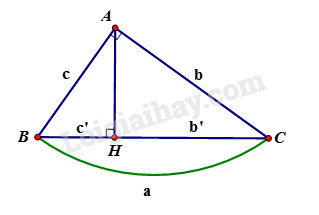
Giải bài 5 trang 103 sách bài tập toán 9. Cho tam giác ABC vuông tại A, đường cao AH (h.5). Giải bài toán trong mỗi trường hợp sau: AH = 16, BH = 25....
Bài 6 trang 103 SBT toán 9 tập 1
Giải bài 6 trang 103 sách bài tập toán 9. Cho tam giác vuông với các cạnh góc vuông có độ dài là 5 và 7, kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và các đoạn thẳng và nó chia ra trên cạnh huyền.
Bài 8 trang 103 SBT toán 9 tập 1
Giải bài 8 trang 103 sách bài tập toán 9. Cạnh huyền của một tam giác vuông lớn hơn một cạnh góc vuông là 1cm và tổng của hai cạnh góc vuông lớn hơn cạnh huyền 4cm. Hãy tính các cạnh của tam giác vuông này.
Bài 9 trang 104 SBT toán 9 tập 1
Giải bài 9 trang 104 sách bài tập toán 9. Một tam giác vuông có cạnh huyền là 5 và đường cao ứng với cạnh huyền là 2. Hãy tính cạnh nhỏ nhất của tam giác vuông này.
Bài 10 trang 104 SBT toán 9 tập 1
Giải bài 10 trang 104 sách bài tập toán 9. Cho một tam giác vuông. Biết tỷ số hai cạnh góc vuông là 3 : 4 và cạnh huyền là 125cm. Tính độ dài các cạnh góc vuông và hình chiếu của các cạnh góc vuông trên cạnh huyền.
Bài 12 trang 104 SBT toán 9 tập 1
Giải bài 12 trang 104 sách bài tập toán 9. Hai vệ tinh đang bay ở vị trí A và B cùng cách mặt đất 230km có nhìn thấy nhau hay không nếu khoảng cách giữa chúng theo đường thẳng là 2200km?
Bài 15 trang 104 SBT toán 9 tập 1
Giải bài 15 trang 104 sách bài tập toán 9. Giữa hai tòa nhà (kho và phân xưởng) của một nhà máy, người ta xây dựng một băng chuyền AB để chuyển vật liệu...
Bài 16 trang 104 SBT toán 9 tập 1
Giải bài 16 trang 104 sách bài tập toán 9. Cho tam giác có độ dài các cạnh là 5, 12, 13. Tìm góc đối diện với cạnh có độ dài 13 của tam giác.
Bài 18 trang 105 SBT toán 9 tập 1
Bài 18 trang 105 sách bài tập toán 9. Cho tam giác ABC vuông tại A, vẽ đường cao AH. Chu vi của tam giác ABH là 30cm và chu vi của tam giác ACH là 40cm. Tính chu vi của tam giác ABC.
Bài 19 trang 105 SBT toán 9 tập 1
Giải bài 19 trang 105 sách bài tập toán 9. Cho tam giác ABC vuông tại A có cạnh AB = 6cm và AC = 8cm. Các đường phân giác trong và ngoài của góc B cắt đường thẳng AC lần lượt tại M và N. Tính các đoạn thẳng AM và AN.
Bài 20 trang 105 SBT toán 9 tập 1
Giải bài 20 trang 105 sách bài tập toán 9. Cho tam giác vuông ABC. Từ một điểm M bất kì trong tam giác kể MD, ME, MF lần lượt vuông góc với các cạnh BC, AC, AB
Bài 1.6 phần bài tập bổ sung trang 106 SBT toán 9 tập 1
Giải bài 1.6 phần bài tập bổ sung trang 106 sách bài tập toán 9. Đường cao của một tam giác vuông kể từ đỉnh góc vuông chia cạnh huyền thành hai đoạn, trong đó đoạn lớn bằng 9cm. Hãy tính cạnh huyền của tam giác vuông đó nếu hai cạnh góc vuông có tỉ lệ 6 : 5.
Bài 1.9 phần bài tập bổ sung trang 106 SBT toán 9 tập 1
Giải bài 1.9 phần bài tập bổ sung trang 106 sách bài tập toán 9. Cho tam giác ABC vuông cân tại A, đường trung tuyến BM. Gọi D là chân đường vuông góc kẻ từ C đến BM và H là chân đường vuông góc kẻ từ D đến AC. Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ? Tại sao ?
Bài 1.10 phần bài tập bổ sung trang 106 SBT toán 9 tập 1
Giải bài Bài 1.10 phần bài tập bổ sung trang 106 sách bài tập toán 9. Cho hình thang ABCD vuông tại A có cạnh đáy AB bằng 6cm, cạnh bên AD bằng 4cm và hai đường chéo vuông góc với nhau. Tính độ dài các cạnh DC, CB và đường chéo DB.