Đề bài
Dựng một cung chứa góc \(60^\circ\) trên đoạn thẳng \(AB\) cho trước.
Phương pháp giải - Xem chi tiết
Cách vẽ cung chứa góc \(\alpha :\)
+) Vẽ đường trung trực \(d\) của đoạn thẳng \(AB.\)
+) Vẽ tia \(Ax\) tạo với \(AB\) góc \(\alpha.\)
+) Vẽ đường thẳng \(Ay\) vuông góc với \(Ax\). Gọi \(O\) là giao điểm của \(Ay\) với \(d.\)
+) Vẽ cung \(\overparen{AmB},\) tâm \(O,\) bán kính \(OA\) sao cho cung này nằm ở nửa mặt phẳng bờ \(AB\) không chứa tia \(Ax.\)
+) \(\overparen{AmB}\) được vẽ như trên là một cung chứa góc \(\alpha.\)
Lời giải chi tiết
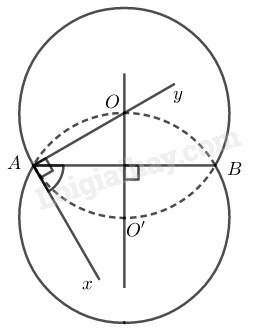
Cách dựng:
− Dựng đoạn thẳng \(AB.\)
− Dựng tia \(Ax\) sao cho \(\widehat {BAx} = 60^\circ \).
− Dựng đường thẳng \(d\) là trung trực của \(AB.\)
− Dựng tia \(Ay ⊥ Ax\) tại \(A.\)
− Tia \(Ay\) cắt đường thẳng \(d\) tại \(O.\)
− Dựng cung tròn tâm \(O\) bán kính \(OA.\)
− Dựng \(O'\) đối xứng với \(O\) qua \(AB.\)
− Dựng cung tròn tâm \(O’\) bán kính \(O’A.\)
Ta có cung chứa góc \(60^\circ \) vẽ trên đoạn \(AB\) cho trước.
dapandethi.vn
