Đề bài
Tìm dư R trong phép chia đa thức A cho đa thức B rồi viết dưới dạng \(A = B.Q + R\)
a) \(A = 3{x^4} + {x^3} + 6x - 5\) , \(B = {x^2} + 1\) ;
b) \(A = 10{x^3} + 27{x^2} + 14x + 5\) ; \(B = {x^2} + 2x\).
Lời giải chi tiết
a)
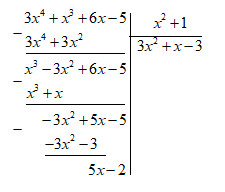
Dư R trong phép chia A cho B là \(R = 5x - 2\)
\(A = B.Q + R \Rightarrow \left( {3{x^4} + {x^3} + 6x - 5} \right) = \left( {{x^2} + 1} \right)\left( {3{x^2} + x - 3} \right) + 5x - 2\)
b)
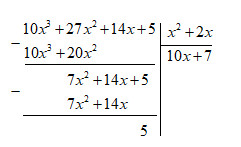
Dư R trong phép chia A cho B là \(R = 5\) và \(A = B.Q + R\)
\(10{x^3} + 27{x^2} + 14x + 5 = \left( {{x^2} + 2x} \right)\left( {10x + 7} \right) + 5\)
dapandethi.vn
