Đề bài
Cho đường tròn \((I)\) nội tiếp tam giác \(ABC.\) Các tiếp điểm trên \(AC, AB\) theo thứ tự là \(D, E.\) Cho \(BC = a,\) \(AC = b,\) \(AB = c.\) Tính độ dài các đoạn tiếp tuyến \(AD, AE\) theo \(a, b, c.\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì điểm đó cách đều hai tiếp điểm.
Lời giải chi tiết
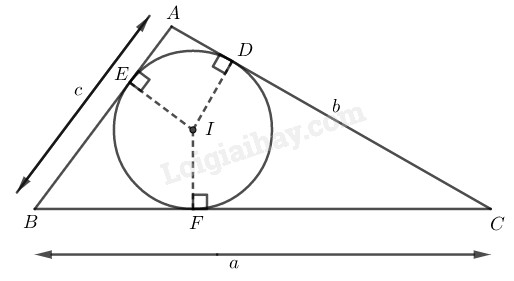
Gọi \(F\) là tiếp điểm của đường tròn \((I)\) với \(BC.\)
Theo tính chất của hai tiếp tuyến cắt nhau, ta có:
\(AE = AD\)
\( BE = BF\)
\( CD = CF\)
Mà: \(AE = AB – BE\)
\( AD = AC – CD\)
Nên: \(AE + AD = (AB –BE) + (AC – CD)\)
\( = AB + AC – (BE + CD)\)
\( = AB + AC – (BF + CF) \)
\( = AB + AC – BC\)
Suy ra: \(AE + AD = c + b – a\)
Hay: \(AE = AD =\displaystyle {{c + b - a} \over 2}\)
dapandethi.vn
