Đề bài
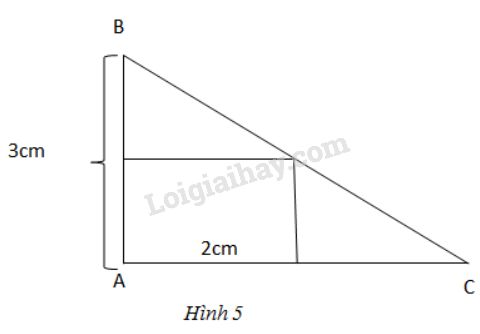
Đố: Lan có một miếng bìa hình tam giác ABC vuông tại A, cạnh AB = 3cm. Lan tính rằng nếu cắt từ miếng bìa đó ra một hình chữ nhật ấy có diện tích bằng một nửa diện tích của miếng bìa ban đầu. Tính độ dài cạnh AC của tam giác ABC.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Bước 1: Đặt độ dài cạnh AC là ẩn, đặt điều kiện cho ẩn
Bước 2: Biểu diễn các đại lượng còn lại theo ẩn.
Bước 3: Lập phương trình biểu diễn mối quan hệ giữa các đại lượng và giải phương trình đó.
Bước 4: Kết luận.
Lời giải chi tiết
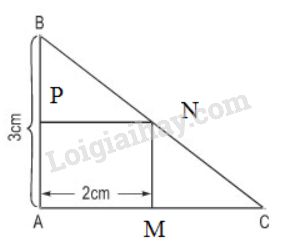
Gọi \(x (cm)\) là độ dài cạnh \(AC (x >2 )\).
Gọi hình chữ nhật là \(MNPA\) (như hình vẽ) thì \(MC = x – 2 (cm)\)
Vì \(MN // AB\) nên \(\dfrac{{MN}}{{AB}} = \dfrac{{MC}}{{AC}}\) (hệ quả của định lí TaLet)
\( \Rightarrow MN = \dfrac{{AB.MC}}{{AC}} = \dfrac{{3\left( {x - 2} \right)}}{x}(cm)\)
Diện tích hình chữ nhật \(MNPA\) là: \(2.\dfrac{{3\left( {x - 2} \right)}}{x} = \dfrac{{6\left( {x - 2} \right)}}{x}\)
Diện tích hình tam giác \(ABC\) là: \(\dfrac{1}{2}AB.AC = \dfrac{1}{2}.3.x = \dfrac{3}{2}x\)
Vì diện tích hình chữ nhật \(MNPA\) bằng một nửa diện tích hình tam giác \(ABC\) nên ta có phương trình:
\(\eqalign{
& {3 \over 2}x = 2.{{6\left( {x - 2} \right)} \over x} \cr
& \Leftrightarrow {{3x.x} \over {2x}} = {{2.2.6\left( {x - 2} \right)} \over {2x}} \cr
& \Rightarrow 3{x^2} = 24x - 48 \cr
& \Leftrightarrow 3{x^2} - 24x + 48 = 0 \cr
& \Leftrightarrow {x^2} - 8x + 16 = 0 \cr
& \Leftrightarrow {x^2} - 2.x.4 + {4^2} = 0 \cr
& \Leftrightarrow {\left( {x - 4} \right)^2} = 0 \cr
& \Leftrightarrow x - 4 = 0 \cr
& \Leftrightarrow x = 4\text{ (thỏa mãn)} \cr} \)
Vậy \(AC = 4cm\).
dapandethi.vn
