Đề bài
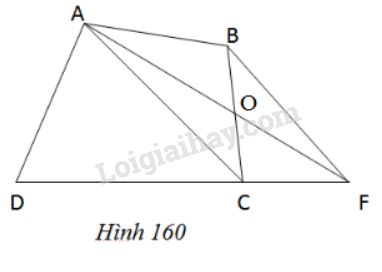
Trên hình \(160\) \((AC//BF)\), hãy tìm tam giác có diện tích bằng diện tích của tứ giác \(ABCD\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng cách tính diện tích tam giác, tứ giác.
Lời giải chi tiết
Gọi \(O\) là giao điểm của \(AF\) và \(BC\).
Ta có \(\Delta A{\rm{D}}F\) có diện tích bằng diện tích tứ giác \(ABCD\).
Thật vậy, do \( AC// BF\) nên \({S_{ABC}} = {S_{AFC}}\) vì có cùng đáy \(AC\) và cùng chiều cao là khoảng cách giữa hai đường thẳng song song \(AC, BF.\)
Ta có: \({S_{ABC}} = {S_{AFC}}\) (chứng minh trên)
\( \Rightarrow {S_{ABO}} + {S_{ACO}} = {S_{CF{\rm{O}}}} + {S_{AC{\rm{O}}}}\)
\(\Rightarrow {S_{ABO}} = {S_{CFO}}\).
Do đó \({S_{ADF}} = {S_{AOCD}} + {S_{CFO}} \)\(= {S_{AOCD}} + {S_{ABO}}= {S_{ABCD}}\)
Vậy \({S_{ADF}} = {S_{ABCD}}\)
dapandethi.vn
