Đề bài
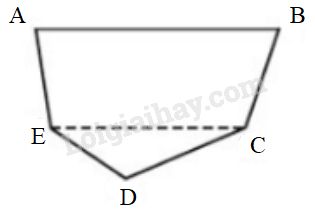
Thực hiện các phép vẽ và đo cần thiết để tính diện tích một đám đất có dạng như hình \(154\), trong đó \(AB // CE\) và được vẽ tỉ lệ \(\dfrac{1}{5000}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Diện tích hình thang bằng một nửa tích của tổng hai đáy với chiều cao.
$$S = {1 \over 2}\left( {a + b} \right).h$$
- Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
$$S = {1 \over 2}ah$$
Lời giải chi tiết
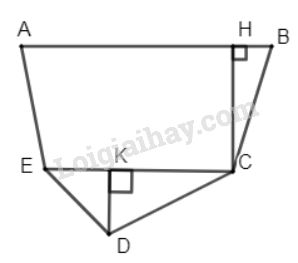
Chia đám đất \(ABCDE\) thành hình thang \(ABCE\) và tam giác \(ECD.\) Cần vẽ đường cao \(CH\) của hình thang và đường cao \(DK\) của tam giác. Thực hiện các phép đo chính xác đến \(mm\) ta được \(AB = 30\,mm, CE = 26\,mm,\) \(CH = 13\,mm, DK = 7\,mm.\)
Vì bản đồ được vẽ với tỉ lệ xích \(\dfrac{1}{5000}\) nên trên thực tế:
AB = 30. 5 000 = 150 000 mm = 150 m
CE = 26 . 5 000 = 130 000 mm = 130 m
CH = 13 . 5 000 = 65 000 mm = 65 m
DK = 7 . 5 000 = 35 000 mm = 35 m
\({S_{ABCE}}=\dfrac{\left ( AB+EC \right ).CH}{2} \)\(\,= \dfrac{\left ( 150 + 130 \right ). 65}{2} =9100\) \(({m^2})\)
\({S_{ECD}}=\dfrac{1}{2} EC. DK = \dfrac{1}{2} .130.35= 2275\) \(({m^2})\)
Do đó \({S_{ABCDE}} = {S_{ABCE}} + {S_{ECD}} = 9100 + 2275 \)\(\,= 11375\) \(({m^2})\)
