Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, \(\widehat B\) = 600. Biết rằng có một hình nón nội tiếp hình chóp đã cho với bán kính đáy là r, góc giữa đường sinh và đáy hình nón là \(\beta .\)
LG 1
Tính diện tích xung quanh và thể tích hình nón.
Lời giải chi tiết:
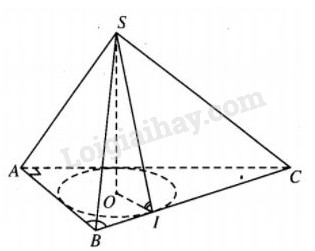
Đáy hình nón trong bài toán là đường tròn nội tiếp tam giác ABC.
Đường cao hình nón là SO (S là đỉnh của hình chóp ).
Gọi I là điểm tiếp xúc của BC với đường tròn nội tiếp \(\Delta ABC\) thì \(OI \bot BC\) và \(SI \bot BC\) nên \(\widehat {SIO}\) =\(\beta .\)
Khi đó, chiều cao hình nón là
\(h = SO = OI\tan \beta = r\tan \beta ,\)
Độ dài đường sinh hình nón là
\(l = SI = {{OI} \over {\cos \beta }} = {r \over {\cos \beta }}.\)
Vậy diện tích xung quanh của hình nón là
\({S_1} = \pi rl = \pi r.{r \over {\cos \beta }} = {{\pi {r^2}} \over {\cos \beta }}.\)
Thể tích hình nón là
\({V_1} = {1 \over 3}\pi {r^2}h = {1 \over 3}\pi {r^2}.r.\tan \beta = {1 \over 3}\pi {r^3}\tan \beta .\)
LG 2
Tính diện tích xung quanh và thể tích hình chóp.
Lời giải chi tiết:
Dễ thấy ba đường cao của ba mặt bên hình chóp S.ABC bằng nhau và cùng bằng SI.
Diện tích xung quanh của hình chóp là
\({S_2} = {1 \over 2}\left( {AB + AC + BC} \right).SI\)
Mặt khác \(AC = AB\sqrt 3 ,BC = 2AB,\)
\(\eqalign{ & {S_{\Delta ABC}} = {1 \over 2}AB.AC = {1 \over 2}A{B^2}\sqrt 3 , \cr & {S_{\Delta ABC}}= {1 \over 2}\left( {AB + AC + BC} \right).r \cr&\;\;\;\;\;\;\;\;\;\;\;\,= {1 \over 2}\left( {3 + \sqrt 3 } \right).AB.r. \cr} \)
Từ đó \(AB = \left( {\sqrt 3 + 1} \right)r.\)
Vậy diện tích xung quanh của hình chóp S.ABC là
\(\eqalign{ & {S_2} = {1 \over 2}\left( {3 + \sqrt 3 } \right)AB.SI \cr&\;\;\;\;\;= {1 \over 2}\left( {3 + \sqrt 3 } \right)\left( {\sqrt 3 + 1} \right)r.{r \over {\cos \beta }} \cr & \;\;\;\;\;= {{\sqrt 3 } \over 2}{\left( {\sqrt 3 + 1} \right)^2}{{{r^2}} \over {\cos \beta }}. \cr} \)
Thể tích hình chóp S.ABC là
\({V_2} = {1 \over 3}.{1 \over 2}AB.AC.SO = {{\sqrt 3 } \over 6}A{B^2}.SO,\) từ đó
\(\eqalign{ {V_2} &= {{\sqrt 3 } \over 6}{\left( {\sqrt 3 + 1} \right)^2}{r^2}.r\tan \beta \cr & = {{\sqrt 3 } \over 6}{\left( {\sqrt 3 + 1} \right)^2}{r^3}\tan \beta . \cr} \)
dapandethi.vn
