Đề bài
Trong không gian cho hai hình bình hành \(ABCD\) và \(A’B’C’D’\) chỉ có chung nhau một điểm \(A\). Chứng minh rằng các vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} ,\overrightarrow {DD'} \) đồng phẳng.
Phương pháp giải - Xem chi tiết
Chứng minh rằng \(\overrightarrow {BB'} + \overrightarrow {DD'} = \overrightarrow {CC'} \) suy ra điều phải chứng minh.
Lời giải chi tiết
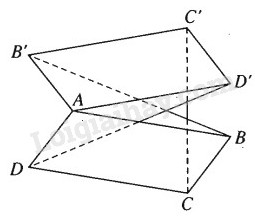
Ta có :
\(\overrightarrow {BB'} = \overrightarrow {BA} + \overrightarrow {AB'} ,\)
\(\overrightarrow {DD'} = \overrightarrow {DA} + \overrightarrow {AD'} \)
Do đó \(\overrightarrow {BB'} + \overrightarrow {DD'} \) \(= \left( {\overrightarrow {BA} + \overrightarrow {DA} } \right) + \left( {\overrightarrow {AB'} + \overrightarrow {AD'} } \right)\)
Vì \(\overrightarrow {BA} = \overrightarrow {C{\rm{D}}} \) và \(\overrightarrow {AB'} + \overrightarrow {AD'} = \overrightarrow {AC'} \)
Nên \(\overrightarrow {BB'} + \overrightarrow {DD'} = \left( {\overrightarrow {C{\rm{D}}} + \overrightarrow {DA} } \right) + \overrightarrow {AC'} \)
Vậy \(\overrightarrow {BB'} + \overrightarrow {DD'} = \overrightarrow {CA} + \overrightarrow {AC'} = \overrightarrow {CC'} \)
Hệ thức \(\overrightarrow {BB'} + \overrightarrow {DD'} = \overrightarrow {CC'} \) biểu thị sự đồng phẳng của ba vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} ,\overrightarrow {DD'} \).
dapandethi.vn
