Đề bài
Tính diện tích hình thoi có cạnh dài \(6\,cm\) và một trong các góc của nó có số đo là \(60^{\circ}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Tam giác đều là tam giác có ba cạnh bằng nhau.
- Định lí Pytago: Bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
- Diện tích hình bình hành bằng tích của một cạnh với chiều cao ứng với cạnh đó.
\(S = ah\)
- Diện tích hình thoi bằng nửa tích độ dài hai đường chéo.
\(S=\dfrac{1}{2}{d_1}.{d_2}\)
Lời giải chi tiết
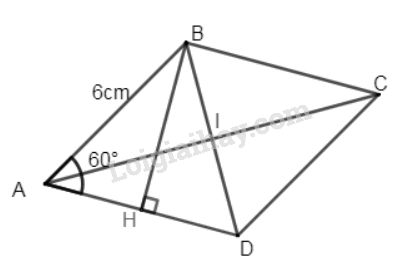
Xét hình thoi \(ABCD\) có cạnh \(6cm\) và \(\widehat {BAD}=60^0\). Kẻ \(BH\bot AD\)
Công thức tổng quát tính độ dài đường cao BH:
Ta có \(∆ABD\) là tam giác đều (vì tam giác \(ABD\) cân có \(\widehat{A}\) = \(60^{\circ}\) )
Tam giác \(ABD\) đều nên đường cao BH cũng là đường trung tuyến hay \(H\) là trung điểm của \(AD\)
Suy ra \(AH=\dfrac{AD}{2}=\dfrac{AB}{2}\)
Áp dụng định lí Pytago vào tam giác vuông \(ABH\) có:
\(B{H^2} = A{B^2} - A{H^2}\)
\( = A{B^2}-\left ( \dfrac{AB}{2} \right )^{2}\)
\( = A{B^2}-\dfrac{AB^{2}}{4} = \dfrac{3AB^{2}}{4}\).
\( \Rightarrow BH = \dfrac{AB.\sqrt{3}}2\) (cm)
Tổng quát: Đường cao tam giác đều cạnh \(a\) có độ dài là: \({h_a}=\dfrac{a\sqrt{3}}2\)
Áp dụng vào bài với cạnh \(a=6cm\) thì \( BH = \dfrac{a.\sqrt{3}}2 = \dfrac{6\sqrt{3}}2 = 3\sqrt3\) (cm)
Tính diện tích hình thoi ABCD.
Cách 1:
Ta có: \( BH = 3\sqrt3\) (cm) (theo trên)
\({S_{ABCD}}= BH. AD = 3\sqrt 3. 6 \)\(\,= 18\sqrt 3\;(c{m^2})\)
Cách 2:
Vì \(∆ABD\) là tam giác đều nên \(BD = AB = 6\,cm\), \(AI\) là đường cao đồng thời là trung tuyến tam giác nên \(AI = \dfrac{6\sqrt{3}}{2} = 3\sqrt3\) (cm)
\(\Rightarrow AC =2AI= 6\sqrt 3\) (cm)
\({S_{ABCD}}=\dfrac{1}{2} BD. AC = \dfrac{1}{2} 6. 6\sqrt 3 \)\(\,= 18\sqrt 3\; (c{m^2})\)
dapandethi.vn
