Đề bài
Cho hình bình hành \(ABCD\). Gọi \(E\) là điểm đối xứng với \(D\) qua điểm \(A\), gọi \(F\) là điểm đối xứng với \(D\) qua điểm \(C\). Chứng minh rằng điểm \(E\) đối xứng với điểm \(F\) qua điểm \(B\).
Phương pháp giải - Xem chi tiết
Áp dụng:
+) Hình bình hành có các cặp cạnh đối song song và bằng nhau.
+) Hai điểm gọi là đối xứng với nhau qua điểm \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó.
+) Tiên đề ơclit: Qua một điểm ở ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Lời giải chi tiết
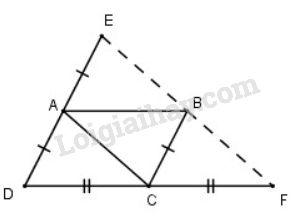

Tứ giác \(ABFC\) có \(AB//CF; \,AB=CF\) (vì cùng bằng \(\dfrac{{DF}}{2}\)) nên là hình bình hành suy ra \(BF//AC\) và \(BF=AC\) (1)
Chứng minh tương tự, tứ giác \(CBEA\) có \(CB//AE; \,CB=AE\) (vì cùng bằng \(\dfrac{{DE}}{2}\)) nên là hình bình hành, suy ra \(BE//AC\) và \(BE=AC\) (2)
Từ (1) và (2) suy ra ba điểm \(E; B; F\) thẳng hàng (theo tiên đề ơclit) và \(BE=BF\).
Vậy điểm \(E\) đối xứng với điểm \(F\) qua điểm \(B\).
Lưu ý: Đừng quên chứng minh ba điểm \(E; B; F\) thẳng hàng.
dapandethi.vn
