Đề bài
Dựng tam giác \(ABC\), biết \(\widehat{A}={60^o}\) và, tỉ số \(\dfrac{AB}{AC} = \dfrac{4}{5}\) và đường cao \(AH = 6cm\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.
- Tính chất hai tam giác đồng dạng.
Lời giải chi tiết
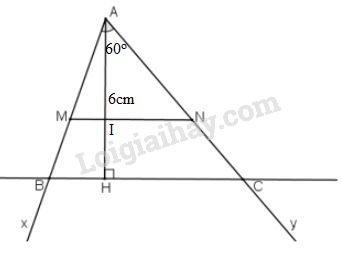
Cách dựng:
- Dựng \(\widehat {xAy} = {60^o}\)
- Trên hai cạnh \(Ax, Ay\) của góc \(\widehat{xAy}\) lần lượt dựng \(AM = 4\,cm\), \(AN = 5\,cm\). Kẻ đường cao \(AI\) của \(∆AMN\).
- Trên tia \(AI\) lấy điểm \(H\) sao cho \(AH = 6\,cm\), qua \(H\) vẽ đường song song với \(MN\) cắt \(Ax, Ay\) lần lượt tại \(B\) và \(C\)
\( \Rightarrow \) \(∆ABC\) thỏa mãn điều kiện bài toán.
Chứng minh:
Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho ta có:
\(MN // BC\) (theo cách dựng)
Suy ra \(∆AMN\) đồng dạng \(∆ABC\).
\( \Rightarrow \dfrac{AM}{AN} = \dfrac{AB}{AC} = \dfrac{4}{5}\) (tính chất hai tam giác đồng dạng)
Vì \(AH ⊥ MN\), mà \(MN//BC\) nên \(AH\bot BC\), \(AH = 6\,cm\) \( \Rightarrow AH\) là đường cao của tam giác \(ABC\).
Vậy tam giác \(ABC\) thỏa mãn yêu cầu bài toán.
dapandethi.vn
