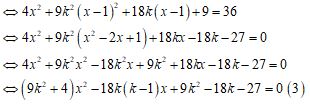Đề bài
Cho elip (E) : \(4{x^2} + 9{y^2} = 36\) và điểm \(M\left( {1;1} \right)\). Viết phương trình đường thẳng \(d\) đi qua \(M\) và cắt \((E)\) tại hai điểm \(A\) và \(B \) sao cho \(M\) là trung điểm của \(AB\).
Phương pháp giải - Xem chi tiết
- Viết dạng phương trình đường thẳng \(d\) đi qua \(M\).
- Xét phương trình hoành độ giao điểm của \(d\) và \(\left( E \right)\).
- Tìm điều kiện để phương trình có hai nghiệm phân biệt và kết luận.
Lời giải chi tiết
\((E)\) : \(4{x^2} + 9{y^2} = 36\). (1)
Xét đường thẳng \(d\) đi qua điểm \(M\left( {1;1} \right)\) và có hệ số góc \(k\).
Ta có phương trình của \(d:y - 1 = k(x - 1)\) hay \(y = k(x - 1) + 1\) (2)
Thay (2) vào (1) ta được \(4x^2 + 9{\left[ {k(x - 1) + 1} \right]^2} = 36\)
Ta có : d cắt (E) tại hai điểm A, B thỏa mãn
MA = MB khi và chỉ khi phương trình (3) có hai nghiệm \({x_A}\), \({x_B}\) sao cho :
\(\dfrac{{{x_A} + {x_B}}}{2} = {x_M}\) \( \Leftrightarrow \dfrac{{ 18k(k-1)}}{{2(9{k^2} + 4)}} = 1\) \( \Leftrightarrow 18{k^2} - 18k = 18{k^2} + 8\) \( \Leftrightarrow k = - \dfrac{4}{9}\).
Vậy phương trình của \(d\) là :
\(y = - \dfrac{4}{9}\left( {x - 1} \right) + 1\) hay \(4x + 9y - 13 = 0.\)
dapandethi.vn