Đề bài
Cho tam giác \(ABC\) có \(a = 20,\,\,b = 16\) và \({m_a} = 10.\) Diện tích của tam giác bằng:
A. \(92.\)
B. \(100.\)
C. \(96.\)
D. \(88.\)
Phương pháp giải - Xem chi tiết
- Tính nửa chu vi \(\Delta AMC\): \(p = \frac{{\frac{a}{2} + {m_a} + b}}{2}\)
- Tính diện tích \(\Delta AMC\): \({S_{\Delta AMC}} = \sqrt {p\left( {p - \frac{a}{2}} \right)\left( {p - {m_a}} \right)\left( {p - b} \right)} \)
- Diện tích \(\Delta ABC\): \(S = 2{S_{\Delta AMC}}\)
Lời giải chi tiết
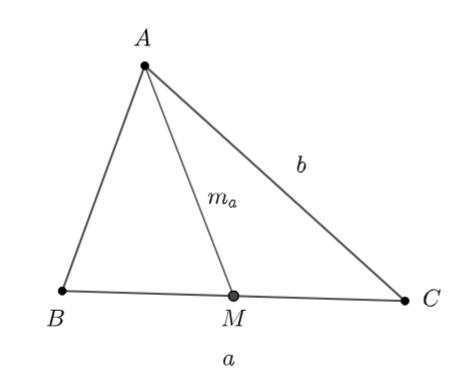
Nửa chu vi \(\Delta AMC\) là: \(p = \frac{{\frac{a}{2} + {m_a} + b}}{2} = \frac{{10 + 10 + 16}}{2} = 18.\)
Diện tích \(\Delta AMC\) là:
\({S_{\Delta AMC}} = \sqrt {p\left( {p - \frac{a}{2}} \right)\left( {p - {m_a}} \right)\left( {p - b} \right)} = \sqrt {18\left( {18 - 10} \right)\left( {18 - 10} \right)\left( {18 - 16} \right)} = 48.\)
Diện tích \(\Delta ABC\) là: \(S = 2{S_{\Delta AMC}} = 2.48 = 96\)
Chọn C.
