Đề bài
Cho tam giác \(ABC\) và \(A'B'C'\) có kích thước như trong hình 35.
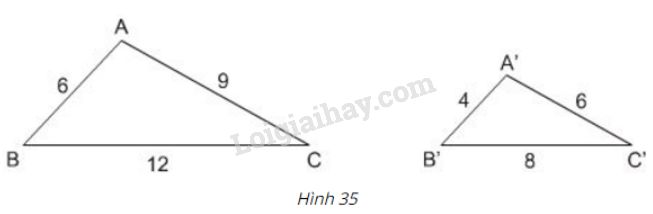
a) Tam giác \(ABC\) và \(A'B'C'\) có đồng dạng với nhau không? Vì sao?
b) Tính tỉ số chu vi của hai tam giác đó.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng:
- Định lí: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
- Tính chất của dãy tỉ số bằng nhau.
- Công thức tính chu vi tam giác.
Lời giải chi tiết
Ta có:
\(\begin{array}{l}
\dfrac{{AB}}{{A'B'}} = \dfrac{6}{4} = \dfrac{3}{2};\,\,\dfrac{{AC}}{{A'C'}} = \dfrac{9}{6} = \dfrac{3}{2};\\\dfrac{{BC}}{{B'C'}} = \dfrac{{12}}{8} = \dfrac{3}{2}\\
\Rightarrow \dfrac{{AB}}{{A'B'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{3}{2}
\end{array}\)
\(\Rightarrow \Delta ABC \text{ đồng dạng }\Delta A'B'C'\) \(\left( c-c-c \right)\)
b) Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{{AB}}{{A'B'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{{BC}}{{B'C'}}\)\(\, = \dfrac{{AB + AC + BC}}{{A'B' + A'C' + B'C'}}\) \( = \dfrac{{{C_{ABC}}}}{{{C_{A'B'C'}}}} = \dfrac{3}{2}\)
(với \(C_{ABC}\) và \(C_{A'B'C'}\) lần lượt là chu vi của hai tam giác \(ABC, A'B'C')\)
Vậy tỉ số chu vi của tam giác ABC và chu vi của tam giác A’B’C’ là \(\dfrac{3}{2}\)
dapandethi.vn
