Đề bài
Cho tam giác \(ABC\) vuông tại \(A\), \(AB = a\), \(BC = 2a\). Tích vô hướng \(\overrightarrow {BA} .\overrightarrow {BC} \) bằng
A. \({a^2}\) B. \( - {a^2}\)
C. \(\dfrac{1}{2}{a^2}\) D. \({a^2}\sqrt 3 \)
Phương pháp giải - Xem chi tiết
Tính \(\cos B\) và áp dụng công thức \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\) tính tích vô hướng.
Lời giải chi tiết
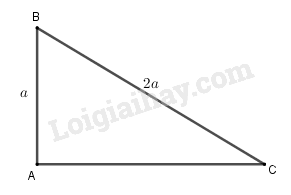
Ta có: \(\Delta ABC\) vuông tại \(A\) nên \(\cos B = \dfrac{{AB}}{{BC}} = \dfrac{a}{{2a}} = \dfrac{1}{2}\)
\(\overrightarrow {BA} .\overrightarrow {BC} \)\( = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right)\) \( = a.2a.\dfrac{1}{2} = {a^2}\).
Chọn A.
Cách khác:
\(\begin{array}{l}
\overrightarrow {BA} .\overrightarrow {BC} = - \overrightarrow {AB} \left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)\\
= - \overrightarrow {AB} .\overrightarrow {AC} + {\overrightarrow {AB} ^2}\\
= 0 + A{B^2}\\
= 0 + {a^2}\\
= {a^2}
\end{array}\)
dapandethi.vn
