Đề bài
Cho tam giác \(ABC\) vẽ tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\) theo tỉ số đồng dạng là \(k = \dfrac{2}{3}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.
Lời giải chi tiết
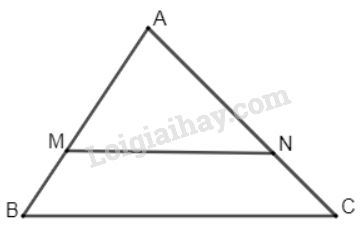
Trên cạnh \(AB\) lấy điểm \(M\) sao cho \(AM= \dfrac{2}{3}AB.\)
Từ \(M\) kẻ đường song song với \(BC\) cắt \(AC\) tại \(N\).
Ta có \(∆AMN\) ∽ \(∆ABC\) theo tỉ số đồng dạng \(k=\dfrac{AM}{AB}=\dfrac{2}{3}\)
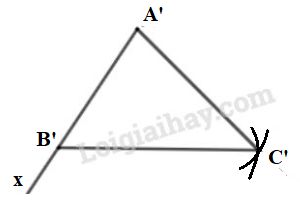
*) Dựng \(∆A'B'C' = ∆AMN\) (theo trường hợp cạnh cạnh cạnh)
- Dựng tia \(A’x\), trên tia \(A’x\) lấy \(B’\) sao cho \(A’B’ = AM\)
- Dựng cung tròn tâm \(A’\) bán kính \(AN\) và cung tròn tâm \(B’\) bán kính \(MN\), hai cung tròn cắt nhau tại \(C’\)
- Nối \(A'C', B'C'\) ta được tam giác \(A'B'C'\) phải dựng.
Mà \(∆AMN\) ∽ \(∆ABC\) theo tỉ số đồng dạng \(k=\dfrac{2}{3}\) nên \(∆A'B'C'\) ∽ \(∆ABC\) theo tỉ số đồng dạng \(k=\dfrac{2}{3}\).
dapandethi.vn
