Cho phương trình \(\displaystyle {1 \over 2}{x^2} - 2x + 1 = 0\)
LG a
Vẽ đồ thị của hàm số \(\displaystyle y = {1 \over 2}{x^2}\) và \(y = 2x - 1\) trên cùng một mặt phẳng tọa độ. Dùng đồ thị tìm giá trị gần đúng nghiệm của phương trình (làm tròn đến chữ số thập phân thứ hai).
Phương pháp giải:
- Lập bảng giá trị \(x,y\) của hàm số \(\displaystyle y = {1 \over 2}{x^2}\) từ đó vẽ đồ thị của hàm số đó.
- Lấy hai điểm phân biệt thuộc đồ thị hàm số \(y = 2x - 1\), đường thẳng đi qua hai điểm đó là đồ thị của hàm số \(y = 2x - 1\).
* Từ các giao điểm trên đồ thị ta dựng đường thẳng vuông góc với trục hoành cắt trục hoành tại đâu thì đó là hoành độ giao điểm của hai đồ thị đã cho.
Lời giải chi tiết:
* Vẽ đồ thị \(\displaystyle y = {1 \over 2}{x^2}\)
|
x |
-2 |
-1 |
0 |
1 |
2 |
| \(y =\displaystyle {1 \over 2}{x^2}\) |
2 |
\(\dfrac{1}{2}\) |
0 |
\(\dfrac{1}{2}\) |
2 |
* Vẽ đồ thị \(y = 2x - 1\)
- Cho \(x = 0 ⇒ y = -1\) ta được \(A (0; -1)\) thuộc đồ thị của hàm số \(y = 2x - 1\).
- Cho \(y=0 \Rightarrow x = \dfrac{1}{2}\) ta được \(B\left( {\dfrac{1}{2};0} \right)\) thuộc đồ thị của hàm số \(y = 2x - 1\).
Vậy đường thẳng \(AB\) là đồ thị của hàm số \(y = 2x - 1\).
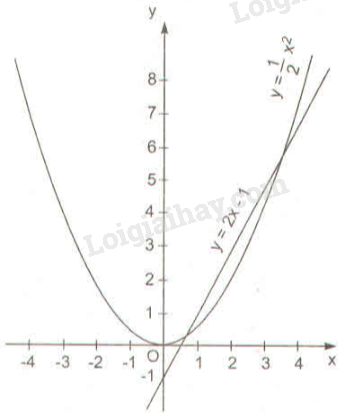
Từ đồ thị ta dự đoán:
Hoành độ giao điểm là: \({x_1} \approx 0,60;{x_2} \approx 3,40\).
Nghiệm của phương trình là: \({x_1} \approx 0,60;{x_2} \approx 3,40\).
LG b
Giải phương trình đã cho bằng công thức nghiệm, so sánh với kết quả tìm được trong câu a.
Phương pháp giải:
Phương trình \(a{x^2} + bx + c = 0(a \ne 0)\) và biệt thức \(\Delta = {b^2} - 4ac\):
+) Nếu \(\Delta > 0\) thì phương trình có hai nghiệm phân biệt:
\({x_1}\)= \(\dfrac{-b + \sqrt{\bigtriangleup }}{2a}\) và \({x_2}\)= \(\dfrac{-b - \sqrt{\bigtriangleup }}{2a}\)
+) Nếu \(\Delta = 0\) thì phương trình có nghiệm kép \({x_1}={x_2}=\dfrac{-b }{2a}\).
+) Nếu \(\Delta < 0\) thì phương trình vô nghiệm.
Lời giải chi tiết:
\(\displaystyle {1 \over 2}{x^2} - 2x + 1 = 0\)
\( \Leftrightarrow {x^2} - 4x + 2 = 0 \)
\( \Delta = {\left( { - 4} \right)^2} - 4.1.2 = 16 - 8 = 8 > 0 \)
\( \Rightarrow \sqrt \Delta = \sqrt 8 = 2\sqrt 2 \)
Phương trình có hai nghiệm phân biệt là:
\( {x_1} = \dfrac{{ - b + \sqrt \Delta }}{{2a}}\)\( \displaystyle = {{4 + 2\sqrt 2 } \over {2.1}} = 2 + \sqrt 2 \approx 3,41 \)
\(\displaystyle {x_2}= \dfrac{{ - b - \sqrt \Delta }}{{2a}}\)\( \displaystyle = {{4 - 2\sqrt 2 } \over {2.1}} = 2 - \sqrt 2 \approx 0,59 \).
Hai nghiệm của phương trình là \({x_1} \approx 0,59;{x_2} \approx 3,41\) gần giống với kết quả tìm được ở câu b.
dapandethi.vn
