Đề bài
Tam giác ABC vuông tại A và có \(AB = AC = a\). Tính:
a) \(\overrightarrow {AB} .\overrightarrow {AC} \);
b) \(\overrightarrow {BA} .\overrightarrow {BC} \)
c) \(\overrightarrow {AB} .\overrightarrow {BC} \).
Phương pháp giải - Xem chi tiết
Sử dụng công thức tích vô hướng của hai véc tơ \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos (\overrightarrow a ,\overrightarrow b )\).
Lời giải chi tiết
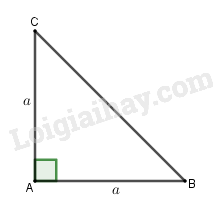
a) \(\overrightarrow {AB} .\overrightarrow {AC} = 0\) vì \(AB \bot AC\).
b) \(\overrightarrow {BA} .\overrightarrow {BC} \)\( = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right)\) \( = a.a\sqrt 2 .\cos {45^0} = {a^2}\)
c) \(\overrightarrow {AB} .\overrightarrow {BC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right)\)\( = a.a\sqrt 2 .\cos {135^0} = - {a^2}\)
dapandethi.vn
