Tìm giá trị của m:
LG a
Để hai đường thẳng\(({d_1})\):\(5x - 2y = 3,\) \(({d_2})\): \(x + y = m\) cắt nhau tại một điểm trên trục \(Oy\). Vẽ hai đường thẳng này trong cùng một mặt phẳng tọa độ.
Phương pháp giải:
Sử dụng:
- Hai đường thẳng cắt nhau tại một điểm \(A\) trên trục \(Oy\) thì \(A(0;y).\)
- Hai đường thẳng \(({d_1})\): \(ax + by = c\) và \(({d_2})\): \(a'x+b'y = c'\) cắt nhau tại điểm \(M({x_0};{y_0})\) thì tọa độ của \(M\) là nghiệm của hệ phương trình: \(\left\{ {\matrix{
{ax + by = c} \cr
{a'x+b'y = c'} \cr} } \right.\)
- Cặp số \(({x_0};{y_0})\) là nghiệm của hệ phương trình
\(\left\{ {\matrix{
{ax + by = c} \cr
{a'x +b'y = c'} \cr} } \right.\)
\( \Leftrightarrow \left\{ {\matrix{
{a{x_0} + b{y_0} = c} \cr
{a'{x_0} +b'{y_0} = c'} \cr} } \right.\)
Lời giải chi tiết:
Vì đường thẳng \(({d_1})\): \(5x - 2y = 3,\)
\(({d_2})\): \(x + y = m\) cắt nhau tại một điểm trên trục \(Oy\) nên giao điểm \(A\) của \(({d_1})\) và \(({d_2})\) có hoành độ bằng \(0\), giả sử \(A(0; y).\)
Khi đó \(A(0; y)\) là nghiệm của hệ phương trình:\(\left\{ {\matrix{
{5x - 2y = 3} \cr
{x + y = m} \cr} } \right.\)
Thay toạ độ điểm \(A\) vào hệ phương trình trên ta được:
\(\left\{ {\matrix{
{5.0 - 2y = 3} \cr
{0 + y = m} \cr} } \right. \Leftrightarrow \left\{ {\matrix{
{y = \displaystyle - {3 \over 2}} \cr
{m = \displaystyle - {3 \over 2}} \cr} } \right.\)
Vậy \(m = \displaystyle - {3 \over 2}\) thì \(({d_1})\) cắt \(({d_2})\) tại một điểm trên trục tung.
- Với \(m = \displaystyle - {3 \over 2}\) ta có \(({d_2})\): \(x + y = \displaystyle - {3 \over 2} \)\( \Leftrightarrow y = -x \displaystyle - {3 \over 2}\)
Cho \(x = 0 \Rightarrow y = \displaystyle- {3 \over 2}\) ta được \(M \displaystyle \left( {0; - {3 \over 2}} \right)\)
Cho \(y = 0 \Rightarrow x = \displaystyle - {3 \over 2}\) ta được \(N \displaystyle\left( { - {3 \over 2};0} \right)\)
Đường thẳng \(({d_2})\) là đường thẳng đi qua hai điểm \(M, \ N\).
- Vẽ \(({d_1})\): \(5x - 2y = 3 \Leftrightarrow y = \displaystyle {5\over 2}x - \displaystyle {3 \over 2}\)
Cho \(x = 0 \Rightarrow y = \displaystyle - {3 \over 2}\) ta được \(M\displaystyle \left( {0; - {3 \over 2}} \right)\)
Cho \(y = 0 \Rightarrow x = \displaystyle {3 \over 5}\) ta được \(P\displaystyle \left( {{3 \over 5};0} \right)\)
Đường thẳng \(({d_1})\) là đường thẳng đi qua hai điểm \(M, \ P\).

LG b
Để hai đường thẳng \(({d_1})\): \(mx + 3y = 10\), \(({d_2})\): \(x - 2y = 4\) cắt nhau tại một điểm trên trục \(Ox\). Vẽ hai đường thẳng này trong cùng một mặt phẳng tọa độ.
Phương pháp giải:
Sử dụng:
- Hai đường thẳng cắt nhau tại một điểm \(A\) trên trục \(Oy\) thì \(A(0;y).\)
- Hai đường thẳng \(({d_1})\): \(ax + by = c\) và \(({d_2})\): \(a'x+b'y = c'\) cắt nhau tại điểm \(M({x_0};{y_0})\) thì tọa độ của \(M\) là nghiệm của hệ phương trình: \(\left\{ {\matrix{
{ax + by = c} \cr
{a'x+b'y = c'} \cr} } \right.\)
- Cặp số \(({x_0};{y_0})\) là nghiệm của hệ phương trình
\(\left\{ {\matrix{
{ax + by = c} \cr
{a'x +b'y = c'} \cr} } \right.\)
\( \Leftrightarrow \left\{ {\matrix{
{a{x_0} + b{y_0} = c} \cr
{a'{x_0} +b'{y_0} = c'} \cr} } \right.\)
Lời giải chi tiết:
Vì đường thẳng \(({d_1})\): \(mx + 3y = 10\) và đường thẳng \(({d_2})\): \(x – 2y = 4\) cắt nhau tại một điểm trên trục hoành nên giao điểm \(B\) của \(({d_1})\) và \(({d_2})\) có tung độ bằng \(0\), giả sử \(B(x; 0)\)
Khi đó \(B(x; 0)\) là nghiệm của hệ phương trình:\(\left\{ {\matrix{
{mx + 3y = 10} \cr
{x – 2y = 4} \cr} } \right.\)
Thay toạ độ điểm \(B\) vào hệ phương trình trên ta được:
\(\eqalign{
& \left\{ {\matrix{
{mx + 3.0 = 10} \cr
{x - 2.0 = 4} \cr} } \right. \Leftrightarrow \left\{ {\matrix{
{mx = 10} \cr
{x = 4} \cr} } \right. \cr
& \Leftrightarrow \left\{ {\matrix{
{m = \displaystyle {10 \over x}} \cr
{x = 4} \cr} } \right.\cr
& \Leftrightarrow \left\{ {\matrix{
{m = \displaystyle {5 \over 2}} \cr
{x = 4} \cr} } \right. \cr} \)
Vậy \(m = \displaystyle {5 \over 2}\) thì \(({d_1})\) cắt \(({d_2})\) tại một điểm trên trục hoành.
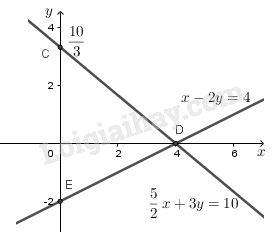
- Với \(m = \displaystyle {5 \over 2}\) ta có \(({d_1})\): \(\displaystyle {5 \over 2}x + 3y = 10\)\(\Leftrightarrow y = \displaystyle - {5 \over 6}x+\displaystyle {10 \over 3}\)
Cho \(x = 0 \Rightarrow y = \displaystyle {{10} \over 3}\) ta được \(C\displaystyle \left( {0;{{10} \over 3}} \right)\)
Cho \(y = 0 \Rightarrow x = 4\) ta được \(D\left( {4;0} \right)\)
Đường thẳng \(({d_1})\) là đường thẳng đi qua hai điểm \(C, \ D\).
- Vẽ \(\left( {{d_2}} \right):x - 2y = 4 \Leftrightarrow y= \displaystyle {1 \over 2}x-2\)
Cho \(x = 0 \Rightarrow y = - 2\) ta được \(E\left( {0; - 2} \right)\)
Cho \(y = 0 \Rightarrow x = 4\) ta được \(D\left( {4;0} \right)\).
Đường thẳng \(({d_2})\) là đường thẳng đi qua hai điểm \(E,\ D\).
dapandethi.vn
