Đề bài
Cho tam giác đều \(ABC\) nội tiếp đường tròn \((O)\) và \(M\) là một điểm của cung nhỏ \(BC.\) Trên \(MA\) lấy điểm \(D\) sao cho \(MD = MB.\)
\(a)\) Hỏi tam giác MBD là tam giác gì\(?\)
\(b)\) So sánh hai tam giác \(BDA\) và \(BMC.\)
\(c)\) Chứng minh rằng \(MA = MB + MC.\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải chi tiết
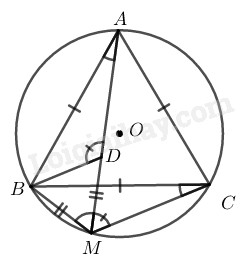
\(a)\) \(MB = MD \;\;(gt)\) \( \Rightarrow \) \(∆MBD\) cân tại \(M\)
\(\widehat {AMB} = \widehat {ACB}\) (\(2\) góc nội tiếp cùng chắn cung \(\overparen{AB}\))
Mà \(\widehat {ACB} = {60^0}\) (vì \(∆ABC\) đều)
\( \Rightarrow \widehat {AMB} = {60^0}\) hay \(\widehat {DMB} = {60^0}\)
Vậy \(∆MBD\) đều
\(b)\) \(∆MBD\) đều
\( \Rightarrow \widehat {DBC} + \widehat {CBM} = \widehat {DBM} = {60^0}\) \( (1)\)
\(∆ABC\) đều \( \Rightarrow \widehat {ABD} + \widehat {DBC} = \widehat {ABC} = {60^0}\) \( (2)\)
Từ \((1)\) và \((2)\) suy ra: \(\widehat {CBM} = \widehat {ABD}\)
Xét \(∆BDA\) và \(∆BMC:\)
\(BA = BC \;\;(gt)\)
\(\widehat {ABD} = \widehat {CBM}\) (chứng minh trên)
\(BD = BM\) (vì \(∆MBD\) đều)
Suy ra: \(∆BDA = ∆BMC\;\; (c.g.c)\)
\(c)\) \(∆BDA = ∆BMC\) (chứng minh trên)
\( \Rightarrow DA = MC\)
Ta có: \(MB = MD\;\; (gt)\) mà \(AM = AD + DM\)
Suy ra: \(MA = MB + MC \;\;(đpcm)\)
dapandethi.vn
