Đề bài
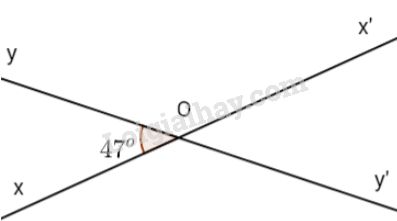
Vẽ hai đường thẳng cắt nhau sao cho trong các góc tạo thành có một góc \(47^{\circ}\). Tính số đo các góc còn lại.
Phương pháp giải - Xem chi tiết
- Hai góc đối đỉnh thì bằng nhau
- Tổng số đo hai góc kề bù bằng \(180^o\).
Lời giải chi tiết
Học sinh vẽ hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) sao cho \(\widehat{xOy}=47^{\circ}\) rồi suy luận như sau:
\(\widehat{xOy'}=180^{\circ}-\widehat{xOy}=180^{\circ}-47^{\circ}\)\(=133^{\circ}\) (vì \(\widehat{xOy}\) và \(\widehat{xOy'}\) là hai góc kề bù)
\(\widehat{x'Oy'}=\widehat{xOy}=47^{\circ}\) (vì là hai góc đối đỉnh).
\(\widehat{x'Oy}=\widehat{xOy'}=133^{\circ}\) (vì là hai góc đối đỉnh).
dapandethi.vn
