Đề bài
Cho đường tròn (O), đường kính \(AD = 2R\). Vẽ cung tâm \(D\) bán kính \(R\), cung này cắt đường tròn (O) ở \(B\) và \(C.\)
a) Tứ giác \(OBDC\) là hình gì? Vì sao?
b) Tính số đo các góc \(CBD, CBO, OBA.\)
c) Chứng minh rằng tam giác \(ABC\) là tam giác đều.
Phương pháp giải - Xem chi tiết
+ Tứ giác có tất cả các cạnh bằng nhau thì tứ giác đó là hình thoi.
+ Tam giác cân có một góc bằng \(60^\circ \) là tam giác đều.
Lời giải chi tiết
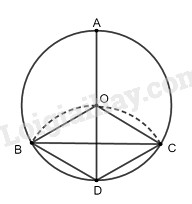
a) Ta có:
\(OB = OC = R\) (vì \(B, C\) nằm trên \((O ; R))\)
\(DB = DC = R\) ( vì \(B, C\) nằm trên \((D ; R))\)
Suy ra: \(OB = OC = DB = DC.\)
Vậy tứ giác \(OBDC\) là hình thoi.
b) Ta có: \(OB = OD = BD = R\)
\(∆OBD\) đều \( \Rightarrow \widehat {OBD} = 60^\circ \)
Vì \(OBDC\) là hình thoi nên:
\(\widehat {CBD} = \widehat {OBC} = \dfrac{1 }{ 2}\widehat {OBD} = 30^\circ \)
Tam giác \(ABD\) nội tiếp trong (O) có \(AD\) là đường kính nên:
\(\widehat {ABD} = 90^\circ \)
Suy ra \(\widehat {OBD} + \widehat {OBA} = 90^\circ \)
Nên \(\widehat {OBA} = \widehat {ABD} - \widehat {OBD}\)\( = 90^\circ - 60^\circ = 30^\circ \)
c) Tứ giác \(OBDC\) là hình thoi nên \(OD ⊥ BC\) hay \(AD ⊥ BC\)
Suy ra AD là đường trung trực của BC (vì O là tâm đường tròn ngoại tiếp tam giác ABC và \(O\in AD\))
Ta có:
\(AB = AC\) ( tính chất đường trung trực)
Suy ra tam giác \(ABC\) cân tại \(A\) (1)
Mà \(\widehat {ABC} = \widehat {OBC} + \widehat {OBA} \)\(= 30^\circ + 30^\circ = 60^\circ \). (2)
Từ (1) và (2) suy ra tam giác \(ABC\) đều.
dapandethi.vn
