Một hình chóp với tứ giác đều ngoại tiếp hình cầu bán kính a
LG a
Chứng minh rằng thể tích của hình chóp là
\(V = {{4{a^2}{x^2}} \over {3(x - 2a)}}.\)
Trong đó x là chiều cao của hình chóp.
Phương pháp giải:
Mặt phẳng đi qua đường cao SH của hình chóp và trung điểm M của một cạnh đáy cắt hình chóp theo tam giác cân SMN và cắt hình cầu theo tâm O bán kính a nội tiếp tam giác SMN.
Có thể tính thể tích hình chóp theo x và \(\alpha = \widehat {SNH}\).
Sau đó sử dụng đẳng thức \(x = a + {\rm{OS}}\) để tìm hệ thức giữa a, x và \(\alpha \).
Lời giải chi tiết:
Mặt phẳng đi qua đường cao SH của hình chóp và trung điểm M của một cạnh đáy cắt hình chóp theo tam giác cân SMN và cắt hình cầu theo tâm O bán kính a nội tiếp tam giác SMN.
Ta có \(HN = x\cot \alpha ;MN = 2x\cot \alpha \).
Thể tích hình chóp là \(V = {1 \over 3}M{N^2}.SH = {4 \over 3}{x^3}{\cot ^2}\alpha \)
Ta tính \({\cot ^2}\alpha \) theo a và x.
Từ đẳng thức SH = OH + OS ta có \(x = a + {a \over {{\rm{cos }}\alpha }}\); do đó \({\rm{cos }}\alpha = {a \over {x - a}}\)
\({\sin ^2}\alpha = 1 - c{\rm{o}}{{\rm{s}}^2}\alpha \)
\(= 1 - {{{a^2}} \over {{{\left( {x - a} \right)}^2}}} = {{{x^2} - 2ax} \over {{{\left( {x - a} \right)}^2}}}\)
\({\cot ^2}\alpha = {{c{\rm{o}}{{\rm{s}}^2}\alpha } \over {{{\sin }^2}\alpha }} = {{{a^2}} \over {x{{\left( {x - 2a} \right)}^2}}}\)
Từ đó suy ra công thức cần chứng minh.
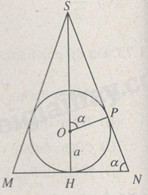
LG b
Với giá trị nào của x,hình chóp có thể tích là nhỏ nhất ?
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}V\left( x \right) = \frac{{4{a^2}{x^2}}}{{3\left( {x - 2a} \right)}}\\V'\left( x \right) = \frac{4}{3}.\frac{{2{a^2}x\left( {x - 2a} \right) - {a^2}{x^2}}}{{{{\left( {x - 2a} \right)}^2}}}\\ = \frac{4}{3}.\frac{{{a^2}{x^2} - 4{a^3}x}}{{{{\left( {x - 2a} \right)}^2}}}\\V'\left( x \right) = 0 \Leftrightarrow {a^2}{x^2} - 4{a^3}x = 0\\ \Leftrightarrow {a^2}x\left( {x - 4a} \right) = 0\\ \Leftrightarrow x = 4a\left( {do\,x > 2a} \right)\end{array}\)
Lập BBT suy ra hàm số \(V\left( x \right)\) đạt GTNN tại \(x = 4a\).
dapandethi.vn
