Đề bài
Cho hình bình hành \(ABCD\). Gọi \(E\) và \(F \) lần lượt là trung điểm của hai cạnh \(AB\) và \(CD\). Nối \(AF\) và \(CE\), hai đường thẳng này cắt đường chéo \(BD\) lần lượt tại \(M\) và \(N\). Chứng minh \(\overrightarrow {DM} = \overrightarrow {MN} = \overrightarrow {NB} \).
Phương pháp giải - Xem chi tiết
Hai véc tơ bằng nhau nếu chúng cùng hướng và cùng độ dài.
Lời giải chi tiết
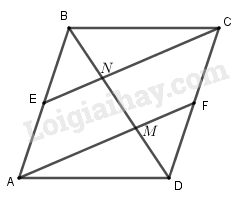
\(AECF\) là hình bình hành \( \Rightarrow \) \(EN // AM\)
\(E\) là trung điểm của \(AB\) \( \Rightarrow \) \(N\) là trung điểm của \(BM\), do đó \(MN = NB\).
Tương tự, \(M\) là trung điểm của \(DN\), do đó \(DM = MN\).
Vậy \(\overrightarrow {DM} = \overrightarrow {MN} = \overrightarrow {NB} \).
dapandethi.vn
