LG a
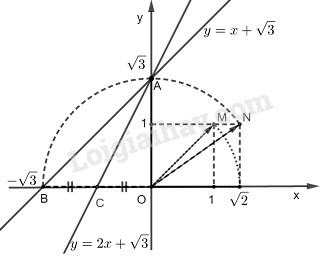
Vẽ đồ thị của các hàm số sau trên cũng một mặt phẳng tọa độ:
\(y = x + \sqrt 3\); (1)
\(y = 2x + \sqrt 3 \); (2)
Phương pháp giải:
Cách vẽ đồ thị hàm số \(y = ax + b\) \((a \ne 0)\)
+ Nếu \(b = 0\) ta có hàm số \(y = ax\) . Đồ thị của \(y = ax\) là đường thẳng đi qua gốc tọa độ \(O(0;0)\) và điểm \(A(1;a)\);
+ Nếu \(b \ne 0\) thì đồ thị \(y = ax + b\) là đường thẳng đi qua các điểm \(A(0;b)\); \(B( - \dfrac{b}{a};0)\).
Lời giải chi tiết:
*) Vẽ đồ thị của hàm số \(y = x + \sqrt 3 \)
Cho x = 0 thì \(y = \sqrt 3 \). Ta có: \(A\left( {0;\sqrt 3 } \right)\)
Cho y = 0 thì \(x + \sqrt 3 = 0 \Rightarrow x = - \sqrt 3 \). Ta có: \(B\left( { - \sqrt 3 ;0} \right)\)
*) Cách tìm điểm có tung độ bằng \(\sqrt 3 \) trên trục Oy:
- Dựng điểm M(1;1). Ta có: \(OM =\sqrt{1^2+1^2}= \sqrt 2 \)
- Dựng cung tròn tâm O bán kính OM cắt trục Ox tại điểm có hoành độ bằng \(\sqrt 2 \) .
- Dựng điểm \(N\left( {1;\sqrt 2 } \right)\). Ta có: \(ON =\sqrt {1^2+(\sqrt 2)^2}= \sqrt 3 \)
- Vẽ cung tròn tâm O bán kính ON cắt trục Oy tại A có tung độ \(\sqrt 3 \) cắt tia đối của Ox tại B có hoành độ \(-\sqrt 3 \) .
Đồ thị của hàm số \(y = x + \sqrt 3 \) là đường thẳng AB.
*) Vẽ đồ thị của hàm số \(y = 2x + \sqrt 3 \)
Cho x = 0 thì \(y = \sqrt 3 \). Ta có: \(A\left( {0;\sqrt 3 } \right)\)
Cho y = 0 thì \(2x + \sqrt 3 = 0 \Rightarrow x = - \dfrac{{\sqrt 3 }}{2}\). Ta có: \(C\left( { - \dfrac{{\sqrt 3 } }{2};0} \right)\)
Đồ thị của hàm số \(y = 2x + \sqrt 3 \) là đường thẳng AC
LG b
Gọi giao điểm của đường thẳng \(y = x + \sqrt 3 \) với các trục Oy, Ox theo thứ tự là A, B và giao điểm của đường thẳng \(y = 2x + \sqrt 3 \) với các trục Oy, Ox theo thứ tự là A, C. Tính các góc của tam giác ABC (dùng máy tính bỏ túi CASIO fx-220 hoặc CASIO fx-500A).
Phương pháp giải:
Sử dụng định nghĩa tỉ số lượng giác của góc nhọn
Sử dụng định lý tổng ba góc trong tam giác bằng \(180^0\)
Lời giải chi tiết:
Xét tam giác \(ABO\) vuông tại \(O\), có: \(tg\widehat {ABO} = \dfrac{{OA}}{{OB}} = \dfrac{{\sqrt 3 }}{{\sqrt 3 }} = 1\)\( \Rightarrow \widehat {ABO} = {45^0}\) hay \(\widehat {ABC} = {45^0}\)
Xét tam giác \(ACO\) vuông tại \(O\), có: \(tg\widehat {ACO} = \dfrac{{OA}}{{OC}} = \dfrac{{\sqrt 3 }}{{\dfrac{{\sqrt 3 }}{ 2}}} = 2\)\( \Rightarrow \widehat {ACO} = {63^0}26'\)
Ta có: \(\widehat {ACO} + \widehat {ACB} = {180^0}\) (hai góc kề bù)
Suy ra : \(\widehat {ACB} = {180^0} - \widehat {ACO}\)\( = {180^0} - {63^0}26' = {116^0}34'\)
Lại có: \(\widehat {ACB} + \widehat {ABC} + \widehat {BAC} = {180^0}\) (tổng ba góc trong tam giác \(ABC\))
Suy ra:
\(\eqalign{
& \widehat {BAC} = {180^0} - \left( {\widehat {ACB} + \widehat {ABC}} \right) \cr
& = {180^0} - \left( {{{45}^0} + {{116}^0}34'} \right) = {18^0}26' \cr} \)
dapandethi.vn
