Đề bài
Cho tam giác \(ABC\) vuông tại \(A\), \(\widehat B = 60^\circ \) và \(BC = 2a\) (đơn vị độ dài). Quay tam giác đó một vòng quanh cạnh huyền \(BC\). Hãy tính diện tích xung quanh và thể tích của hình tạo thành.
Phương pháp giải - Xem chi tiết
Sử dụng:
- Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\).
- Thể tích hình nón: \(\displaystyle V = {1 \over 3}\pi {r^2}h\).
(\(r\) là bán kính đường tròn đáy, \( l\) là đường sinh, \(h\) là chiều cao).
Lời giải chi tiết
Khi quay tam giác vuông \(ABC\) một vòng xung quanh cạnh huyền \(BC\) ta thu được hai hình nón có đáy úp vào nhau, bán kính đường tròn đáy bằng đường cao \(AH\) kẻ từ \(A\) đến cạnh huyền \(BC\).
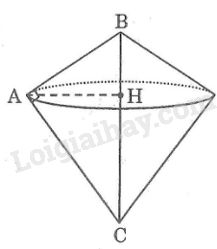
Trong tam giác vuông \(ABC\) ta có:
+) \( AB = BC. \cos B = 2a. \cos60^o\)\(\,\displaystyle= 2a.{1 \over 2} = a\)
+) \(AC = BC. \sin B = 2a. \sin60^o\)\(\,\displaystyle =2a.{{\sqrt 3 } \over 2} = a\sqrt 3 \)
+) \(AB.AC=AH.BC\) (hệ thức lượng trong tam giác vuông)
\(\Rightarrow AH =\displaystyle {{AB.AC} \over {BC}} = {{a.a\sqrt 3 } \over {2a}} = {{a\sqrt 3 } \over 2}\)
Diện tích xung quanh hình tạo thành là:
\(S = π. AH. AB + π AH. AC\)\(= π. AH. (AB+AC)\)
\(\displaystyle = \pi .{{a\sqrt 3 } \over 2}(a + a\sqrt 3 ) \)\(\,\displaystyle = {{\pi {a^2}(3 + \sqrt 3 )} \over 2}\) (đơn vị diện tích)
Thể tích hình tạo thành là:
\(V = \displaystyle{1 \over 3}\pi A{H^2}.BH + {1 \over 3}\pi A{H^2}.HC\)\(\,\displaystyle = {1 \over 3}\pi A{H^2}.(BH + HC)\)
\(V = \displaystyle {1 \over 3}\pi A{H^2}.BC = {1 \over 3}\pi {\left( {{{a\sqrt 3 } \over 2}} \right)^2}.2a \)\(\,\displaystyle= {1 \over 3}\pi. {{{a^2}.3} \over 4}.2a = {{\pi {a^3}} \over 2} \).
dapandethi.vn
