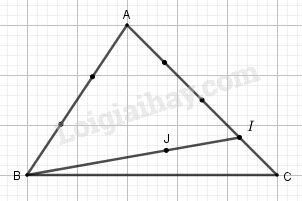
Cho tam giác \(ABC\). Điểm \(I\) trên cạnh \(AC\) sao cho \(CI = \dfrac{1}{4}CA\), \(J\) là điểm mà \(\overrightarrow {BJ} = \dfrac{1}{2}\overrightarrow {AC} - \dfrac{2}{3}\overrightarrow {AB} \).
LG a
Chứng minh \(\overrightarrow {BI} = \dfrac{3}{4}\overrightarrow {AC} - \overrightarrow {AB} \).
Phương pháp giải:
Xen điểm và biểu diễn các véc tơ thích hợp.
Lời giải chi tiết:
\(\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {AI} = - \overrightarrow {AB} + \dfrac{3}{4}\overrightarrow {AC} \)
LG b
Chứng minh \(B, I, J\) thẳng hàng.
Phương pháp giải:
Chứng minh \(\overrightarrow {BJ} = k\overrightarrow {BI} \).
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}
\overrightarrow {BJ} = \frac{1}{2}\overrightarrow {AC} - \frac{2}{3}\overrightarrow {AB} \\
\overrightarrow {BI} = \frac{3}{4}\overrightarrow {AC} - \overrightarrow {AB} \\
\Rightarrow \frac{2}{3}\overrightarrow {BI} = \frac{2}{3}\left( {\frac{3}{4}\overrightarrow {AC} - \overrightarrow {AB} } \right)\\
= \frac{1}{2}\overrightarrow {AC} - \frac{2}{3}\overrightarrow {AB} = \overrightarrow {BJ} \\
\Rightarrow \overrightarrow {BJ} = \frac{2}{3}\overrightarrow {BI}
\end{array}\)
Vậy ba điểm \(B, J, I\) thẳng hàng.
LG c
Hãy dựng điểm \(J\) thỏa mãn điều kiện đề bài.
Phương pháp giải:
Dựng hình dựa vào ý b.
Lời giải chi tiết:
Do \(\overrightarrow {BJ} = \dfrac{2}{3}\overrightarrow {BI} \) nên ta dựng được hình như hình vẽ trên.
dapandethi.vn
