Đề bài
Cho hình thang cân \(ABCD \;( AB // CD, AB < CD).\) Kẻ đường cao \(AE, BF\) của hình thang. Chứng minh rằng \(DE = CF.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Tính chất hình thang cân: hình thang cân có hai cạnh bên bằng nhau, hai góc kề \(1\) đáy bằng nhau.
+) Dấu hiệu nhận biết hai tam giác vuông bằng nhau: Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
+) Tính chất hai tam giác bằng nhau: hai cạnh tương ứng bằng nhau.
Lời giải chi tiết
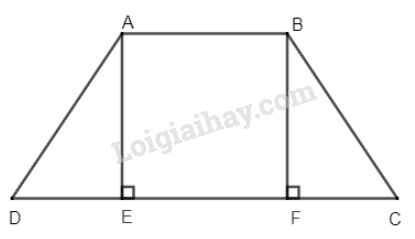
Vì \(ABCD\) là hình thang cân (giả thiết)
\( \Rightarrow \left\{ \begin{array}{l}
A{\rm{D}} = BC\\
\widehat D = \widehat C
\end{array} \right.\) (tính chất hình thang cân)
Xét hai tam giác vuông \(AED\) và \(BFC\) có:
+) \(AD = BC\) (chứng minh trên)
+) \(\widehat D = \widehat C\) (chứng minh trên)
Suy ra \( ∆AED = ∆BFC\) (cạnh huyền - góc nhọn)
Suy ra: \(DE = CF\) (\(2\) cạnh tương ứng).
dapandethi.vn
