Cho tam giác \(ABC\). Dựng về phía ngoài của tam giác các hình vuông \(BCIJ\), \(ACMN\), \(ABEF\)và gọi \(O\), \(P\), \(Q\) lần lượt là tâm đối xứng của chúng
LG a
Gọi \(D\) là trung điểm của \(AB\). Chứng minh rằng \(DOP\) là tam giác vuông cân đỉnh \(D\)
Phương pháp giải:
Sử dụng định nghĩa:
Cho \(O\) và góc lượng giác \(\alpha\). Phép biến hình biến \(O\) thành chính nó, biến mỗi điểm \(M\) khác \(O\) thành điểm \(M’\) sao cho \(OM’=OM\) và góc lượng giác \((OM;OM’)\) bằng \(\alpha\) được gọi là phép quay tâm \(O\) góc \(\alpha\).
Sử dụng tính chất phép quay biến một đoạn thẳng thành đoạn thẳng bằng đoạn thẳng đã cho.
Lời giải chi tiết:
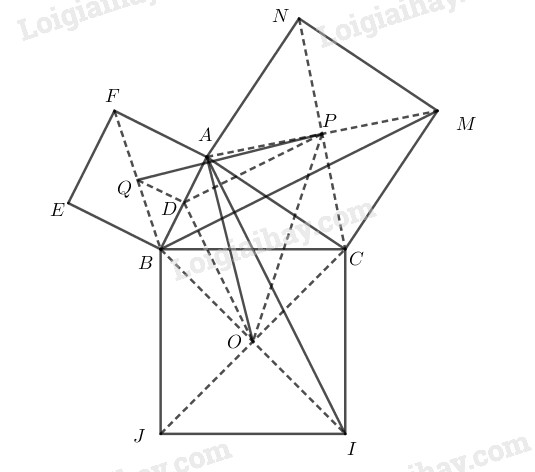
\(\begin{array}{l}
{Q_{\left( {C;{{90}^0}} \right)}}\left( M \right) = A\\
{Q_{\left( {C;{{90}^0}} \right)}}\left( B \right) = I
\end{array}\)
Do đó phép quay tâm \(C\) góc \({90}^o\) biến \(MB\) thành \(AI\).
Nên \(MB\) bằng và vuông góc với \(AI\).
Tam giác ABM có DP là đường trung bình nên \(DP\)//\(BM\) và \(DP = \frac{1}{2}BM\).
Tam giác ABI có DO là đường trung bình nên \(DO\)//\(AI\) và \(DO = \frac{1}{2}AI\)
Từ đó suy ra \(DP \bot DO\) và DP=DO.
Vậy tam giác \(DPO\) vuông tại \(D\).
LG b
Chứng minh \(AO\) vuông góc với \(PQ\) và \(AO=PQ\)
Phương pháp giải:
Sử dụng định nghĩa:
Cho \(O\) và góc lượng giác \(\alpha\). Phép biến hình biến \(O\) thành chính nó, biến mỗi điểm \(M\) khác \(O\) thành điểm \(M’\) sao cho \(OM’=OM\) và góc lượng giác \((OM;OM’)\) bằng \(\alpha\) được gọi là phép quay tâm \(O\) góc \(\alpha\).
Sử dụng tính chất phép quay biến một đoạn thẳng thành đoạn thẳng bằng độ dài đoạn thẳng đã cho.
Lời giải chi tiết:
Ta có:
\\(\begin{array}{l}
{Q_{\left( {D;{{90}^0}} \right)}}\left( A \right) = Q\\
{Q_{\left( {D;{{90}^0}} \right)}}\left( O \right) = P
\end{array}\)
Do đó phép quay tâm D góc quay \(90^0\) biến AO thành QP.
Do đó \(OA\) bằng và vuông góc với \(PQ\).
dapandethi.vn
