Tìm cực trị của các hàm số sau:
LG a
\(y = \sin^2 {x} - \sqrt 3 {\rm{cos}}x;x \in \left[ {0;\pi } \right]\)
Lời giải chi tiết:
\(y' = 2\sin x\cos x + \sqrt 3 \sin x\)
\( = \sin x(2\cos x + \sqrt 3 )\)
Với \(0 < x < \pi \) ta có \(\sin x > 0\). Do đó
\(y' = 0 \) \(\Leftrightarrow \cos x = - {{\sqrt 3 } \over 2} \Leftrightarrow x = {{5\pi } \over 6}\)
Bảng biến thiên
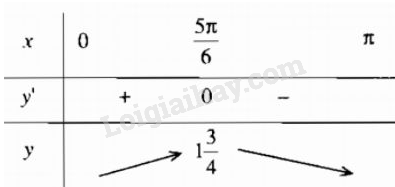
Hàm số đạt cực đại tại điểm \(x = {{5\pi } \over 6};y = \left( {{{5\pi } \over 6}} \right) = 1{3 \over 4}\)
Có thể áp dụng quy tắc 2
\(y' = \sin 2x + \sqrt 3 \sin x\)
\(y'' = 2\cos x + \sqrt 3 \cos x\)
\(y'' = \left( {{{5\pi } \over 6}} \right) = 2\cos {{5\pi } \over 6} + \sqrt 3 \cos {{5\pi } \over 6} \)
\(= 2.{1 \over 2} + \sqrt 3 \left( { - {{\sqrt 3 } \over 2}} \right) = - {1 \over 2} < 0\)
Vậy hàm số đạt cực đại tại điểm \(x = {{5\pi } \over 6};y = \left( {{{5\pi } \over 6}} \right) = 1{3 \over 4}\)
LG b
\(y = 2\sin x + {\rm{cos2}}x;x \in \left[ {0;\pi } \right]\)
Lời giải chi tiết:
\(y' = 2\cos x - 2\sin 2x\) \(= 2\cos x(1 - 2\sin x)\)
Với \(0 < x < \pi \) , ta có
\(y' = 0 \)\(\Leftrightarrow \left[ \matrix{ \cos x = 0 \hfill \cr \sin x = {1 \over 2} \hfill \cr} \right.\)\(\Leftrightarrow x = {\pi \over 2},x = {\pi \over 6},x = {{5\pi } \over 6}\)
Ta áp dụng quy tắc 2
\(y'' = - 2\sin x - 4\cos 2x\)
\(y'' = \left( {{\pi \over 2}} \right) = - 2\sin {\pi \over 2} - 4\cos x = 2 > 0\)
Hàm số đạt cực tiểu tại điểm \(x = {\pi \over 2};y\left( {{\pi \over 2}} \right) = 1\)
\(y''\left( {{\pi \over 6}} \right) = - 2\sin {\pi \over 6} - 4\cos {\pi \over 3} = - 3 < 0\)
Hàm số đạt cực đại tại điểm \(x = {\pi \over 6};y\left( {{\pi \over 6}} \right) = {3 \over 2}\)
\(y'' = \left( {{{5\pi } \over 6}} \right) = - 2\sin {{5\pi } \over 6} - 4\cos x{{5\pi } \over 3} = - 3 < 0\)
Hàm số đạt cực đại tại điểm \(x = {{5\pi } \over 6};\)\(y = \left( {{{5\pi } \over 6}} \right) = {3 \over 2}\)
dapandethi.vn
