Đề bài
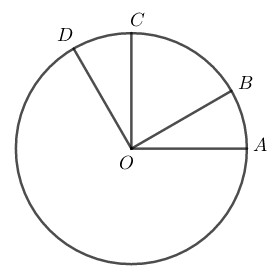
Cho hình \(bs.4.\) Biết \(\widehat{DOA}=120^o,\) \(OA\) vuông góc với \(OC,\) \(OB\) vuông góc với \(OD.\)
\(a)\) Đọc tên các góc ở tâm có số đo nhỏ hơn \(180^o.\)
\(b)\) Cho biết số đo của mỗi góc ở tâm tìm được ở câu trên.
\(c)\) Cho biết tên của các cặp cung có số đo bằng nhau (nhỏ hơn \(180^o\)).
\(d)\) So sánh hai cung nhỏ \(AB\) và \(BC.\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
+) Cung nhỏ có số đo nhỏ hơn \(180^o.\)
+) Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.
Lời giải chi tiết
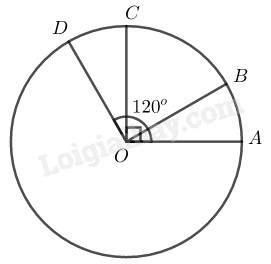
\(a)\) Các góc ở tâm có số đo nhỏ hơn \(180^o\) là:
\(\widehat {AOB},\widehat {AOC},\widehat {AOD},\widehat {BOC},\widehat {BOD},\widehat {COD}\)
\(b)\) \(OA \bot OC \Rightarrow \widehat {AOC} = {90^0}\)
\(OB \bot OD \Rightarrow \widehat {BOD} = {90^0}\)
\(\widehat {AOB} + \widehat {BOD} = \widehat {AOD}\)
\( \Rightarrow \widehat {AOB} = \widehat {AOD} - \widehat {BOD} \)\(= {120^0} - {90^0} = {30^0}\)
\(\widehat {AOC} + \widehat {COD} = \widehat {AOD}\)
\( \Rightarrow \widehat {COD} = \widehat {AOD} - \widehat {AOC} \)\(= {120^0} - {90^0} = {30^0}\)
\(\widehat {AOB} + \widehat {BOC} = \widehat {AOC}\)
\( \Rightarrow \widehat {BOC} = \widehat {AOC} - \widehat {AOB} \)\(= {90^0} - {30^0} = {60^0}\)
\(c)\) Các cung có số đo bằng nhau nhỏ hơn \(180^o\) là:
\(\overparen{AB} = \overparen{CD};\) \(\overparen{AC} = \overparen{BD}\)
\(d)\) \( sđ \overparen{AB}= \widehat {AOB} = {30^0}\)
\(sđ \overparen{BC}\)\( = \widehat {BOC} = {60^0}\)
Suy ra: \(sđ \overparen{BC}\) gấp đôi \(sđ \overparen{AB}\)
dapandethi.vn
