Đề bài
Cho tam giác \(ABC\) có \(AB > AC.\) Trên cạnh \(AB\) lấy một điểm \(D\) sao cho \(AD = AC.\) Vẽ đường tròn tâm \(O\) ngoại tiếp tam giác \(DBC.\) Từ \(O\) lần lượt hạ các đường thẳng vuông góc \(OH,\) \(OK\) xuống \(BC\) và \(BD\) (\(H \in BC,K \in BD\)).
\(a)\) Chứng minh rằng \(OH < OK.\)
\(b)\) So sánh hai cung nhỏ \(BD\) và \(BC.\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Trong một tam giác, độ dài một cạnh lớn hơn hiệu độ dài hai cạnh còn lại.
+) Trong một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn.
+) Với hai cung nhỏ trong một đường tròn, dây lớn hơn căng cung lớn hơn.
Lời giải chi tiết
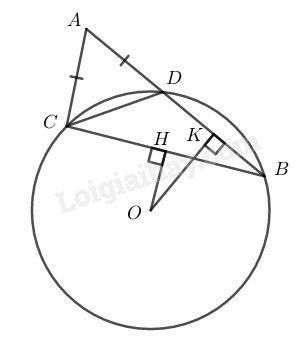
\(a)\) Trong \(∆ABC\) ta có:
\(BC > AB – AC\) (bất đẳng thức tam giác)
Mà \(AC = AD \;\; (gt)\)
\( \Rightarrow BC > AB – AD\)
Hay \(BC > BD\)
Trong \((O)\) ta có: \(BC > BD\)
\( \Rightarrow OH < OK\) (dây lớn hơn gần tâm hơn)
\(b)\) Ta có dây cung \(BC > BD\)
Suy ra: \(\overparen{BC}\) > \(\overparen{BD}\) (dây lớn hơn căng cung lớn hơn).
dapandethi.vn
