Đề bài
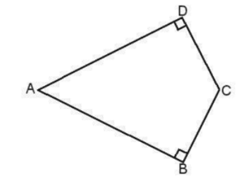
Tính chu vi và diện tích của hình bên, biết AB = AD = 4 cm, BC = CD = 2 cm, các góc B và D đều là góc vuông.
Phương pháp giải - Xem chi tiết
Bước 1: Tính chu vi bằng tổng độ dài các cạnh.
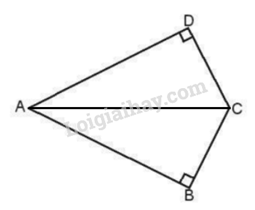
Bước 2: Để tính diện tích, ta chia hình đó thành 2 tam giác vuông (ABC và ADC)
Lời giải chi tiết
+) Chu vi của hình là:
P = AB + BC + CD + DA = 4 + 2 + 2 + 4 = 12 (cm)
+) Chia hình đã cho thành 2 hình tam giác ABC và ADC, lần lượt vuông tại B và D.
Ta có: tổng diện tích hai tam giác bằng diện tích hình đã cho.
Mà diện tích tam giác ABC là:
\({S_1} = \frac{1}{2}.AB.BC = \frac{1}{2}.4.2 = 4(c{m^2})\)
Và diện tích tam giác ADC là: \({S_2} = \frac{1}{2}.AD.DC = \frac{1}{2}.4.2 = 4(c{m^2})\)
Do đó diện tích hình đã cho là: \(S = {S_1} + {S_2} = 4 + 4 = 8(c{m^2})\)