Chọn đáp án đúng:
Bài 1
Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất :
(A) Hai mặt
(B) Ba mặt
(C) Bốn mặt
(D) Năm mặt.
Lời giải chi tiết:
Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất ba mặt.
Chọn B.
Bài 2
Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và D. Bằng hai mặt phẳng (MCD) và (NAB) ta chia khối tứ diện đã cho thành bốn khối tứ diện :
(A) AMCN,AMND,AMCD,BMCN;
(B) AMCN,AMND,BMCN,BMND;
(C) AMCD,AMND,BMCN,BMND;
(D) BMCD,BMND,AMCN,AMDN.
Lời giải chi tiết:
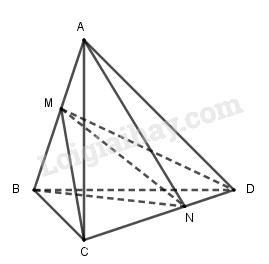
Các khối tứ diện được tạo thành là: AMCN,AMND,BMCN,BMND.
Chọn B.
Bài 3
Phép đối xứng qua mặt phẳng \(\left( P \right)\) biến đường thẳng d thành đường thẳng d’ cắt d khi và chỉ khi :
(A) d cắt \(\left( P \right)\);
(B) d nằm trên \(\left( P \right)\);
(C) d cắt \(\left( P \right)\) nhưng không vuông góc với \(\left( P \right)\);
(D) d không vuông góc với \(\left( P \right)\).
Lời giải chi tiết:
Phép đối xứng qua mặt phẳng \(\left( P \right)\) biến đường thẳng d thành đường thẳng d’ cắt d khi và chỉ khi d cắt \(\left( P \right)\) nhưng không vuông góc với \(\left( P \right)\).
Chọn C.
Bài 4
Số mặt phẳng đối xứng của hình lập phương là
(A) 6
(B) 7
(C) 8
(D) 9
Lời giải chi tiết:
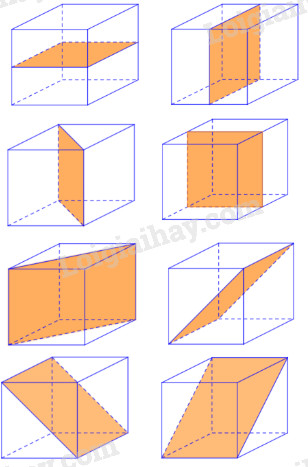
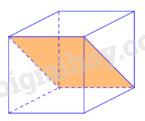
Hình lập phương có 9 mặt phẳng đối xứng.
Chọn D.
Bài 5
Số mặt phẳng đối xứng của bát diện đều là :
(A) 3
(B) 6
(C ) 9
(D) 12
Lời giải chi tiết:
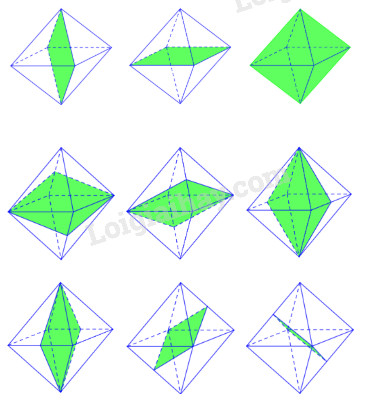
Số mặt phẳng đối xứng của bát diện đều là 9.
Chọn C.
Bài 6
Số mặt phẳng đối xứng của hình tứ diện đều là :
(A) 4
(B) 6
(C ) 8
(D) 10
Lời giải chi tiết:
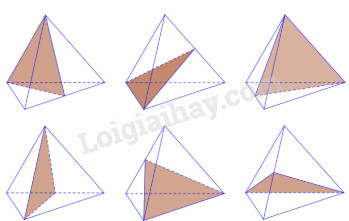
Số mặt phẳng đối xứng của hình tứ diện đều là 6.
Chọn B.
Bài 7
Hình H gồm ba mặt phẳng (P), (Q),và (R),trong đó \(\left( P \right)//\left( Q \right)\) và \(\left( P \right) \bot \left( R \right)\). Các mặt phẳng đối xứng của H là
(A) Mặt phẳng cách đều hai mặt phẳng (P) và (Q);
(B) Mặt phẳng (R ) và mặt phẳng cách đều (P) và (Q);
(C ) Mặt phẳng (R );
(D) Cả ba đáp án đều sai.
Lời giải chi tiết:
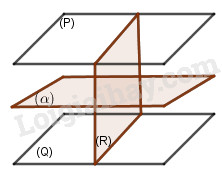
Các mặt phẳng đối xứng của H là: Mặt phẳng (R) và mặt phẳng cách đều (P) và (Q).
Chọn B.
Bài 8
Thực hiện liên tiếp phép vị tự tâm O tỉ số k và phép đối xứng qua mặt phẳng \(\left( P \right)\),\(\left( {O \notin \left( P \right)} \right)\), ta được phép biến hình f. Giả sử (Q) là mặt phẳng qua O và vuông góc với (P). Khi đó f biến (Q) thành :
(A) Mặt phẳng (Q’) song song với (Q);
(B) Mặt phẳng (P) ;
(C) Mặt phẳng (Q) ;
(D) Mặt phẳng (P’) qua O và song song với (P).
Lời giải chi tiết:
Vì \(O \in \left( Q \right)\) nên \({V_{\left( {O;k} \right)}}\left( {\left( Q \right)} \right) = \left( Q \right)\).
\(\left( Q \right) \bot \left( P \right)\) nên \({D_{\left( {\left( P \right)} \right)}}\left( {\left( Q \right)} \right) = \left( Q \right)\)
Vậy f biến \(\left( Q \right)\) thành chính nó.
Bài 9
Trong các mệnh đề sau đây, mệnh đề nào đúng ?
(A) Phép vị tự biến mặt phẳng thành mặt phẳng song song với nó.
(B) Phép vị tự biến mặt phẳng qua tâm vị tự thành chính nó ;
(C ) Không có phép vị tự nào biến hai điểm phân biệt A và B lần lượt thành A và B ;
(D) Phép vị tự biến đường thẳng thành đường thẳng song song với nó.
Lời giải chi tiết:
Chọn B.
Bài 10
Khối mười hai mặt đều thuộc loại :
\(\eqalign{ & (A)\left\{ {3,5} \right\}; \cr & (B)\left\{ {3,6} \right\}; \cr & (C)\left\{ {5,3} \right\}; \cr & (D)\left\{ {4,4} \right\}. \cr} \)
Lời giải chi tiết:
Khối mười hai mặt đều thuộc loại {5,3}.
Chọn C.
Bài 11
Đáy của một hình hộp đứng là một hình thoi có đường chéo nhỏ bằng d và góc nhọn bằng \(\alpha \). Diện tích của một mặt bên bằng S. Thể tích của hình hộp đã cho là :
\(\eqalign{ & (A)\;dS\cos {\alpha \over 2}; \cr & (B)\;dS\sin {\alpha \over 2}; \cr & (C)\;{1 \over 2}dS\sin \alpha ; \cr & (D)\;dS\sin \alpha . \cr} \)
Lời giải chi tiết:
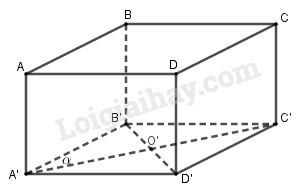
Xét hình hộp ABCD.A’B’C’D’ thỏa mãn bài toán.
ở đó, \(\widehat {B'A'D'} = \alpha ,B'D' = d\).
Gọi O’ là giao điểm của A’C’ và B’D’.
\(\begin{array}{l} \Rightarrow A'D' = \frac{{O'D'}}{{\sin \frac{\alpha }{2}}} = \frac{d}{{2\sin \frac{\alpha }{2}}}\\ \Rightarrow {S_{A'B'C'D'}} = A'D'.A'B'.\sin \alpha \\ = \frac{d}{{2\sin \frac{\alpha }{2}}}.\frac{d}{{2\sin \frac{\alpha }{2}}}.\sin \alpha = \frac{{{d^2}\cos \frac{\alpha }{2}}}{{2\sin \frac{\alpha }{2}}}\\DD' = \frac{{{S_{ADD'A'}}}}{{A'D'}} = \frac{S}{{\frac{d}{{2\sin \frac{\alpha }{2}}}}} = \frac{{2S\sin \frac{\alpha }{2}}}{d}\\ \Rightarrow {V_{ABCD.A'B'C'D'}} = {S_{A'B'C'D'}}.DD'\\ = \frac{{{d^2}\cos \frac{\alpha }{2}}}{{2\sin \frac{\alpha }{2}}}.\frac{{2S\sin \frac{\alpha }{2}}}{d} = dS\cos \frac{\alpha }{2}\end{array}\)
Bài 12
Cho khối lăng trụ tam giác ABC.A’B’C’ có thể tích là V. Gọi I và J lần lượt là trung điểm của hai cạnh AA’ và BB’. Khi đó thể tích của khối đa diện ABCIJC’ bằng
\(\eqalign{ & (A)\;{3 \over 4}V; \cr & (B)\;{4 \over 5}V; \cr & (C)\;{2 \over 3}V; \cr & (D)\;{3 \over 5}V. \cr} \)
Lời giải chi tiết:
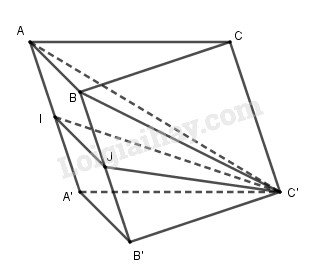
\(\begin{array}{l}
{V_{C'ABC}} = \frac{1}{3}V\\
\Rightarrow {V_{C'.ABB'A'}} = \frac{2}{3}V\\
\Rightarrow {V_{C'.A'B'JI}} = \frac{1}{2}{V_{C'.ABB'A'}}\\
= \frac{1}{2}.\frac{2}{3}V = \frac{1}{3}V\\
\Rightarrow {V_{ABCIJC'}} = V - \frac{1}{3}V = \frac{2}{3}V
\end{array}\)
Chọn C.
Bài 13
Cho hình hộp ABCD.A’B’C’D’ có đáy là một hình thoi và hai mặt chéo ACC’A’, BDD’B đều vuông góc với mặt phẳng đáy. Hai mặt này có diện tích lần lượt là 100cm2, 105cm2 và cắt nhau theo một đường thẳng có độ dài 10cm. Khi đó thể tích của hình hộp đã cho là
\(\eqalign{ & (A)\;225\sqrt 5 c{m^3}; \cr & (B)\;235\sqrt 5 c{m^3}; \cr & (C)\;425c{m^3}; \cr & (D)\;525c{m^3}. \cr} \)
Lời giải chi tiết:
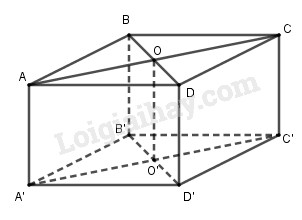
Gọi O, O’ lần lượt là tâm các hình thoi.
Khi đó \(\left( {ACC'A'} \right) \cap \left( {BDD'B'} \right) = OO'\)
Mà \(\left( {ACC'A'} \right)\) và \(\left( {BDD'B'} \right)\) cùng vuông góc với đáy nên:
\(OO' \bot \left( {A'B'C'D'} \right)\) và \(OO' = 10\left( {cm} \right)\)
\( \Rightarrow AA' = BB' = CC' = DD' = 10\left( {cm} \right)\)
\({S_{BDD'B'}} = 100\left( {c{m^2}} \right)\) \( \Rightarrow B'D' = \frac{{{S_{BDD'B'}}}}{{BB'}} = \frac{{100}}{{10}} = 10\left( {cm} \right)\)
\({S_{ACC'A'}} = 105\left( {c{m^2}} \right)\) \( \Rightarrow A'C' = \frac{{{S_{ACC'A'}}}}{{AA'}} = \frac{{105}}{{10}} = 10,5\left( {cm} \right)\)
Vậy thể tích:
\(\begin{array}{l}{V_{ABCD.A'B'C'D'}} = {S_{A'B'C'D'}}.AA'\\ = \frac{1}{2}A'C'.B'D'.AA'\\ = \frac{1}{2}.10,5.10.10 = 525\left( {c{m^3}} \right)\end{array}\)
Chọn D.
Bài 14
Khối lăng trụ ABC.A’B’C’ có đáy là một tam giác đều cạnh a, góc giữa cạnh bên và mặt phẳng đáy bằng 300. Hình chiếu của đỉnh A’ trên mặt phẳng đáy (ABC) trùng với trung điểm của cạnh BC. Thể tích của khối lăng trụ đã cho là
\(\eqalign{ & (A)\;{{{a^3}\sqrt 3 } \over 4}; \cr & (B)\;{{{a^3}\sqrt 3 } \over 8}; \cr & (C)\;{{{a^3}\sqrt 3 } \over 3}; \cr & (D)\;{{{a^3}\sqrt 3 } \over {12}}. \cr} \)
Lời giải chi tiết:
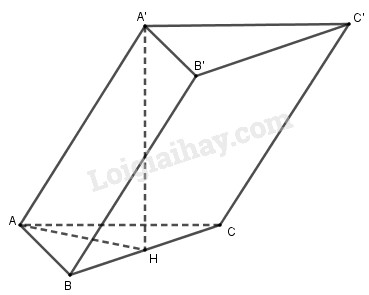
Gọi H là trung điểm của BC.
Khi đó \(AH \bot \left( {ABC} \right),AH = \frac{{a\sqrt 3 }}{2}\),\({S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\)
Do \(A'H \bot \left( {ABC} \right)\) nên góc giữa AA’ và (ABC) bằng góc \(\widehat {A'AH} = {30^0}\).
Tam giác A’AH vuông tại H nên \(A'H = AH\tan \widehat {A'AH}\) \( = \frac{{a\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{3} = \frac{a}{2}\).
Thể tích \({V_{ABC.A'B'C'}} = {S_{ABC}}.A'H\) \( = \frac{{{a^2}\sqrt 3 }}{4}.\frac{a}{2} = \frac{{{a^3}\sqrt 3 }}{8}\).
Chọn B.
Bài 15
Hình hộp chữ nhật ABCD.A’B’C’D’ có diện tích các mặt ABCD, ABB’A’, ADD’A’ lần lượt bằng 20cm2, 28 cm2 và 35cm2. Thể tích của hình hộp là
\(\eqalign{ & (A)\;160c{m^3}; \cr & (B)\;120c{m^3}; \cr & (C)\;130c{m^3}; \cr & (D)\;140c{m^3}. \cr} \)
Lời giải chi tiết:
\(\begin{array}{l}
{S_{ABCD}} = AB.AD = 20\\
{S_{ABB'A'}} = AB.AA' = 28\\
{S_{ADD'A'}} = AA'.AD = 35\\
\Rightarrow A{B^2}.A{D^2}.AA{'^2}\\
= 20.28.35 = 196000\\
\Rightarrow AB.AD.AA' = 140\\
\Rightarrow {V_{ABCD.A'B'C'D'}} = AB.AD.AA'\\
= 140\left( {c{m^3}} \right)
\end{array}\)
dapandethi.vn
