Câu 1
Viết số thích hợp vào ô trống:
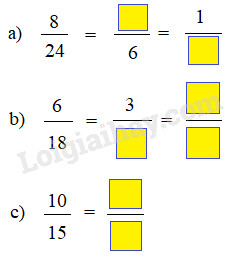
Phương pháp giải:
Khi rút gọn phân số ta có thể làm như sau :
• Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
• Chia cả tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Lời giải chi tiết:
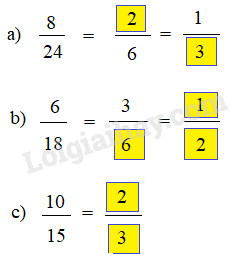
Câu 2
Trả lời câu hỏi:
Phân số nào trong các phân số : \(\dfrac{1}{5}\,\,;\,\,\dfrac{6}{7}\,;\,\,\dfrac{9}{{19}}\,;\,\,\dfrac{{16}}{{32}}\) là phân số tối giản ? Vì sao ?
Phương pháp giải:
Áp dụng định nghĩa : Phân số tối giản là phân số có tử số và mãu số không cùng chia hết cho một số tự nhiên nào lớn hơn 1, hay phân số tối giản là phân số không thể rút gọn được nữa.
Lời giải chi tiết:
Trong các phân số đã cho, phân số tối giản là : \(\dfrac{1}{5}\,\,;\,\,\dfrac{6}{7}\,;\,\,\dfrac{9}{{19}}\) vì những phân số này không thể rút gọn được nữa.
Câu 3
Rút gọn các phân số:
\(a)\,\,\dfrac{{15}}{{18}}\,\,;\) \(b)\,\,\dfrac{{30}}{{120}}\,\,;\) \(c)\,\,\dfrac{{45}}{{27}}\,\,;\) \(d)\,\,\dfrac{{75}}{{300}}.\)
Phương pháp giải:
Khi rút gọn phân số ta có thể làm như sau :
• Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
• Chia cả tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Lời giải chi tiết:
\(a)\,\,\dfrac{{15}}{{18}} = \dfrac{{15:3}}{{18:3}} = \dfrac{5}{6}\,\,;\) \(b)\,\,\dfrac{{30}}{{120}} = \dfrac{{30:30}}{{120:30}} = \dfrac{1}{4}\,\,;\)
\(c)\,\,\dfrac{{45}}{{27}}\, = \dfrac{{45:9}}{{27:9}} = \dfrac{5}{3}\,;\) \(d)\,\,\dfrac{{75}}{{300}} = \dfrac{{75:75}}{{300:75}} = \dfrac{1}{4}.\)
Câu 4
Tính rồi viết (theo mẫu):
Mẫu :
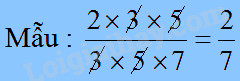
Chú ý : Trong mẫu trên, ta đã cùng chia nhẩm tích ở trên và tích ở dưới gạch ngang cho 3, sau đó tiếp tục cùng chia nhẩm cho 5.
\(a)\,\,\dfrac{{4 \times 2 \times 9}}{{7 \times 9 \times 4}}\,\,;\) \(b)\,\,\dfrac{{5 \times 8 \times 17}}{{8 \times 3 \times 5}}.\)

Phương pháp giải:
Cùng chia nhẩm tích ở tử số và mẫu số cho các thừa số chung.
Lời giải chi tiết:
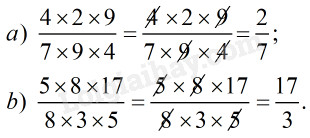
dapandethi.vn
