Câu 1
Chơi trò chơi “Ai nhanh, ai thông minh hơn ?” :
- Em viết rổi đọc một phân số bất kì, chẳng hạn : \(\dfrac{2}{3}\).
- Các bạn trong nhóm tìm các phân số bằng phân số em đã viết.
- Cử đại diện ghi lại các phân số nhóm mình viết được. Nhóm nào viết được nhiều phân số nhất sẽ thắng cuộc.

Phương pháp giải:
- Khi viết phân số ta viết tử số trên gạch ngang, viết mẫu số dưới gạch ngang.
- Khi đọc phân số ta đọc tử số trước, dấu gạch ngang đọc là “phần”, sau đó đọc mẫu số.
- Để tìm các phân số bằng phân số \(\dfrac{2}{3}\) ta có thể nhân cả tử số và mẫu số của phân số \(\dfrac{2}{3}\) với các số tự nhiên \(2;3;4;....\) .
Lời giải chi tiết:
Ví dụ :
- Em viết phân số \(\dfrac{3}{4}\), đọc là “ba phần tư”.
- Các phân số bằng với phân số là \(\dfrac{3}{4}\): \(\dfrac{6}{8}\,\,;\,\,\,\dfrac{9}{{12}}\,\,;\,\,\,\dfrac{{12}}{{16}}\,\,;\,\,\,\dfrac{{15}}{{20}}\,\,;\,\,\,\dfrac{{18}}{{24}}\,\,;\,\,\,\dfrac{{21}}{{28}}\) \(\,\,;\,\,\,\dfrac{{24}}{{32}}\,\,;\,\,\,\dfrac{{27}}{{36}}\,\,;\,\,\,\dfrac{{30}}{{40}}\,\,;\,\,\,\dfrac{{33}}{{44}}\,\,;\,\,...\)
Câu 2
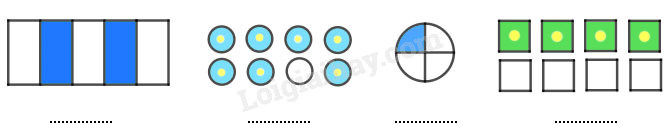
a) Viết phân số chỉ phần đã tô màu trong mỗi hình dưới đây:
b) Rút gọn phân số: \(\dfrac{4}{6};\dfrac{9}{{12}};\dfrac{{10}}{{20}};\dfrac{8}{{18}}\)
Phương pháp giải:
a) - Quan sát kĩ các hình vẽ để viết phân số tương ứng với mỗi hình.
- Trong mỗi phân số, tử số chỉ số phần bằng nhau đã được tô màu và mẫu số chỉ tổng số phần bằng nhau.
b) Khi rút gọn phân số ta có thể làm như sau :
• Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
• Chia cả tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
Lời giải chi tiết:
a)
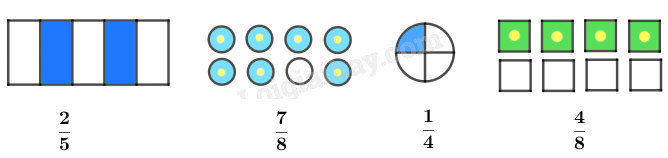
b)
\(\begin{array}{*{20}{l}}
{\dfrac{4}{6} = \dfrac{{4:2}}{{6:2}} = \dfrac{2}{3}}\\
{\dfrac{9}{{12}} = \dfrac{{9:3}}{{12:3}} = \dfrac{3}{4}}\\
{\dfrac{{10}}{{20}} = \dfrac{{10:10}}{{20:10}} = \dfrac{1}{2}}\\
{\dfrac{8}{{18}} = \dfrac{{8:2}}{{18:2}} = \dfrac{4}{9}}
\end{array}\)
Câu 3
So sánh hai phân số:
a) \(\dfrac{1}{3}\) và \(\dfrac{1}{4}\) ; \(\dfrac{3}{5}\) và \(\dfrac{5}{6}\).
b) \(\dfrac{3}{{10}}\) và \(\dfrac{8}{5}\) ; \(\dfrac{4}{3}\) và \(\dfrac{7}{6}\).
c) \(\dfrac{7}{4}\) và \(\dfrac{1}{6}\) ; \(\dfrac{5}{6}\) và \(\dfrac{7}{8}\).
Phương pháp giải:
Áp dụng các quy tắc so sánh phân số :
- Trong hai phân số có cùng mẫu số, phân số nào có tử số bé hơn thì phân số đó bé hơn hơn.
- Trong hai phân số có cùng tử số, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.
- Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới.
Lời giải chi tiết:
a) • \(\dfrac{1}{3}\) và \(\dfrac{1}{4}\)
\(\dfrac{1}{3} > \dfrac{1}{4}\) (vì \(3 < 4\)).
• \(\dfrac{3}{5}\) và \(\dfrac{5}{6}\)
\(\begin{array}{*{20}{l}}
{\dfrac{3}{5} = \dfrac{{3 \times 6}}{{5 \times 6}} = \dfrac{{18}}{{30}}}\\
{\dfrac{5}{6} = \dfrac{{5 \times 5}}{{6 \times 5}} = \dfrac{{25}}{{30}}}
\end{array}\)
Mà \(\dfrac{{18}}{{30}} < \dfrac{{25}}{{30}}\) (vì \(18 < 25\))
Vậy \(\dfrac{3}{5} < \dfrac{5}{6}\).
b) • \(\dfrac{3}{{10}}\) và \(\dfrac{8}{5}\)
Cách 1 :
Giữ nguyên phân số \(\dfrac{3}{{10}}\) ;
\(\dfrac{8}{5} = \dfrac{{8 \times 2}}{{5 \times 2}} = \dfrac{{16}}{{10}}\)
Mà \(\dfrac{3}{10} < \dfrac{16}{10}\) (vì \(3 < 16\)).
Vậy \(\dfrac{3}{{10}} < \dfrac{8}{5}\).
Cách 2 :
Ta có : \(\dfrac{3}{{10}} < 1\) và \(\dfrac{8}{5} > 1\).
Hay \(\dfrac{3}{{10}} < 1< \dfrac{8}{5}\).
Vậy \(\dfrac{3}{{10}} < \dfrac{8}{5}\).
• \(\dfrac{4}{3}\) và \(\dfrac{7}{6}\)
\( \dfrac{4}{3} = \dfrac{{4 \times 2}}{{3 \times 2}} = \dfrac{8}{6}\)
Giữ nguyên phân số \(\dfrac{7}{6} \)
Mà \(\dfrac{8}{6} > \dfrac{7}{6}\) (vì \(8 > 7\)).
Vậy \(\dfrac{4}{3} > \dfrac{7}{6}\).
c) • \(\dfrac{7}{4}\) và \(\dfrac{1}{6}\)
Cách 1 :
\(\begin{array}{*{20}{l}}
{\dfrac{7}{4} = \dfrac{{7 \times 3}}{{4 \times 3}} = \dfrac{{21}}{{12}}}\\
{\dfrac{1}{6} = \dfrac{{1 \times 2}}{{6 \times 2}} = \dfrac{2}{{12}}}
\end{array}\)
Mà \(\dfrac{21}{12} > \dfrac{2}{12}\) (vì \(21 > 2\)).
Vậy \(\dfrac{7}{4} > \dfrac{1}{6}\).
Cách 2 :
Ta có : \(\dfrac{7}{4} > 1 \;; \;\; \dfrac{1}{6} < 1\).
Hay \(\dfrac{7}{4} >1 > \dfrac{1}{6}\).
Vậy \(\dfrac{7}{4} > \dfrac{1}{6}\).
• \(\dfrac{5}{6}\) và \(\dfrac{7}{8}\)
\(\begin{array}{*{20}{l}}
{\dfrac{5}{6} = \dfrac{{5 \times 4}}{{6 \times 4}} = \dfrac{{20}}{{24}}}\\
{\dfrac{7}{8} = \dfrac{{7 \times 3}}{{8 \times 3}} = \dfrac{{21}}{{24}}}
\end{array}\)
Mà \(\dfrac{20}{24} < \dfrac{21}{24}\) (vì \(20 < 21\)).
Vậy \(\dfrac{5}{6} < \dfrac{7}{8}\).
Câu 4
Đặt tính rồi tính:
a) 780139 + 23507 ; 364563 – 91904 ;
b) 512 × 307 ; 70308 : 217.
Phương pháp giải:
- Với phép tính cộng, trừ, nhân : Đặt tính sao cho các chữ số ở cùng hàng thì thẳng cột với nhau, sau đó thực hiện phép tính theo thứ tự từ phải sang trái.
- Với phép chia : Đặt tính theo cột dọc, sau đó chia theo thứ tự từ trái sang phải.
Lời giải chi tiết:

Câu 5
Viết chữ số thích hợp vào ô trống sao cho :
a) \(67\square \) chia hết cho 5 nhưng không chia hết cho 2.
b) \(67\square \) chia hết cho 9.
Phương pháp giải:
Áp dụng các dấu hiệu chia hết cho 2; 5; 9; 3:
- Các số có chữ số tận cùng là 0; 2; 4; 6; 8 thì chia hết cho 2.
- Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5.
- Các số có chữ số tận cùng là 0 thì chia hết cho cả 2 và 5.
- Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9.
Lời giải chi tiết:
a) Giả sử chữ số cần điền vào ô trống là \(x\).
Vì số \(\overline {67x} \) chia hết cho 5 nhưng không chia hết cho 2 nên chữ số tận cùng phải là 5, hay \(x \) = 5.
Vậy số cần tìm là: 675.
b) Giả sử chữ số cần điền vào ô trống là \(x\).
Vì số \(\overline {67x} \) chia hết cho 9 nên \(6 + 7 + x\) chia hết cho 9, hay \(13+x\) chia hết cho 9.
Suy ra \(x\) = 5.
Vậy số cần tìm là: 675.
dapandethi.vn
