Câu hỏi 1 :
Một mạch điện xoay chiều gồm R, L, C nối tiếp nhau. Nếu hiệu điện thế giữa hai đầu đoạn mạch là $u = {U_0}{\text{cos}}\left( {\omega t - \frac{\pi }{6}} \right)$ thì cường độ dòng điện trong mạch là $i = {I_0}\sin \left( {\omega t + \frac{\pi }{3}} \right)$. Thì dòng điện có:
- A $\omega = \frac{1}{{\sqrt {LC} }}$
- B \(omega < \frac{1}{{LC}}\)
- C $\omega > \frac{1}{{\sqrt {LC} }}$
- D $\omega < \frac{1}{{\sqrt {LC} }}$
Đáp án: D
Phương pháp giải:
Phương pháp:
+ Xác định độ lệch pha giữa u và i: $\varphi = {\varphi _u} - {\varphi _i}$
+ So sánh ZL và ZC
Lời giải chi tiết:
Đáp án D
Cách giải:
Ta có: u trễ pha hơn i một góc p/2
=> Mạch có \({Z_L} < {Z_C}\; \leftrightarrow L\omega < \frac{1}{{C\omega }} \to {\omega ^2} < \frac{1}{{LC}} \to \omega < \frac{1}{{\sqrt {LC} }}\)
=> Chọn D
Câu hỏi 2 :
Cho một đoạn mạch xoay chiều nối tiếp gồm điện trở R, cuộn cảm thuần cảm L và tụ C. Đặt vào hai đầu đoạn mạch hiệu điện thế \(u = 100\sqrt 2 {\text{cos}}\omega {\text{t}}\left( V \right)\), lúc đó ZL = 2ZC và hiệu điện thế hiệu dụng hai đầu điện trở là UR = 60V. Hiệu điện thế hiệu dụng hai đầu cuộn dây là:
- A 60V
- B 80V
- C 120V
- D 160V
Đáp án: D
Phương pháp giải:
Phương pháp: Sử dụng công thức: \({U^2} = U_R^2 + {\left( {{U_L} - {U_C}} \right)^2}\)
Lời giải chi tiết:
Đáp án D
Cách giải:
Ta có: ZL = 2ZC => UL = 2UC
\(\eqalign{
& {U^2} = U_R^2 + {\left( {{U_L} - {U_C}} \right)^2} = U_R^2 + {\left( {{U_L} - {{{U_L}} \over 2}} \right)^2} = U_R^2 + {{{{U_L}} \over 4}^2} \cr
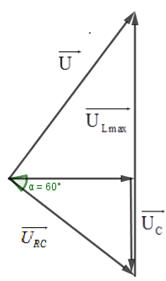
& \to {U_L} = 2\sqrt {{U^2} - U_R^2} = 2\sqrt {{{100}^2} - {{60}^2}} = 160V \cr} \)
=> Chọn D
Câu hỏi 3 :
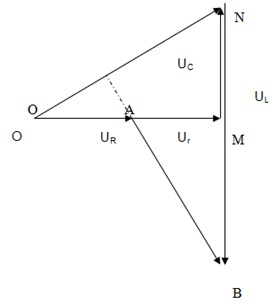
Trên một đoạn mạch xoay chiều không phân nhánh có 4 điểm theo thứ tự A, M, N , B. Giữa A và M chỉ có cuộn cảm thuần, giữa M và N chỉ có điện trở thuần, giữa N và B chỉ có tụ điện. Điện áp hiệu dụng UAN = 400V, UMB = 300V. Điện áp tức thời trên đoạn AN và MB lệch nhau 900. Điện áp hiệu dụng trên R là
- A 500V
- B 120V
- C 240V
- D 180V
Đáp án: C
Phương pháp giải:
Phương pháp: Sử dụng công thức: \({\varphi _1} + {\varphi _2} = \frac{\pi }{2} \to \left| {\tan {\varphi _1}\tan {\varphi _2}} \right| = 1\)
Lời giải chi tiết:
Đáp án C
Cách giải:
Ta có: \({U_{RL}} \bot {U_{RC}} \to \left| {\tan {\varphi _1}\tan {\varphi _2}} \right| = 1 \to \frac{{{Z_L}}}{R}\frac{{{Z_C}}}{R} = 1 \to {U_L}{U_C} = U_R^2\)
\(\eqalign{
& \left\{ \matrix{
U_R^2 + U_L^2 = {400^2}(1) \hfill \cr
U_R^2 + U_C^2 = {300^2}(2) \hfill \cr} \right. \cr
& (1) + (2) \leftrightarrow 2U_R^2 + U_L^2 + U_C^2 = {400^2} + {300^2} \leftrightarrow 2U_R^2 + {\left( {{U_L} + {U_C}} \right)^2} - 2{U_L}{U_C} = {400^2} + {300^2} \cr
& \to \left( {{U_L} + {U_C}} \right) = 500 \cr
& (1) - (2) \leftrightarrow U_L^2 - U_C^2 = {400^2} - {300^2} \leftrightarrow \left( {{U_L} + {U_C}} \right)\left( {{U_L} - {U_C}} \right) = {400^2} - {300^2} \to \left( {{U_L} - {U_C}} \right) = 140 \cr
& \to \left\{ \matrix{
{U_L} = 320 \hfill \cr
{U_C} = 140 \hfill \cr} \right. \to {U_R} = \sqrt {{{400}^2} - {{320}^2}} = 240V \cr} \)
=> Chọn C
Câu hỏi 4 :
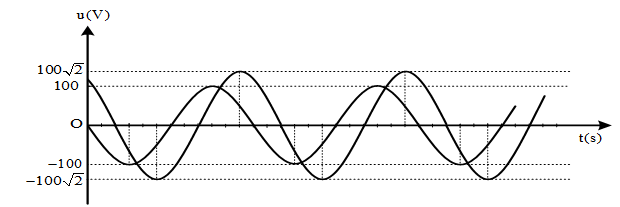
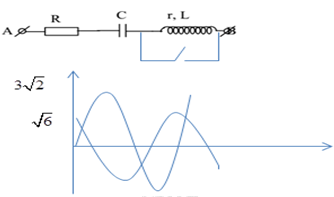
Đặt điện áp xoay chiều AB gồm: đoạn mạch AM chứa điện trở thuần R = 90Ω và tụ điện C = 35,4µF, đoạn mạch MB gồm hộp X chứa 2 trong 3 phần tử mắc nối tiếp (điện trở thuần R0; cuộn cảm thuần có độ tự cảm L0; tụ điện có điện dung C0). Khi đặt vào hai đầu AB một điện thế xoay chiều có tần số 50Hz thì ta được đồ thị sự phụ thuộc của uAM và uMB theo thời gian như hình vẽ (chú ý \(90\sqrt 3 \approx 156\)). Giá trị của các phần tử trong hộp X là
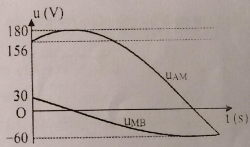
- A R0 = 60Ω; L0 = 165Mh
- B R0 = 30Ω; L0 = 95,5mH
- C R0 = 60Ω; L0 = 61,3mH
- D R0 = 30Ω; L0 = 106mH
Đáp án: B
Phương pháp giải:
Phương pháp: Sử dụng các công thức của dòng điện xoay chiều kết hợp kĩ năng đọc đồ thị
Lời giải chi tiết:
Đáp án B
Cách giải:
Ta có: R = 90W, ZC = 90W
Từ đồ thị, ta có: ${U_{{0_{AM}}}} = 180V;{U_{{0_{MB}}}} = 60V$
Tại thời điểm t = 0, ta có:
uAM = 156 và đang tăng $ \to {u_{AM}} = 156 = 180c{\text{os}}{\varphi _1} \to {\varphi _1} = - {30^0}$
uMB = 30 và đang giảm $ \to {u_{AM}} = 30 = 60c{\text{os}}{\varphi _2} \to {\varphi _2} = {60^0}$
$ \to {\varphi _2} - {\varphi _1} = {90^0} \to {u_{AM}} \bot {u_{MB}}$
=> hộp X gồm 2 phần tử R0 và L0
${u_{AM}} \bot {u_{MB}} \to \left| {\tan {\varphi _1}\tan {\varphi _2}} \right| = 1 \leftrightarrow \frac{{{Z_{{L_0}}}}}{{{R_0}}}\frac{{{Z_C}}}{R} = 1 \leftrightarrow \frac{{{Z_{{L_0}}}}}{{{R_0}}}\frac{{90}}{{90}} = 1 \to {Z_{{L_0}}} = {R_0}$
Mặt khác, ta có:
$\eqalign{
& {{{U_{{0_{AM}}}}} \over {{U_{{0_{MB}}}}}} = {{{Z_{AM}}} \over {{Z_{MB}}}} = {{180} \over {60}} = 3 \to {Z_{AM}} = 3{Z_{MB}} \leftrightarrow \sqrt {R_0^2 + Z_{{L_0}}^2} = 3.\sqrt {{{90}^2} + {{90}^2}} \cr
& \to {R_0} = {Z_{{L_0}}} = 30\Omega \to \left\{ \matrix{
{R_0} = 30\Omega \hfill \cr
{L_0} = 95,9mH \hfill \cr} \right. \cr} $
=> Chọn B
Câu hỏi 5 :
Nếu nối hai đầu đoạn mạch gồm cuộn cảm thuần L mắc nối tiếp với điện trở thuần R = 2,5Ω vào hai cực của nguồn điện một chiều có suất điện động không đổi và điện trở trong r thì trong mạch có dòng điện không đổi cường độ I1. Dùng nguồn điện này để nạp điện cho một tụ điện có điện dung C = 2.10-6F. Khi điện tích trên tụ điện đạt giá trị cực đại, ngắt tụ điện khỏi nguồn rồi nối tụ điện với cuộn cảm thuần L thành một mạch dạo động thì trong mạch có dao động điện từ tự do với chu kì bằng π.10-6 s và cường độ dòng điện cực đại bằng I2 = 12I1. Giá trị của r bằng
- A 0,25 Ω
- B 1,5 Ω
- C 0,5 Ω
- D 2 Ω
Đáp án: C
Lời giải chi tiết:
Đáp án C
\({I_1} = {\varepsilon \over {2,5 + r}}(1)\);\({1 \over 2}LI_2^2 = {1 \over 2}C{\varepsilon ^2} = > {I_2} = \varepsilon \sqrt {{C \over L}} \) ; ta có \(T = 2\pi \sqrt {LC} = > L = {{{T^2}} \over {4{\pi ^2}C}}\)=>\({I_2} = {{2\pi \varepsilon C} \over T}\)(2)
I2=12I1 =>\({{2\pi \varepsilon C} \over T} = 12.{\varepsilon \over {2,5 + r}}\); thay số =>r=0,5Ω
Câu hỏi 6 :
Mạch điện AB gồm đoạn AM và đoạn MB: Đoạn AM có một điện trở thuần 50Ω và đoạn MB có một cuộn dây. Đặt vào mạch AB một điện áp xoay chiều thì điện áp tức thời của hai đoạn AM và MB biến thiên như trên đồ thị:
Cảm kháng của cuộn dây là:
- A \(12,5\sqrt 2 \Omega \)
- B \(12,5\sqrt 3 \Omega \)
- C \(12,5\sqrt 6 \Omega \)
- D \(25\sqrt 6 \Omega \)
Đáp án: C
Lời giải chi tiết:
Đáp án C
Đoạn MB là cuộn dây, đoạn AM chỉ có điện trở nên uMB sớm pha hơn uAM; một chu kỳ ứng với 12 khoảng, nên ta thấy uMB sớm pha hơn uAM một góc \({\pi \over 3}\); uAM cùng pha với cường độ dòng điện nên uMB sớm pha hơn cường độ dòng điện một góc \({\pi \over 3}\); \(I={{{U_R}} \over R} = {{100\sqrt 2 } \over {\sqrt {2.} 50}} = 2(A)\)=>\({Z_{MB}} = {{{U_{MB}}} \over I} = {{100} \over {\sqrt 2 .2}} = 25\sqrt 2 \Omega \);
Giải hệ
\(\left\{ \matrix{
{2.25^2} = {r^2} + Z_L^2 \hfill \cr
{{{Z_L}} \over r} = \sqrt 3 \hfill \cr} \right.\)
=>\({Z_L} = 12,5\sqrt 6 \Omega \)
Câu hỏi 7 :
Đặt điện áp xoay chiều vào hai đầu đoạn mạch có R,L,C mắc nối tiếp. Biết R = 10Ω, cuộn cảm thuần có L = 0,1/π (H), tụ điện có C = 5.10-4/π (F) và điện áp giữa hai đầu cuộn cảm thuần là \({u_L} = 20\sqrt {2.} \cos (100\pi t + {\pi \over 2})(V)\) . Biểu thức điện áp giữa hai đầu đoạn mạch là:
- A \(u = 40.cos(100\pi t + \pi /4)V\)
- B \(u = 40.cos(100\pi t - \pi /4)V\)
- C \(u = 40\sqrt 2 .cos(100\pi t + \pi /4)V\)
- D \(u = 40\sqrt 2 .cos(100\pi t - \pi /4)V\)
Đáp án: B
Phương pháp giải:
Sử dụng định luật Ôm và viết biểu thức điện áp
Lời giải chi tiết:
R = 10Ω; \({Z_L} = \omega L = 100\pi .{{0,1} \over \pi } = 10\Omega ;{Z_C} = {1 \over {\omega C}} = {1 \over {100\pi {{.5.10}^{ - 4}}{1 \over \pi }}} = 20\Omega \)
\(I = {{{U_L}} \over {{Z_L}}} = {{20} \over {10}} = 2A\)
U = I.Z = \(2.\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} = 2.\sqrt {{{10}^2} + {{(10 - 20)}^2}} = 20\sqrt 2 V\)
\(\tan \varphi = {{{Z_L} - {Z_C}} \over R} = - 1 \Rightarrow \varphi = {{ - \pi } \over 4}\)
\( \Rightarrow u = 20\sqrt 2 .\sqrt 2 .cos(100\pi t - {\pi \over 4})V = 40.cos(100\pi t - {\pi \over 4})V\)
Câu hỏi 8 :
Cho mạch điện RLC mắc nối tiếp, tụ điện có điện dung C thay đổi. Điều chỉnh điện dung của tụ sao cho điện áp hiệu dụng của tụ đạt giá trị cực đại. Khi đó điện áp hiệu dụng trên R = 75V và khi điện áp tức thời hai đầu mạch là V thì điện áp tức thời của đoạn mạch RL là V. Điện áp hiệu dụng của đoạn mạch là
- A \(75\sqrt 6 \) V
- B 150 V
- C \(150\sqrt 2 \) V
- D \(75\sqrt 3 \) V
Đáp án: B
Phương pháp giải:
Sử dụng lí thuyết mạch điện có diện dung thay đổi
Áp dụng hệ thức lượng trong tam giác vuông
Lời giải chi tiết:
Điều chỉnh điện dung để UC đạt cực đại thì điện áp uRLvuông pha với u nên : \({{{u^2}} \over {U_0^2}} + {{u_{LR}^2} \over {U_{RL}^2}} = 1\)(1)
Mặt khác theo hệ thức lượng trong tam giác vuông ta có:\({1 \over {U_{0R}^2}} = {1 \over {U_0^2}} + {1 \over {U_{0RL}^2}}\) (2)
Từ 1 và 2 ta có: \(U_0^2 = {{{u^2} - u_{lR}^2} \over {1 - {{u_{LR}^2} \over {U_{LR}^2}}}} = 45000 \Rightarrow U = {{{U_0}} \over {\sqrt 2 }} = 150V\)
Câu hỏi 9 :
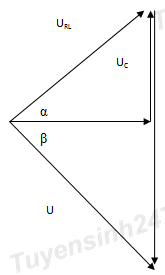
Đặt điện áp xoay chiều u = U0 cos\({{2\pi } \over T}t + \varphi \)) (V) vào hai đầu đoạn mạch AB như hình bên. Biết R = r. Đồ thị biểu diễn điện áp uAM và uMB như hình vẽ bên cạnh. Giá trị của U0 bằng
- A 84,85 V.
- B 75,89V
- C 107,33V
- D 120V
Đáp án: B
Phương pháp giải:
Vẽ giản đồ vec tơ của mạch điện, sử dụng các tính chất hình học
Lời giải chi tiết:
Từ đồ thị ta thấy được các giá trị U0AN = U0MB = 60V
Tại thời điểm ban đầu t = 0, thì điện áp trên đoạn AN = 0, điện áp trên đoạn MB đạt cực tiểu (ở biên âm), dao động với cùng chu kì, nên ta thấy được điện áp trên đoạn mạch MB trễ pha so với điện áp trên đoạn mạch AN một góc là π/2. Hay điện áp tức thời trên hai đoạn mạch này vuông pha với nhau.
Mặt khác R = r nên ta có UR = Ur.
Ta vẽ được giản đồ vecto như sau:
Dễ dàng chứng minh được hai tam giác OMN bằng với tam giác BMA theo trường hợp cạnh huyền và góc vuông (ON = AB; góc O = góc B)
Từ đó suy ra được : r = R = ZL = ZC /3
\({U_{R0}} = {U_{r0}} = {{60} \over {\sqrt 5 }}V\)
\(U_0^2 = {\left( {2{U_{r0}}} \right)^2} + {(2{U_{r0}})^2} = {{{{8.60}^2}} \over 5} \Rightarrow {U_0} = {{120\sqrt 2 } \over {\sqrt 5 }} = 75,98V\)
Câu hỏi 10 :
Cho đoạn mạch xoay chiều có R, L, C mắc nối tiếp, cuộn dây thuần cảm, tụ điện có điện dung C thay đổi được. Biết điện áp hiệu dụng hai đầu mỗi phần tử R, L, C tương ứng lần lượt là UR = 80V; UL = 240V và UC = 160V. Thay đổi điện dung C để điện áp hiệu dụng hai đầu C là UC’ = 100V thì điện áp hiệu dụng hai đầu điện trở là
- A 72,8V
- B 50,3V
- C 40,6V
- D 64,4V
Đáp án: D
Phương pháp giải:
Mạch RLC có C biến thiên
Lời giải chi tiết:
\({U_{AB}} = 80\sqrt 2 (V);{U_L} = 3{U_R} \Rightarrow {U_{AB}}^2 = U_R^2 + {(3{U_R} - {U_C})^2} \to {(80\sqrt 2 )^2} = U_R^2 + {(3{U_R} - 100)^2} \to {U_R} = 64,4V\)
Câu hỏi 11 :
Đặt điện áp \(u = {U_0}\cos (\omega t)\) vào hai đầu đoạn mạch có R, L, C mắc nối tiếp thì cường độ dòng điện chạy trong đoạn mạch là \(i = I\sqrt 2 \cos (\omega t + \varphi )\) với \(0 < \varphi < {\pi \over 2}\). Giữ nguyên \({U_0},\omega ,R,L\) giảm dần điện dung C của tụ điện thì giá trị I
.
- A giảm xuống rồi tăng lên.
- B luôn giảm dần.
- C luôn tăng dần.
- D tăng lên rồi giảm xuống
Đáp án: B
Câu hỏi 12 :
Đặt điện áp \(u = 100\sqrt 2 \cos \left( {100\pi + {\pi \over 6}} \right)V\) vào hai đầu đoạn mạch chỉ chứa một hoặc hai phần tử gồm điện trở thuần, cuộn dây hoặc tụ điện. Cường độ dòng điện qua đoạn mạch có biểu thức là \(i = 5\sqrt 2 \cos \left( {100\pi t - {\pi \over 6}} \right)A\). Phần tử trong đoạn mạch là
- A điện trở thuần R = 10Ω và tụ điện có điện dung \(C = {{{{10}^{ - 3}}} \over {\sqrt 3 \pi }}F\)
- B cuộn dây có điện trở r = 10Ω và độ tự cảm \(L = {{\sqrt 3 } \over {10\pi }}H\)
- C cuộn dây có điện trở \(r = 10\sqrt 3 \Omega \) và độ tự cảm \(L = {1 \over {10\pi }}H\)
- D điện trở thuần R = 10Ω và cuộn cảm thuần có độ tự cảm \(L = {1 \over {10\pi }}H\)
Đáp án: B
Phương pháp giải:
Sử dụng lí thuyết về mạch điện xoay chiều và công thức tính độ lệch pha giữa u và u
Lời giải chi tiết:
Độ lệch pha giữa điện áp và dòng điện là: \(\varphi = {\pi \over 3}\)
\(\to \tan \varphi = {{{Z_L}} \over r} = \sqrt 3 \to {Z_L} = \sqrt 3 r \to Z = 2r = {U \over I} = 20 \to r = 10;{Z_L} = 10\sqrt 3 \to L = {{\sqrt 3 } \over {10\pi }}H\)
Câu hỏi 13 :
Đặt điện áp \(u = 100\cos (100\pi t)V\) vào hai đầu đoạn mạch gồm điện trở thuần, cuộn dây thuần cảm có độ tự cảm \(L = {1 \over \pi }H\) và tụ điện có điện dung C thay đổi được. Cường độ dòng điện hiệu dụng trong mạch đạt giá trị cực đại khi
- A \(C = \pi {.10^{ - 4}}F\)
- B \(C = {{{{10}^{ - 4}}} \over \pi }\mu F\)
- C \(C = {{{{10}^{ - 4}}} \over \pi }F\)
- D \(C = \pi {.10^{ - 4}}\mu F\)
Đáp án: C
Phương pháp giải:
Điều kiện xảy ra cộng hưởng điện
Lời giải chi tiết:
Dòng điện đạt giá trị cực đại khi xảy ra cộng hưởng điện:
\({Z_C} = {Z_L} = 100 \to C = {1 \over {\omega {Z_C}}} = {{{{10}^{ - 4}}} \over \pi }F\)
Câu hỏi 14 :
Cho mạch điện có R, L, C mắc nối tiếp, cuộn cảm thuần có độ tự cảm L thay đổi đượC. Điện áp xoay chiều giữa hai đầu đoạn mạch luôn ổn định. Thay đổi L, khi L = L1 thì điện áp hiệu dụng giữa hai bản tụ điện có giá trị lớn nhất, điện áp hiệu dụng giữa hai đầu R bằng 220V. Khi L = L2 thì điện áp hiệu dụng giữa hai đầu cuộn cảm có giá trị lớn nhất và bằng 275V, điện áp hiệu dụng giữa hai đầu R bằng 132V và điện áp hiệu dụng giữa hai bản tụ điện là
- A 457V
- B 96V
- C 99V
- D 451V
Đáp án: C
Phương pháp giải:
Mạch RLC mắc nối tiếp có L thay đổi
Lời giải chi tiết:
Khi \(L = {L_1} \to {U_{C\max }} \to {U_R} = 220V = U\)
Khi \(L = {L_2} \to {U_{L\max }} \to {U_R} = 132V\)
=> \({U_L} = U{{\sqrt {U_R^2 + U_C^2} } \over {{U_R}}} \to {U_C} = 99V\)
Câu hỏi 15 :
Một đoạn mạch gồm điện trở thuần R, cuộn cảm thuần có hệ số tự cảm L và tụ điện có điện dung C mắc nối tiếp. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có giá trị hiệu dụng U và tần số góc ω không đổi thì cường độ dòng điện hiệu dụng trong mạch là I. Nếu nối tắt hai bản tụ điện thì cường độ dòng điện hiệu dụng trong mạch vẫn bằng I. Điều nào sau đây là đúng ?
- A ω2LC = 0,5
- B ω2LC = 2
- C ω2LC = 1 + ωRC
- D ω2LC = 1 - ωRC
Đáp án: A
Phương pháp giải:
Cường độ dòng điện hiệu dụng I = U/Z
Lời giải chi tiết:
Đoạn mạch gồm RLC mắc nối tiếp : \(I = {U \over {\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\) (1)
Khi nối tắt tụ : \(I = {U \over {\sqrt {{R^2} + Z_L^2} }}\) (2)
Từ (1) và (2)
\( \Rightarrow {U \over {\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = {U \over {\sqrt {{R^2} + Z_L^2} }} \Rightarrow \left\{ \matrix{
{Z_L} - {Z_C} = {Z_L}(loai) \hfill \cr
{Z_L} - {Z_C} = - {Z_L} \hfill \cr} \right. \Rightarrow 2{Z_L} = {Z_C} \Leftrightarrow 2\omega L = {1 \over {\omega C}} \Rightarrow {\omega ^2}LC = 0,5\)
Câu hỏi 16 :
Đoạn mạch AB gồm hai đoạn mạch AM và MB nối tiếp nhau. Trên đoạn AM chứa điện trở \(R = 30\sqrt 3 \Omega \) và tụ điện, trên đoạn MB chứa cuộn dây thuần cảm có hệ số tự cảm thay đổi được. Đặt vào hai đầu A, B một điện áp \(u = U\sqrt 2 c{\rm{os}}\left( {100\pi t} \right)\left( V \right)\) và điều chỉnh hệ số tự cảm sao cho điện áp hiệu dụng ở hai đầu cuộn cảm đạt cực đại. Biết rằng khi đó điện áp hiệu dụng ở hai đầu đoạn mạch AM trễ pha 2π/3 so với điện áp ở hai đầu của đoạn mạch MB. Điện dung của tụ điện có giá trị là
- A \({{{{10}^{ - 3}}} \over {3\pi }}F\)
- B \({{{{10}^{ - 3}}} \over {6\pi }}F\)
- C \({{{{10}^{ - 3}}} \over {3\pi \sqrt 3 }}F\)
- D \({{{{2.10}^{ - 3}}} \over {3\pi }}F\)
Đáp án: A
Phương pháp giải:
Sử dụng giản đồ vecto
Lời giải chi tiết:
Có:
\(\eqalign{
& {{{Z_C}} \over R} = {1 \over {\sqrt 3 }} \Rightarrow R = \sqrt 3 {Z_C} \Rightarrow {Z_L} = 4{Z_C} \cr
& \Rightarrow {Z_C} = 30\Omega = {1 \over {\omega C}} \Rightarrow C = {1 \over {\omega {Z_C}}} = {1 \over {100\pi .30}} \Rightarrow C = {{{{10}^{ - 3}}} \over {3\pi }}F \cr} \)
Câu hỏi 17 :
Đặt điện áp xoay chiều u = 100 cos(wt) V vào hai đầu mạch gồm điện trở R nối tiếp với tụ C có ZC = R. Tại thời điểm điện áp tức thời trên điện trở là \(50\sqrt 3 V\) và đang tăng thì điện áp tức thời trên tụ có giá trị là
- A 50 \(\sqrt 3 \)V.
- B - 50 \(\sqrt 3 \)V.
- C 50V.
- D -50V.
Đáp án: D
Phương pháp giải:
uC trễ pha hơn uR góc π/2
Sử dụng đường tròn lượng giác
Lời giải chi tiết:
Ta có:
\(\left\{ \matrix{
{Z_C} = R \Rightarrow {U_{0C}} = {U_{0R}} \hfill \cr
U_0^2 = U_{0C}^2 + U_{0R}^2 = {\left( {100\sqrt 2 } \right)^2} \hfill \cr} \right. \Rightarrow {U_{0C}} = {U_{0R}} = 100V\)
Do uC trễ pha hơn uR góc π/2, biểu diễn trên đường tròn lượng giác ta có:
=> Điện áp tức thời trên tụ là uC = -50V
Câu hỏi 18 :
Đặt điện áp u = 220cos100πt (V) vào hai đầu đoạn mạch gồm một bóng đèn dây tóc loại 110V – 50W mắc nối tiếp với một tụ điện có điện dung C thay đổi được. Điều chỉnh C để đèn sáng bình thường. Độ lệch pha giữa cường độ dòng điện và điện áp ở hai đầu đoạn mạch lúc này là:
- A π/2
- B π/3
- C π/6
- D π/4
Đáp án: D
Phương pháp giải:
\(c{\rm{os}}\varphi = {R \over Z} = {{{U_R}} \over U}\)
(φ là độ lệch pha giữa u và i)
Lời giải chi tiết:
Khi đèn sáng bình thường thì UR = 110V \( \Rightarrow c{\rm{os}}\varphi = {{{U_R}} \over U} = {{110} \over {110\sqrt 2 }} = {1 \over {\sqrt 2 }} \Rightarrow \varphi = {\pi \over 4}\)
Câu hỏi 19 :
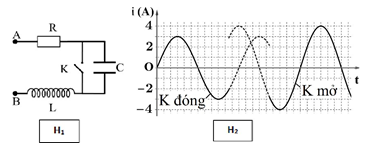
Đặt điện áp xoay chiều u = U0cos(ωt + φ) vào hai đầu đoạn mạch AB gồm điện trở R = 24Ω, tụ điện và cuộn cảm thuần mắc nối tiếp (hình H1). Ban đầu khóa K đóng, sau đó khóa K mở. Hình H2 là đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện i trong đoạn mạch vào thời gian t. Giá trị của U0 gần nhất với giá trị nào sau đây?
- A 127 V.
- B 212 V.
- C 255 V.
- D 170 V.
Đáp án: A
Phương pháp giải:
Sử dụng công thức I0 = U0/Z , độ lệch pha tanφ = (ZL – ZC)/R kết hợp kĩ năng đọc đồ thị
Lời giải chi tiết:
\(\eqalign{
& {{U_0^2} \over {{3^2}}} = R_0^2 + Z_L^2 \Rightarrow Z_L^2 = {{U_0^2} \over {{3^2}}} - 5,76 \cr
& {{U_0^2} \over {{4^2}}} = R_0^2 + {\left( {{Z_L} - {Z_C}} \right)^2} \Rightarrow {\left( {{Z_L} - {Z_C}} \right)^2} = {{U_0^2} \over {{4^2}}} - 5,76 \cr
& {R^2} = {Z_L}\left( {{Z_L} - {Z_C}} \right) \Rightarrow {{{R^2}} \over {Z_L^2}} = {{{Z_L} - {Z_C}} \over {{Z_L}}} \Rightarrow {{{{U_0^2} \over {{4^2}}} - 5,76} \over {{{U_0^2} \over {{3^2}}} - 5,76}} = {\left( {{{{R^2}} \over {Z_L^2}}} \right)^2} \cr} \)
\(\eqalign{
& \Rightarrow \left( {{{U_0^2} \over {{4^2}}} - 5,76} \right)\left( {{{U_0^2} \over {{3^2}}} - 5,76} \right) = {R^4}\left( {{{U_0^2} \over {{3^2}}} - 5,76} \right) \Rightarrow \left( {{{U_0^2} \over {{4^2}}} - 5,76} \right)\left( {{{U_0^2} \over {{3^2}}} - 5,76} \right) = {R^4} \cr
& \Rightarrow {{U_0^4} \over {{3^2}{{.4}^2}}} - 5,76\left( {{{U_0^2} \over {{3^2}}} + {{U_0^2} \over {{4^2}}}} \right) = 0 \Rightarrow {U_0} = R\sqrt {{3^2} + {4^2}} = 120V \cr} \)
Câu hỏi 20 :
Đặt hiệu điện thế u = U0sinωt (U0 không đổi) vào hai đầu đoạn mạch RLC không phân nhánh. Biết điện trở thuần của mạch không đổi. Khi có hiện tượng cộng hưởng điện trong đoạn mạch, phát biểu nào sau đây sai?
- A Cường độ hiệu dụng của dòng điện trong mạch đạt giá trị lớn nhất.
- B Hiệu điện thế tức thời ở hai đầu đoạn mạch cùng pha với hiệu điện thế tức thời ở hai đầu điện trở R.
- C Cảm kháng và dung kháng của đoạn mạch bằng nhau.
- D Hiệu điện thế hiệu dụng ở hai đầu điện trở R nhỏ hơn hiệu điện thế hiệu dụng ở hai đầu đoạn mạch.
Đáp án: D
Lời giải chi tiết:
Đáp án D
+ Khi xảy ra hiện tượng cộng hưởng thì hiệu điện thế hai đầu đoạn mạch đúng bằng hiệu điện thế hai đầu R → D sai.
Câu hỏi 21 :
Đặt hiệu điện thế u = U0sinωt với ω , U0 không đổi vào hai đầu đoạn mạch RLC không phân nhánh. Hiệu điện thế hiệu dụng hai đầu điện trở thuần là 80 V, hai đầu cuộn dây thuần cảm (cảm thuần) là 120 V và hai đầu tụ điện là 60 V. Hiệu điện thế hiệu dụng ở hai đầu đoạn mạch này bằng
- A 140 V.
- B 260 V.
- C 100 V.
- D 220 V.
Đáp án: C
Lời giải chi tiết:
Đáp án C
+ Hiệu điện thế hiệu dụng ở hai đầu đoạn mạch \(U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} = \sqrt {{{80}^2} + {{\left( {120 - 60} \right)}^2}} = 100V\)
Câu hỏi 22 :
Đặt điện áp u = Uocosωt vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, tụ điện và cuộn cảm thuần có độ tự cảm L thay đổi được. Biết dung kháng của tụ điện bằng \(\sqrt 3 \)R. Điều chỉnh L để điện áp hiệu dụng giữa hai đầu cuộn cảm đạt cực đại, khi đó:
- A trong mạch có cộng hưởng điện.
- B điện áp giữa hai đầu điện trở lệch pha π/6 so với điện áp giữa hai đầu đoạn mạch.
- C điện áp giữa hai đầu cuộn cảm lệch pha π/6 so với điện áp giữa hai đầu đoạn mạch.
- D điện áp giữa hai đầu tụ điện lệch pha π/6 so với điện áp giữa hai đầu đoạn mạch
Đáp án: B
Phương pháp giải:
sử dụng giản đồ vectơ trong dòng điện xoay chiều
Lời giải chi tiết:
Đáp án B
+ Khi xảy ra cực đại của điện áp hiệu dụng trên cuộn dây, ta có u vuông pha với uRC.
Mặc khác .\(\tan {\varphi _{RC}} = - {{{Z_C}} \over R} = - \sqrt 3 = > {\varphi _{RC}} = - {60^0}\)
+ Từ hình vẽ, ta thấu rằng điện áp hai đầu điện trở lệch pha 300so với điện áp hai đầu mạch.
Câu hỏi 23 :
Cho ba linh kiện gồm điện trở thuần R = 60 Ω, cuộn cảm thuần L và tụ điện C. Lần lượt đặt điện áp xoay chiều có giá trị hiệu dụng U vào hai đầu đoạn mạch nối tiếp RL hoặc RC thì biểu thức cường độ dòng điện trong mạch lần lượt là i1 = \(\sqrt 2 \)cos(100πt - π/12) (A) và i2 =\(\sqrt 2 \)cos(100πt + 7π/12) (A). Nếu đặt điện áp trên vào hai đầu đoạn mạch RLC nối tiếp thì dòng điện trong mạch có biểu thức
- A i = \(2\sqrt 2 \)cos(100πt + π/3) (A).
- B i = 2cos(100πt + π/3)(A).
- C i = 2cos(100πt + π/4) (A).
- D i = \(2\sqrt 2 \)cos(100πt + π/4) (A).
Đáp án: D
Lời giải chi tiết:
Đáp án D
Theo đề
${I_{01}} = {I_{02}} \Rightarrow {Z_{RL}} = {Z_{RC}} \Rightarrow \left\{ \matrix{
{{\rm{\varphi }}_{\rm{1}}}{\rm{ = - }}{{\rm{\varphi }}_{\rm{2}}}\left( 1 \right) \hfill \cr
{Z_L} = {Z_C} \hfill \cr} \right.$
Mặt khác
$\left. \matrix{
{{\rm{\varphi }}_{\rm{u}}}{\rm{ - }}{{\rm{\varphi }}_{{i_1}}}{\rm{ = }}{{\rm{\varphi }}_{\rm{1}}}\left( 2 \right) \hfill \cr
{{\rm{\varphi }}_{\rm{u}}}{\rm{ - }}{{\rm{\varphi }}_{{i_2}}}{\rm{ = }}{{\rm{\varphi }}_{\rm{2}}} \hfill \cr} \right\}\mathop \Rightarrow \limits^{\left( 1 \right)} {{\rm{\varphi }}_{\rm{u}}} = {{{{\rm{\varphi }}_{{i_1}}} + {{\rm{\varphi }}_{{i_2}}}} \over 2} = {{\rm{\pi }} \over {\rm{4}}}\left( 3 \right)$
Từ $\left( 2 \right),\left( 3 \right) \Rightarrow {{\rm{\varphi }}_{\rm{1}}} = {{\rm{\pi }} \over {\rm{3}}} \Rightarrow {{{Z_L}} \over R} = \sqrt 3 \Rightarrow {Z_L} = 60\sqrt 3 \left( {\rm{\Omega }} \right)$
$ \Rightarrow {U_0} = {I_{01}}{Z_{RL}} = 120\sqrt 2 \left( V \right)$
Khi $RL{C_{}}nt \to $cộng hưởng: \(i = {{{U_0}} \over R}\cos \left( {100\pi t + {\varphi _u}} \right) = 2\sqrt 2 \cos \left( {100\pi t + {\pi \over 4}} \right)\)
Câu hỏi 24 :
Đặt điện áp \(u = 200\sqrt 2 \cos \left( {100\pi t} \right)\) V vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần 100 Ω và cuộn cảm thuần có độ tự cảm \({1 \over \pi } H\). Biểu thức cường độ dòng điện trong đoạn mạch là
- A \(i = 2\sqrt 2 \cos \left( {100\pi t + {\pi \over 4}} \right)A\)
- B \(i = 2\cos \left( {100\pi t - {\pi \over 4}} \right)A\)
- C \(i = 2\cos \left( {100\pi t + {\pi \over 4}} \right)A\)
- D \(i = 2\sqrt 2 \cos \left( {100\pi t - {\pi \over 4}} \right)A\)
Đáp án: B
Lời giải chi tiết:
Đáp án B
+ Cảm kháng của cuộn dây \({{\rm{Z}}_L} = L\omega = 100\,\,\Omega \,.\)
Biểu diễn phức dòng điện trong mạch
\(\overline i = {{\overline u } \over {\overline Z }} = {{200\sqrt 2 \angle 0} \over {100 + 100i}} = 2\angle - 45^\circ \to i = 2\cos \left( {100\pi t - {\pi \over 4}} \right)\,\,A.\)
Câu hỏi 25 :
Đặt điện áp xoay chiều u = U0cosωtV vào hai đầu đoạn mạch chỉ chứa cuộn dây thuần cảm. Khi điện áp ở hai đầu cuộn dây là \(60\sqrt 6 \) V thì cường độ dòng điện trong mạch là \(2\sqrt 2 \)A, khi điện áp ở hai đầu cuộn dây là V thì dòng điện trong mạch là \(2\sqrt 6 \)A. Cảm kháng cuộn dây là
- A \(20\sqrt 2 \Omega \)
- B \(40\sqrt 3 \Omega \)
- C 40 Ω.
- D 30 Ω.
Đáp án: D
Phương pháp giải:
Hệ thức vuông pha giữa u và i trong mạch chỉ chứa cuộn cảm thuần \({\left( {{u \over {{I_0}{Z_L}}}} \right)^2} + {\left( {{i \over {{I_0}}}} \right)^2} = 1\)
Lời giải chi tiết:
Đáp án D
+ Với đoạn mạch chỉ chứa cuộn cảm thuần thì dòng điện trong mạch luôn vuông pha với điện áp, do đó ta có công thức độc lập thời gian:
+
\({\left( {{u \over {{I_0}{Z_L}}}} \right)^2} + {\left( {{i \over {{I_0}}}} \right)^2} = 1 \Rightarrow \left\{ \matrix{
{\left( {{{60\sqrt 6 } \over {{Z_L}}}} \right)^2} + {\left( {2\sqrt 2 } \right)^2} = {I_0} \hfill \cr
{\left( {{{60\sqrt 2 } \over {{Z_L}}}} \right)^2} + {\left( {2\sqrt 6 } \right)^2} = {I_0} \hfill \cr} \right. \Rightarrow {Z_L} = \sqrt {{{{{\left( {60\sqrt 6 } \right)}^2} - {{\left( {60\sqrt 2 } \right)}^2}} \over {{{\left( {2\sqrt 6 } \right)}^2} - {{\left( {2\sqrt 2 } \right)}^2}}}} = 30\,\,\Omega \,.\)
Câu hỏi 26 :
Trong đoạn mạch xoay chiều chỉ có tụ điện, (điện áp hiệu dụng ở hai đầu mạch không đổi) nếu đồng thời tăng tần số của điện áp lên 4 lần và giảm điện dung của tụ điện 2 lần thì cường độ hiệu dụng qua mạch
- A tăng 2 lần.
- B tăng 3 lần.
- C giảm 2 lần.
- D giảm 4 lần.
Đáp án: A
Lời giải chi tiết:
Đáp án A
+ Tăng tần số của dòng điện lên 4 lần và giảm điện dung đi 2 lần tăng 2 lần → dòng điện hiệu dụng tăng 2 lần.
Câu hỏi 27 :
Trong một hộp kín chứa 2 trong 3 phần tử : điện trở thuần, cuộn cảm thuần và tụ điện. Hai phần tử trong hộp mắc nối tiếp và 2 đầu nối ra ngoài là M và N. Đặt vào 2 đầu M, N điện áp xoay chiều \(u = 120\sqrt 2 \cos \left( {100\pi t + {\pi \over 3}} \right)V\) thì cường độ dòng điện chạy trong hộp có biểu thức \(i = 3\sqrt 2 \cos \left( {100\pi t + {\pi \over 6}} \right)A\). Các phần tử trong hộp là
- A điện trở \(R = 20\Omega \), tụ điện có \(C = {{{{10}^{ - 3}}} \over {2\sqrt 3 \pi }}F\)
- B điện trở \(R = 20\Omega \), cuộn dây \(L = {1 \over {5\pi \sqrt 3 }}F\).
- C điện trở \(R = 20\sqrt 3 \,\Omega \), tụ điện có \(C = {{{{10}^{ - 3}}} \over {2\pi }}F\)
- D điện trở \(R = 20\sqrt 3 \,\Omega \), cuộn dây có \(L = {1 \over {5\pi }}F\)
Đáp án: D
Lời giải chi tiết:
Cường độ dòng điện: \(i = 3\sqrt 2 \cos \left( {100\pi t + {\pi \over 6}} \right)A\)
→ Điện áp sớm pha hơn dòng điện một góc \(30^\circ \to \) mạch chứa cuộn cảm thuần và điện trở thuần:
\(\eqalign{
& \tan {30^0} = {{{Z_L}} \over R} \to R = \sqrt 3 {Z_L} \to Z = 2{Z_L} = 40\Omega \to {Z_L} = 20\Omega \Rightarrow L = {1 \over {5\pi }}H \cr
& \Rightarrow R = 20\sqrt 3 \Omega \cr} \)
Câu hỏi 28 :
Đoạn mạch điện xoay chiều gồm một cuộn dây dẫn có điện trở r không đổi, độ tự cảm \(L = {{\sqrt 3 } \over {2\pi }}H\) mắc nối tiếp với tụ điện có điện dung thay đổi được. Đặt vào hai đầu đoạn mạch trên một điện áp xoay chiều có dạng \(u = U\sqrt 2 \cos \left( {100\pi t + {\pi \over 6}} \right)V\). Để điện áp giữa hai đầu cuộn dây dẫn cực đại thì điện dung của tụ điện có giá trị là :
- A \({{{{2.10}^{ - 4}}} \over {\sqrt 3 \pi }}F\)
- B \({{{{10}^{ - 4}}} \over {\sqrt 3 \pi }}F\)
- C \({{\sqrt 3 {{.10}^{ - 4}}} \over \pi }F\)
- D \({{{{5.10}^{ - 4}}} \over {\sqrt 3 \pi }}F\)
Đáp án: A
Phương pháp giải:
áp dụng điều kiện xảy ra cộng hưởng trong mạch điện xoay chiều
Lời giải chi tiết:
Đáp án A
+ Để điện áp hai đầu cuôn dây dẫn cực đại thì mạch xảy ra cộng hưởng
\( \to C = {1 \over {L{\omega ^2}}} = {1 \over {{{\sqrt 3 } \over {2\pi }}{{\left( {100\pi } \right)}^2}}} = {{{{2.10}^{ - 4}}} \over {\sqrt 3 \pi }}F.\)
Câu hỏi 29 :
Cho mạch điện như hình vẽ, cuộn dây thuần cảm, r = 0. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có giá trị cực đại \({U_0} = 100\sqrt 6 V\), tần số f = 50 Hz. Khi K mở hoặc đóng, thì đồ thị cường độ dòng điện qua mạch theo thời gian tương ứng là im và id được biểu diễn như hình bên. Điện trở các dây nối rất nhỏ. Giá trị của R bằng
- A 100 Ω.
- B \(100\sqrt 3 \Omega \)
- C \(50\sqrt 3 \Omega \)
- D 50 Ω.
Đáp án: D
Phương pháp giải:
Sử dụng giản đồ vecto và các công thức lượng giác, hệ số công suất.
Lời giải chi tiết:
Từ đồ thị ta thấy
\(\eqalign{
& {I_d} = {{\sqrt 6 } \over {\sqrt 2 }} = \sqrt 3 A \Rightarrow {Z_d} = {U \over {{I_d}}} = {{100\sqrt 3 } \over {\sqrt 3 }} = 100\Omega \cr
& {I_m} = {{3\sqrt 2 } \over {\sqrt 2 }} = 3A \Rightarrow {Z_m} = {U \over {{I_m}}} = {{100\sqrt 3 } \over 3} = {{100} \over {\sqrt 3 }}\Omega \cr} \)
Khi đóng và mở khóa K thì cường độ dòng điện lệch pha nhau 1 góc là 900.
Ta vẽ trên một giản đồ vecto khi đóng và mở khóa K:
Từ công thức tính hệ số công suất ta có:
\(\eqalign{
& \cos {\varphi _d} = {R \over {{Z_d}}};\cos {\varphi _m} = {R \over {{Z_m}}};{\varphi _d} + {\varphi _m} = {\pi \over 2} \Rightarrow \cos {\varphi _d} = \sin {\varphi _m} = \sqrt {1 - {{\cos }^2}{\varphi _m}} \cr
& \Rightarrow {\left( {{R \over {{{100} \over {\sqrt 3 }}}}} \right)^2} = 1 - {\left( {{R \over {100}}} \right)^2} \Leftrightarrow {{3.{R^2}} \over {{{100}^2}}} = 1 - {{{R^2}} \over {{{100}^2}}} \Leftrightarrow 4.{R^2} = {100^2} \Rightarrow R = \sqrt {{{{{100}^2}} \over 4}} = 50\Omega \cr} \)
Câu hỏi 30 :
Khi đặt điện áp \(u = 220\sqrt 2 \cos \left( {100\pi t - {\pi \over 6}} \right)\,V\) vào hai đầu một hộp X chứa 2 trong 3 linh kiện điện là R0, L0, C0 mắc nối tiếp thì cường độ dòng điện qua đoạn mạch có biểu thức \(i = 2\sqrt 2 \cos \left( {100\pi t + {\pi \over 6}} \right)\,A\). Nếu mắc hộp X nối tiếp với cuộn cảm thuần có \(L = {{\sqrt 3 } \over \pi }{\rm H}\) rồi mắc vào điện áp trên thì cường độ dòng điện qua đoạn mạch là
- A \(i = 2\cos \left( {100\pi t + {\pi \over 3}} \right)A\)
- B \(i = 2\sqrt 2 \cos \left( {100\pi t + {\pi \over 2}} \right)A\)
- C \(i = 2\cos \left( {100\pi t - {\pi \over 3}} \right)A\)
- D \(i = 2\sqrt 2 \cos \left( {100\pi t - {\pi \over 2}} \right)A\)
Đáp án: D
Lời giải chi tiết:
Đáp án D
+ Ta thấy dòng điện qua X sớm pha hơn điện áp một góc \(60^\circ \leftrightarrow X\) chứa C0 và R0 với \({{\rm{Z}}_{C0}} = \sqrt 3 {R_0}.\)
+ Kết hợp với
\({{\text{Z}}_X} = \frac{{{U_X}}}{{{I_X}}} = \frac{{200}}{2} = 100\Omega \to \left\{ \begin{gathered}
{R_0} = 50 \hfill \\
{Z_{C0}} = 50\sqrt 3 \Omega \hfill \\
\end{gathered} \right.\)
+ Cảm kháng của cuộn dây \({{\rm{Z}}_L} = 100\sqrt 3 \,\,\Omega .\)
Dòng điện khi mắc thêm vào cuộn dây là \(\overline i = {{\overline u } \over {\overline Z }} = {{200\sqrt 2 \angle - 30} \over {50 + \left( {100\sqrt 3 - 50\sqrt 3 } \right)i}} = 2\sqrt 2 \angle - 90 \to i = 2\sqrt 3 \cos \left( {100\pi t - {\pi \over 2}} \right)\,\,A.\)
Câu hỏi 31 :
Đặt điện áp u = U0cos100πtV vào hai đầu đoạn mạch A, B gồm cuộn dây thuần cảm, có độ tự cảm \(L = {1 \over {4\pi }}H\) và tụ có điện dung \(C = {{400} \over {3\pi }}\mu F\) mắc nối tiếp. Tại thời điểm điện áp tức thời giữa hai đầu tụ điện bằng 120 V thì điện áp tức thời giữa hai đầu A, B có giá trị bằng
- A 80 V.
- B –160 V.
- C –80 V.
- D 160 V.
Đáp án: A
Lời giải chi tiết:
Đáp án A
+ Cảm kháng và dung kháng của đoạn mạch \({{\rm{Z}}_L} = 25\,\,\Omega ,\,\,{Z_C} = 75\,\,\Omega .\)
Tổng trở của mạch \({\rm{Z}} = \left| {{Z_L} - {Z_C}} \right| = \left| {25 - 75} \right| = 50\,\,\Omega .\)
+ Ta để ý rằng \({{\rm{Z}}_C} > {Z_L} \to \) u cùng pha với \({u_C}.\)
\( \to u = {Z \over {{Z_C}}}{u_C} = {{50} \over {75}}120 = 80\,\,V.\)
Câu hỏi 32 :
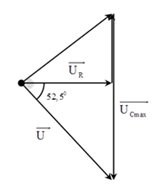
Đặt vào hai đầu đoạn mạch RLC mắc nối tiếp một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi. Biết R không đổi, cuộn thuần cảm có độ tự cảm L không đổi, điện dung của tụ điện thay đổi được. Khi điện dung C = C1 và C = C2 thì điện áp hiệu dụng hai đầu tụ điện có cùng giá trị, khi C = C1 thì điện áp u hai đầu đoạn mạch trễ pha hơn i một góc π/6 . Khi C = C2 thì điện áp u ở hai đầu đoạn mạch trễ pha hơn i một góc 5π/12 . Khi C = C0 thì điện áp hiệu dụng hai đầu tụ điện đạt giá trị cực đại là UCmax = 186 V, đồng thời khi đó điện áp hiệu dụng hai đầu R có giá trị gần nhất với giá trị nào sau đây?
- A 200 V.
- B 100 V.
- C 180 V.
- D 150 V.
Đáp án: B
Lời giải chi tiết:
Đáp án B
+ Với \({\varphi _1},\,\,{\varphi _2}\) và \({\varphi _0}\) là độ lệch pha giữa u và i ứng với \({C_1},\,\,{C_2},\,\,{C_0}\) . Ta có
\({\varphi _1} + {\varphi _2} = 2{\varphi _0}\) \(\to {\varphi _0} = - 52,5^\circ \)
+ Khi \(C = {C_0}\) điện áp hiệu dụng trên tụ cực đại thì \({u_{RL}}\) vuông pha với u.
+ Từ hình vẽ, ta có:
\(\left\{ \matrix{
U = {U_{C\max }}\sin \left| {{\varphi _0}} \right| \hfill \cr
{U_R} = U\cos \left| {{\varphi _0}} \right| \hfill \cr} \right. \to {U_R} = {{{U_{C\max }}} \over 2}\sin 2{\varphi _0} = {{186} \over 2}\sin \left| {2.\left( {52,5} \right)} \right| = 89\,\,V.\)
Câu hỏi 33 :
Đặt điện áp \(u = U\sqrt 2 \cos \left( {100\pi t} \right)\,V\) vào hai đầu đoạn mạch AB gồm điện trở R, cuộn dây thuần cảm L và C mắc nối tiếp. Biết R = 100 Ω, \(L = {1 \over {2\pi }}H,\,\,C = {{{{10}^{ - 3}}} \over {5\pi }}F\) điện áp hiệu dụng hai đầu điện trở thuần R = 200 V. Khi điện áp tức thời giữa hai đầu đoạn mạch AB có giá trị \( - 100\sqrt 6 \,V\) và có độ lớn đang tăng thì điện áp tức thời hai đầu tụ C có giá trị là
- A \(50\sqrt 2 V\)
- B \(-50\sqrt 6 V\)
- C \(50\sqrt 6 V\)
- D \(-50\sqrt 2 V\)
Đáp án: A
Lời giải chi tiết:
Đáp án A
+ Cảm kháng và dung kháng của đoạn mạch \({Z_L} = 50\,\,\Omega \), \({Z_C} = 50\,\,\Omega \to \) mạch xảy ra cộng hưởng \({U_C} = 0,5{U_R} = 100\,\,V\).
+ Điện áp ở hai đầu đoạn mạch sớm pha hơn điện áp trên tụ một góc \(0,5\pi\) rad.
Khi \(u = - {{\sqrt 3 } \over 2}{U_0} = - 100\sqrt 6 \) và có độ lớn đang tăng ->\({u_C} = {1 \over 2}{U_{0C}} = {1 \over 2}100\sqrt 2 = 50\sqrt 2 \,\,V.\)
Câu hỏi 34 :
Cho mạch điện gồm tụ điện C, điện trở R và hộp kín X mắc nối tiếp như hình vẽ. Hộp kín X là một trong ba phần tử: điện trở thuần, tụ điện, cuộn dây. Khi đặt vào hai đầu AB điện áp xoay chiều có giá trị hiệu dụng 130V thì hiệu điện thế hiệu dụng hai đầu AM và MB lần lượt là 50V và 120V. Hộp kín X là
- A tụ điện
- B cuộn dây không thuần cảm.
- C cuộn dây thuần cảm
- D điện trở thuần
Đáp án: B
Phương pháp giải:
Sử dụng công thức tính điện áp hiệu dụng
Lời giải chi tiết:
+ TH1: Hộp kín X là tụ điện => UMB = UCX = 120V
\( \Rightarrow \left\{ \matrix{
{U_{AB}} = U_R^2 + {\left( {{U_C} + 120} \right)^2} = {130^2} \hfill \cr
{U_{AM}} = U_R^2 + U_C^2 = {50^2} \hfill \cr} \right. \Rightarrow 240{U_C} + {120^2} = {130^2} - {50^2} \Rightarrow {U_C} = 0\)
=> Loại đáp án A
+ TH2: Hộp kín X là cuộn dây thuần cảm => UMB = ULX = 120V
\( \Rightarrow \left\{ \matrix{
{U_{AB}} = U_R^2 + {\left( {120 - {U_C}} \right)^2} = {130^2} \hfill \cr
{U_{AM}} = U_R^2 + U_C^2 = {50^2} \hfill \cr} \right. \Rightarrow {120^2} - 240{U_C} + = {130^2} - {50^2} \Rightarrow {U_C} = 0\)
=> Loại đáp án C
+ TH3: Hộp kín X là điện trở thuần => UMB = URX = 120V
\( \Rightarrow \left\{ \matrix{
{U_{AB}} = {\left( {{U_R} + 120} \right)^2} + U_C^2 = {130^2} \hfill \cr
{U_{AM}} = U_R^2 + U_C^2 = {50^2} \hfill \cr} \right. \Rightarrow 240{U_R} + {120^2} = {130^2} - {50^2} \Rightarrow {U_R} = 0\)
=> Loại đáp án D
=> Chọn B
Câu hỏi 35 :
Một đoạn mạch điện gồm một cuộn dây thuần cảm có độ tự cảm L mắc nối tiếaip với là các hằng số dương và không đổi . Điều chỉnh R để biến trở nhận hai giá trị R1 và R2 mà với hai giá trị đó thì điện áp giữa hai đầu đoạn mạch lệch pha so với cường độ dòng điện trong mạch với các góc tương ứng là α và β thỏa mãn \(\alpha + \beta = \frac{\pi }{2}\). Hệ thức nào sau đây đúng
- A \(\omega L = \sqrt {{R_1}{R_2}} \)
- B \(\omega L = {R_1} + {R_2}\)
- C \(\omega L = \frac{1}{2}\left( {{R_1} + {R_2}} \right)\)
- D \(2\omega L = {R_1} + {R_2}\)
Đáp án: A
Lời giải chi tiết:
Đáp án A
Theo bài ra ta có \(\alpha + \beta = \frac{\pi }{2}\)
Ta có
\(\left\{ \matrix{
\tan \alpha = {{{Z_L}} \over {{R_1}}} \hfill \cr
\tan \beta = {{{Z_L}} \over {{R_2}}} \hfill \cr} \right. = > \tan \alpha .\tan \beta = \tan \alpha = {{{Z_L}.{Z_L}} \over {{R_1}{R_2}}} = 1 = > \omega L = \sqrt {{R_1}{R_2}} \)
Câu hỏi 36 :
Cho đoạn mạch AB gồm cuộn dây thuần có điện trở thuần 100Ω và độ tự cảm \(\frac{1}{\pi }H\)mắc nối tiếp với tụ điện có điện dung \(\frac{{{{10}^{ - 4}}}}{{2\pi }}F\). Đặt vào hai đầu đoạn mạch AB một điện áp xoay chiều \({u_{AB}} = 200\cos 100\pi t(V)\). Khi điện áp tức thời giữa hai đầu đoạn mạch AB là\(100\sqrt 3 V\) và đang giảm thì điện áp tức thới giữa hai đầu cuộn dây là
- A -100 V và đang giảm
- B – 100 V và đang tăng
- C 100 V và đang giảm
- D 100 V và đang tăng
Đáp án: A
Lời giải chi tiết:
Đáp án A
Tổng trở của mạch là \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = \sqrt {{{100}^2} + \left( {100\pi .\frac{1}{\pi } - \frac{1}{{\frac{{{{10}^{ - 4}}.100\pi }}{{2\pi }}}}} \right)} = 100\sqrt 2 \Omega \)
Độ lệch pha giữa u và i được xác định bởi biểu thức \(\tan \varphi = \frac{{{Z_l} - {Z_C}}}{R} = \frac{{100 - 200}}{{100}} = - 1 = > \varphi = - \frac{\pi }{4}\)
Biểu thức cường độ dòng điện \(i = \sqrt 2 \cos \left( {100\pi t - \frac{\pi }{4}} \right)A\)
Độ lệch pha giữa ud và i được xác định bởi biểu thức \(\tan {\varphi _d} = \frac{{{Z_L}}}{R} = \frac{{100}}{{100}} = 1 = > {\varphi _d} = \frac{\pi }{4}\)
Biểu thức điện áp hai đầu cuộn dây là \({u_d} = \sqrt {{R^2} + Z_L^2} .{I_0}\cos \left( {100\pi t + \frac{\pi }{2}} \right) = 200\cos (100\pi t + \frac{\pi }{2})\)
Tại thời điểm t:
\(\eqalign{
& {u_{AB}} = 100\sqrt 3 = 200\cos 100\pi t = > t = {1 \over {600}}s \cr
& = > {u_d} = 200\cos \left( {100\pi t + {\pi \over 2}} \right) = 200\cos \left( {100\pi {1 \over {600}} + {\pi \over 2}} \right) = - 100V \cr} \)
Ta có \(t = \frac{1}{{600}}s \Leftrightarrow \frac{T}{{12}} \Leftrightarrow \frac{\pi }{6}\) biểu diễn trên đường tròn lượng giác ta thấy điện áp ở hai đầu cuộn dây đang giảm
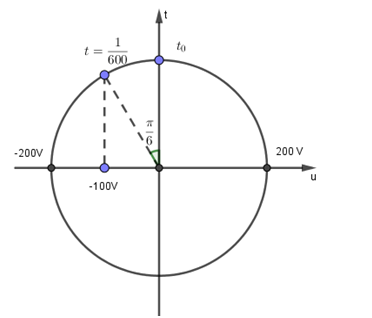
Câu hỏi 37 :
Đặt điện áp \(u = {U_0}{\rm{cos}}\left( {\omega t} \right)\left( V \right)\) vào hai đầu đoạn mạch nối tiếp gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Cảm kháng của đoạn mạch là \(R\sqrt 3 \), dung kháng của mạch là \(2R\sqrt 3 \). So với điện áp giữa hai đầu đoạn mạch thì cường độ dòng điện trong mạch
- A sớm pha π/6
- B sớm pha π/3
- C trễ pha π/6
- D trễ pha π/6
Đáp án: B
Phương pháp giải:
Áp dụng công thức tính độ lệch pha giữa u và i trong đoạn mạch RLC mắc nối tiếp: \(\tan \varphi = {{{Z_L} - {Z_C}} \over R}\)
Lời giải chi tiết:
Áp dụng công thức tính độ lệch pha giữa u và i trong đoạn mạch RLC mắc nối tiếp:
\(\eqalign{
& \tan \varphi = {{{Z_L} - {Z_C}} \over R} = {{R\sqrt 3 - 2R\sqrt 3 } \over R} = - \sqrt 3 \cr
& \Rightarrow \varphi = {\varphi _u} - {\varphi _i} = - {\pi \over 3} \cr} \)
Vậy i sớm pha hơn u góc π/3
Chọn B
Câu hỏi 38 :
Đặt điện áp xoay chiều \(u = {U_0}{\rm{cos}}\left( {\omega t} \right)\left( V \right)\) vào hai đầu đoạn mạch AB theo thứ tự gồm điện trở R = 90 Ω; cuộn dây không thuần cảm có r = 10 Ω và tụ điện có điện dung C thay đổi được. M là điểm nối giữa R và cuộn dây. Khi C = C1 thì điện áp hiệu dụng hai đầu đoạn mạch MB đạt giá trị cực tiểu bằng U1. Khi C = C2 = \({{{C_1}} \over 2}\) thì điện áp hiệu dụng trên tụ điện đạt giá trị cực đại bằng U2. Tỉ số \({{{U_2}} \over {{U_1}}}\) bằng:
- A \(9\sqrt 2 \)
- B \(\sqrt 2 \)
- C \(10\sqrt 2 \)
- D \(5\sqrt 2 \)
Đáp án: C
Lời giải chi tiết:
Ta có: \({({U_{MB}})_{min}} = {U_r} = {{U.r} \over {R + r}} = {U \over {10}} \Leftrightarrow {Z_{C1}} = {Z_L}\)
Khi : \({U_{C\max }} = > {Z_{C2}} = 2{Z_{C1}} = 2{Z_L} = {{{{(R + r)}^2} + Z_L^2} \over {{Z_L}}} \Rightarrow R + r = {Z_L} = 100{\rm{\Omega }}\)
Và có : \({U_{Cmax}} = {{U\sqrt {{{(R + r)}^2} + Z_L^2} } \over {R + r}} = U\sqrt 2 \)
Vậy tỉ số: \({{{U_{Cmax}}} \over {{{({U_{MB}})}_{min}}}} = 10\sqrt 2 \)
Câu hỏi 39 :
Đặt điện áp xoay chiều vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Biết R =10Ω, cuôn cảm thuần có L = l/(10π) (H), tụ điện có C = 10-3/2π (F) và điện áp giữa hai đầu cuộn cảm thuần là uL=\(20\sqrt 2 \cos (100\pi t + \pi /2)\)(V). Biểu thức điện áp giữa hai đầu đoạn mạch là
- A u = \(40\cos (100\pi t + \pi /4)\)(V)
- B
u = \(40\sqrt 2 \cos (100\pi t - \pi /4)\)(V) - C
u =\(40\sqrt 2 \cos (100\pi t + \pi /4)\)(V) - D
u =\(40\cos (100\pi t - \pi /4)\)(V)
Đáp án: D
Phương pháp giải:
viết phương trình điện áp
Lời giải chi tiết:
Ta có:
\(R = 10\Omega ,{Z_l} = L.\omega = 10\Omega ,{Z_C} = \frac{1}{{\omega C}} = 20\Omega \)
Cường độ dòng điện hiệu dụng là:
\(I = \frac{{{U_L}}}{{{Z_L}}} = \frac{{20}}{{10}} = 2A\)
Điện trở của mạch là :
\(\begin{gathered}
Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} = 10\sqrt 2 \Omega \hfill \\
U = I.Z = 2.10\sqrt 2 = 20\sqrt 2 V = > {U_0} = 40V \hfill \\
\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R} = - 1 = > \varphi = - \frac{\pi }{4} \hfill \\
= > u = 40\cos (100\pi t - \frac{\pi }{4})V \hfill \\
\end{gathered} \)
Câu hỏi 40 :
Đặt điện áp xoay chiều có giá trị hiệu dụng U =\(30\sqrt 2 \) V vào hai đầu đoạn mạch RLC nối tiếp. Biết cuộn dây thuần cảm, có độ tự cảm L thay đổi được. Khi điện áp hiệu dụng hai đầu cuộn dây đạt cực đại thì hiệu điện thế hai đầu tụ điện là 30V. Giá trị hiệu điện thế hiệu dụng cực đại hai đầu cuộn dây là
- A \(60\sqrt 2 \)V
- B 120V
- C \(30\sqrt 2 \)V
- D 60V
Đáp án: D
Phương pháp giải:
sử dụng giản đồ vecto
Lời giải chi tiết:
Ta có giản đồ vecto sau:
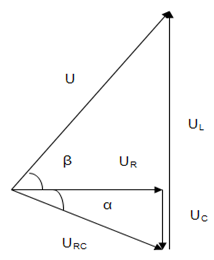
Áp dụng hệ thức lượng trong tam giác ta có:
\(\eqalign{
& {{{U_L}} \over {\sin (\alpha + \beta )}} = {U \over {\sin \gamma }};\sin \gamma = {{{U_R}} \over {{U_{RC}}}} = {R \over {\sqrt {{R^2} + Z_C^2} }} \cr
& {U_{L\max }} \Leftrightarrow \sin (\alpha + \beta ) = 1 \Leftrightarrow \alpha + \beta = {90^0} \Rightarrow {U_{L\max }} = \sqrt {{U^2} + U_{RC}^2} \cr
& {U^2} = U_{L\max }^{}({U_{L\max }} - {U_C}) \Rightarrow {U^2} = U_{L\max }^2 - {U_{L\max }}.{U_C} \Rightarrow {(30\sqrt 2 )^2} = U_{L\max }^2 - {U_{L\max }}.30 \cr
& \Rightarrow \left[ \matrix{
{U_{L1}} = 60V(tm) \hfill \cr
{U_{L2}} = 30V(loai) \hfill \cr} \right. \cr} \)
Vậy UL cực đại là 60V
Câu hỏi 41 :
Cho một nguồn xoay chiều ổn định. Nếu mắc vào nguồn một điện trở thuần R thì dòng điện qua R có giá trị hiệu dụng I1=3A; Nếu mắc tụ Cvào nguồn thì được dòng điệncó cường độ hiệu dụng I2= 4A; Nếu mắc R và C nối tiếp rồi mắc vào nguồn trên thì dòng điện qua mạch có giá trị hiệu dụng là
- A 1A
- B 2,4A
- C 5A
- D 7A
Đáp án: B
Phương pháp giải:
sử dụng định luật Ôm
Lời giải chi tiết:
Áp dụng định luật Ôm tà có:
\(\left\{ \matrix{
{I_1} = {U \over R} = 3A \hfill \cr
{I_2} = {U \over {{Z_C}}} = 4A \hfill \cr} \right. \Rightarrow {R \over {{Z_C}}} = {4 \over 3} \Rightarrow R = {4 \over 3}{Z_C} \Rightarrow {I_3} = {U \over Z} = {U \over {\sqrt {{R^2} + {Z_C}^2} }} = {U \over {{5 \over 3}{Z_C}}} = {4 \over {{5 \over 3}}} = 2,4A\)
Câu hỏi 42 :
Đặt điện áp xoay chiều u = U0cosωt vào hai đầu đoạn mạch AB gồm AM và MB, trong đó AM chứa điện trở thuần R và cuộn dây thuần cảm L, MB chứa tụ điện điện dung C thay đổi được. Điều chỉnh C đến giá trị C0 để điện áp hiệu dụng giữa hai đầu tụ điện đạt giá trị cực đại, khi đó điện áp tức thời giữa A và M có giá trị cực đại là 84,5V. Giữ nguyên giá trị C0 của tụ điện. Ở thời điểm t0, điện áp hai đầu tụ điện; cuộn cảm thuần và điện trở có độ lớn lần lượt là 202,8V ; 30 V và uR. Giá trị uR bằng
- A 50V
- B 60V
- C 30V
- D 40V
Đáp án: C
Phương pháp giải:
áp dụng giản đồ vec to và hệ thức lượng trong tam giác
Lời giải chi tiết:
Ta vẽ giản đồ vec to:
\({U_{0RL}} = {U_{0L}} - {U_{0C}} = 84,5V; - {{{U_L}} \over {{U_C}}} = \left| {{{{u_L}} \over {{u_C}}}} \right| = {{30} \over {202,8}}\)
\({U_{0RL}} = {U_{0L}} - {U_{0C}} = 84,5\)V
\(\Delta OAB \sim \Delta HAO \Rightarrow {U_{0L}}.{O_{0L}} = U_{0RL}^2 \Rightarrow {U_{0C}}.{U_{0L}} = U_{0RL}^2 = {84,5^2}\)
Mà:
\({{{U_{0C}}} \over {{U_{0L}}}} = {{{U_C}} \over {{U_L}}} = {{202,8} \over {30}} = {{169} \over {25}} \Rightarrow {U_{0L}} = 32,5V;{U_{0R}} = 78V \Rightarrow {({{{U_{0L}}} \over {{U_{0L}}}})^2} + {({{{U_R}} \over {{U_{0R}}}})^2} = 1 \Rightarrow {U_R} = 30V\)
Câu hỏi 43 :
Một mạch điện gồm điện trở thuần R, tụ điện C và cuộn cảm thuần L mắc nối tiếp, trong đó độ tự cảm L có thể thay đổi được. Đặt vào mạch điện một điện áp xoay chiều thì điện áp hiệu dụng trên mỗi phần tử lần lượt là UR = 30 V, UC = 60 V, UL = 20V. Giữ nguyên điện áp giữa hai đầu đoạn mạch , thay đổi độ tự cảm L để điện áp hiệu dụng giữa hai đầu cuộn cảm là 40V thì điện áp hiệu dụng giữa hai đầu điện trở R gần nhất với giá trị nào sau đây?
- A 30V
- B 40V
- C 60V
- D 50V
Đáp án: B
Phương pháp giải:
Sử dụng công thức tính điện áp hiệu dụng hai đầu đoạn mạch
Lời giải chi tiết:
Điện áp hiệu dụng giữa hai đầu đoạn mạch :
\(U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}} = \sqrt {{{30}^2} + {{\left( {20 - 60} \right)}^2}} = 50V\)
Ta có: \({{{U_R}} \over {{U_C}}} = {R \over {{Z_C}}} = {{30} \over {60}} = {1 \over 2} \Rightarrow {U_C} = 2{U_R}\)
Khi L thay đổi ta có:
\(\eqalign{
& {U_L}' = 40V;{U_C}' = 2{U_R}' \cr
& \Rightarrow U = \sqrt {{U_R}{'^2} + {{\left( {{U_L}' - {U_C}'} \right)}^2}} \Leftrightarrow 50 = \sqrt {{U_R}{'^2} + {{\left( {40 - 2{U_R}'} \right)}^2}} \cr
& \Leftrightarrow {U_R}{'^2} + {\left( {40 - 2{U_R}'} \right)^2} = {50^2} \Leftrightarrow 5{U_R}{'^2} - 160{U_R}' - 900 = 0 \cr
& \Leftrightarrow {U_R}' = 36,88\Omega \cr} \)
=> Chọn B
Câu hỏi 44 :
Lần lượt mắc điện trở R, cuộn dây thuần cảm có độ tự cảm L, tụ điện có điện dung C vào điện áp xoay chiều \(u = U\sqrt 2 \cos \omega t\left( V \right)\) thì cường độ hiệu dụng có giá trị lần lượt là 4A, 6 A và 2 A. Nếu mắc nối tiếp các phần tử trên vào điện áp \(u = 2U\sqrt 2 \cos \omega t\left( V \right)\) thì cường độ hiệu dụng của dòng điện qua mạch là
- A 4 A
- B 4,8 A
- C 2,4 A
- D 12 A
Đáp án: B
Phương pháp giải:
Sử dụng lí thuyết về định luật Ôm cho đoạn mạch xoay chiều mắc nối tiếp
Lời giải chi tiết:
+ Khi mắc lần lượt các linh kiện vào điện áp xoay chiều \(u = U\sqrt 2 \cos \omega t\left( V \right)\) ta có
\({I_R} = \frac{U}{R} = 4A;{I_L} = \frac{U}{{{Z_L}}} = 6A;{I_C} = \frac{U}{{{Z_C}}} = 2A\)
Suy ra giá trị điện trở, cảm kháng và dung kháng của mạch
\(R = \frac{U}{{{I_R}}} = \frac{U}{4};{Z_L} = \frac{U}{{{I_L}}} = \frac{U}{6};{Z_C} = \frac{U}{{{I_C}}} = \frac{U}{2}\)
+ Khi mắc nối tiếp các linh kiện rồi mắc vào điện áp \(u = 2U\sqrt 2 \cos \omega t\left( V \right)\) thì ta có
\(I = \frac{{2U}}{Z} = \frac{{2U}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{2}{{\sqrt {\frac{1}{{{4^2}}} + {{\left( {\frac{1}{6} - \frac{1}{2}} \right)}^2}} }} = 4,8A\)
Chọn B
Câu hỏi 45 :
Nếu đặt vào hai đầu cuộn dây một hiệu điện thế một chiều 15V thì cường độ dòng điện trong cuộn dây là 0,5A. Nếu đặt vào hai đầu cuộn dây một hiệu điện thế xoay chiều có giá trị hiệu dụng là 15V thì cường độ hiệu dụng của dòng điện qua cuộn dây là 0,3A. Điện trở thuần và cảm kháng của cuộn dây có giá trị là
- A 30Ω ; 50Ω.
- B 30Ω ; 24Ω.
- C 7,5Ω; 50Ω.
- D 30Ω ; 40Ω.
Đáp án: D
Phương pháp giải:
Sử dụng tính chất dẫn điện của cuộn dây có điện trở thuần, lí thuyết về mạch điện xoay chiều chứa cuộn dây
Lời giải chi tiết:
+ Khi đặt hiệu điện thế một chiều 15 V vào hai đầu cuộn dây ta có
\(R = {{{U_1}} \over {{I_1}}} = {{15} \over {0,5}} = 30\Omega \)
+ Khi đặt hiệu điện thế xoay chiều có giá trị hiệu dụng 15 V vào hai đầu cuộn dây ta có
\(Z = \sqrt {{R^2} + Z_L^2} = {{{U_2}} \over {{I_2}}} = {{15} \over {0,3}} = 50\Omega \Rightarrow {Z_L} = 40\Omega \)
Chọn D
Câu hỏi 46 :
Cho đoạn mạch RLC không phân nhánh \(R = 50\Omega ,L = {2 \over \pi },C = {{{{2.10}^{ - 4}}} \over \pi }F\). Đặt giữa hai đầu đoạn mạch một điện áp xoay chiều có giá trị hiệu dụng 200 V và tần số f thay đổi được. Khi điều chỉnh tần số f để cường độ dòng điện hiệu dụng qua mạch là 4 A thì giá trị của f là
- A f = 25 Hz.
- B f = 50 Hz.
- C f = 40 Hz.
- D f = 100 Hz.
Đáp án: A
Lời giải chi tiết:
Đáp án A
+ Cường độ dòng điện hiệu dụng trong mạch
\(I = {U \over Z} \Leftrightarrow 4 = {{200} \over {\sqrt {{{50}^2} + \left( {{2 \over \pi }2\pi f - {1 \over {{{{{2.10}^{ - 4}}} \over \pi }2\pi f}}} \right)} }} = > f = 25Hz\)
Câu hỏi 47 :
Đặt một điện áp xoay chiều u = U0cosωt V vào hai đầu đoạn mạch AB theo thứ tự gồm điện trở R = 90 Ω, cuộn dây không thuần cảm có điện trở r = 10 Ω và tụ điện có điện dung C thay đổi được. M là điểm nối giữa điện trở R và cuộn dây. Khi C = C1 thì điện áp hiệu dụng hai đầu đoạn mạch MB đạt giá trị cực tiểu bằng U1; khi C = C2 = 0,5C1 thì điện áp hiệu dụng trên tụ điện đạt giá trị cực đại bằng U2. Tỉ số bằng \({{{U_2}} \over {{U_1}}}\).
- A \(9\sqrt 2 \)
- B \(\sqrt 2 \)
- C \(10\sqrt 2 \)
- D \(5\sqrt 2 \)
Đáp án: C
Lời giải chi tiết:
Đáp án C
+ Điện áp hiệu dụng hai đầu MB:
\({U_{MB}} = {{U\sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} } \over {\sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = {U \over {\sqrt {1 + {{{R^2} + 2Rr} \over {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}} }}\)
→ Từ phương trình trên, ta thấy rằng, khi ZC1 = ZL thì UMB = UMBmin = U.
+ Khi C = 0,5C1 → ZC2 = 2ZC1 thì UC = UCmax.
\({Z_{C2}} = {{{{\left( {R + r} \right)}^2} + Z_L^2} \over {{Z_L}}} \to {Z_{C1}} = {{{{\left( {90 + 10} \right)}^2} + Z_{C1}^2} \over {{Z_{C1}}}} \to {Z_{C1}} = 100\Omega \to {Z_L} = 100\Omega \)
+ Tỉ số \({{{U_2}} \over {{U_1}}} = {{\sqrt {{{\left( {R + r} \right)}^2} + Z_L^2} } \over {R + r}} = {{\sqrt {{{\left( {90 + 10} \right)}^2} + {{100}^2}} } \over {90 + 10}} = \sqrt 2 \)
Câu hỏi 48 :
Đặt điện áp xoay chiều vào hai đầu đoạn mạch AB như hình vẽ ( tụ điện có C thay đổi được). Điều chỉnh C đến giá trị C0 để điện áp hiệu dụng giữa hai đầu tụ điện đạt giá trị cực đại, khi đó điện áp tức thời giữa A và M có giá trị cực đại là 84,5 V. Giữ nguyên giá trị C0 của tụ điện. Ở thời điểm t0, điện áp hai đầu: tụ điện; cuộn cảm thuần và điện trở có độ lớn lần lượt là 202,8 V; 30 V và uR. Giá trị uR bằng
- A 50 V
- B 60 V.
- C 30 V.
- D 40 V.
Đáp án: C
Phương pháp giải:
Áp dụng giản đồ vecto trong dòng điện xoay chiều
Lời giải chi tiết:
Đáp án C
+ Khi \({U_{\max }}\) thì điện áp hai đầu mạch vuông pha với điện áp hai đầu đoạn mạch RL.
+Áp dụng hệ thức lượng trong tam giác, ta có:\(U_{0RC}^2 = {U_{0L}}{U_{0C\max }}\)
Mặc khác, ta để ý rằng, tại thời điểm t0
\(\left\{ \matrix{
{u_C} = 202,8 \hfill \cr
{u_L} = 30 \hfill \cr} \right.V \to {Z_{C\max }} = {{202,8} \over {30}}{Z_L} \to {U_{0C\max }} = 6,76{U_{0L}}\)
→ Thay vào phương trình hệ thức lượng ta tìm được \({U_{0L}} = 32,5V \to {U_{0R}} = 78\)
Với hai đại lượng vuông pha uL và uR ta luôn có
\({\left( {{{{u_L}} \over {{U_{0L}}}}} \right)^2} + {\left( {{{{u_R}} \over {{U_{0R}}}}} \right)^2} = 1 \leftrightarrow {\left( {{{30} \over {32,5}}} \right)^2} + {\left( {{{{u_R}} \over {78}}} \right)^2} = 1 \to {u_R} = 30V\)
Câu hỏi 49 :
Một đoạn mạch AB gồm các phần tử R, L, C mắc nối tiếp với R = 50 Ω; C thay đổi được. Gọi M là điểm nằm giữa L và C. Đặt điện áp xoay chiều u = U0cos100πt vào hai đầu đoạn mạch AB, U0 không đổi. Điều chỉnh điện dung của tụ điện đến giá trị \(C = {{80} \over \pi }\mu F\) thì điện áp hai đầu đoạn mạch AB lệch pha 900 so với điện áp hai đầu đoạn mạch AM. Giá trị của L có thể bằng
- A \({1 \over {2\pi }}H\)
- B \({2 \over {\pi }}H\)
- C \({1 \over {4 }}H\)
- D \({4 \over {\pi }}H\)
Đáp án: C
Lời giải chi tiết:
Đáp án C.
+ Khi \({\rm{C = }}{{80} \over \pi }\mu {\rm{F}} \to {{\rm{Z}}_{\rm{C}}} = 125\Omega \) thì u vuông pha với \({{\rm{u}}_{{\rm{RL}}}} \to \) điện áp hiệu dụng trên tụ đạt giá trị cực đại
Áp dụng hệ thức lượng trong tam giác \({{\rm{R}}^2} + {\rm{Z}}_{\rm{L}}^2 = {{\rm{Z}}_{\rm{L}}}{{\rm{Z}}_{{\rm{Cmax}}}} \leftrightarrow {\rm{Z}}_{{\rm{Lmax}}}^2 - 125{{\rm{Z}}_{\rm{L}}} + 2500 = 0.\)
+ Phương trình trên ta có nghiệm \({{\rm{Z}}_{{\rm{L1}}}} = 100\Omega \to {\rm{L = }}{1 \over \pi }{\rm{H,}}\) hoặc \({{\rm{Z}}_{{\rm{L2}}}} = 25\Omega \to {\rm{L = }}{1 \over {4\pi }}{\rm{H}}{\rm{.}}\)
Câu hỏi 50 :
Đặt một nguồn điện xoay chiều có hiệu điện thế hiệu dụng U và tần số f vào hai đầu của đoạn mạch R, L, C mắc nối tiếp, cuộn dây thuần cảm. Nối hai đầu tụ với một ampe kế thì thấy nó chỉ 1A đồng thời dòng điện chạy qua ampe kế chậm pha π/6 so với hiệu điện thế tức thời giữa hai đầu đoạn mạch. Nếu thay ampe kế bằng một vôn kế thì thấy nó chỉ 195,19V, đồng thời hiệu điện thế tức thời giữa hai đầu vôn kế lệch pha một góc π/4 so với hiệu điện thế tức thời giữa hai đầu đoạn mạch. Hiệu điện thế dụng của nguồn xoay chiều là
- A 125V.
- B 175V.
- C 150V.
- D 100V.
Đáp án: B
Phương pháp giải:
sử dụng định luật Ôm cho đoạn mạch RLC mắc nối tiếp
Lời giải chi tiết:
Ban đầu mạch RLC nối tiếp nhưng dùng Ampe kế nối tắt qua tụ nên đoạn mạch chỉ còn còn RL. Do I trễ pha so với u một góc \(\frac{\pi }{6}\)
nên ta có:
\(\tan \frac{\pi }{6} = \frac{{{Z_L}}}{R} = \frac{1}{{\sqrt 3 }} = > R = \sqrt 3 {Z_L}\)
Khi thay thế ampe kế bằng vôn kế thì vôn kế đo giá trị hiệu điện thế hiệu dụng trên tụ C. mạch RLC nối tiếp và điện áp tức thời trên tụ trễ pha
\(\frac{\pi }{4}\) so với điện áp trên đoạn mạch. Ta có giản đồ vecto:
ta có
\(\begin{gathered}
\tan \frac{{ - \pi }}{4} = \frac{{{Z_L} - {Z_C}}}{R} = - 1 \hfill \\
= > {Z_C} - Z{}_L = R \hfill \\
= > {Z_C} = R + {Z_L} = \left( {1 + \frac{1}{{\sqrt 3 }}} \right)R \hfill \\
\end{gathered} \)
mà
\(\begin{gathered}
{U_{AB}} = I.Z = I.\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = I.\sqrt 2 .R \hfill \\
{U_C} = I.{Z_C} = I.(\frac{1}{{\sqrt 3 }} + 1).R \hfill \\
\end{gathered} \)
Lập tỉ số
\(\frac{{{U_{AB}}}}{{{U_C}}} = \frac{{\sqrt 2 }}{{\frac{1}{{\sqrt 3 }} + 1}} = > {U_{AB}} = \frac{{\sqrt 2 }}{{\frac{1}{{\sqrt 3 }} + 1}}{U_C} = \frac{{\sqrt 2 }}{{\frac{1}{{\sqrt 3 }} + 1}}.195,19 = 175V\)