Câu hỏi 1 :
Cường độ dòng điện xoay chiều trong một đoạn mạch là i = 4\(\sqrt{2}\) cos(100πt + π/3)(A) (t tính bằng s) cường độ dòng điện hiệu dụng của đoạn mạch là:
- A 2A
- B 4A
- C 4\(\sqrt{2}\)A
- D 8A
Đáp án: B
Phương pháp giải:
Biểu thức liên hệ giữa cường độ dòng điện cực đại và hiệu dụng: \({{I}_{0}}=I\sqrt{2}\)
Lời giải chi tiết:
Vì \({{I}_{0}}=I\sqrt{2}=4\sqrt{2}A\) nên I = 4A
Câu hỏi 2 :
Một dòng điện xoay chiều có biểu thức i = 4cos(100πt + π/3) (A). Chọn phát biểu đúng?
- A I = 4A
- B T = 0,01s
- C f = 100Hz
- D Io = 4A
Đáp án: D
Phương pháp giải:
đại cương dòng điện xoay chiều
Lời giải chi tiết:
Io = 4A
Câu hỏi 3 :
Cho dòng điện xoay chiều i = 2cos(100πt + π/2) chạy qua một ampe kế. Số chỉ của ampe kế này là
- A 1A
- B 2A
- C \(2\sqrt{2}A\)
- D \(\sqrt{2}A\)
Đáp án: D
Phương pháp giải:
Số chỉ của ampe kế xoay chiều là cường độ dòng điện hiệu dụng qua mạch.
Liên hệ giữa giá trị cực đại và giá trị hiệu dụng: \(I=\frac{{{I}_{0}}}{\sqrt{2}}\)
Lời giải chi tiết:
I0 = 2A
Cường độ dòng điện hiệu dụng: \(I=\frac{{{I}_{0}}}{\sqrt{2}}=\sqrt{2}A\)
Số chỉ của ampe kế xoay chiều chỉ dòng điện hiệu dụng \(\sqrt{2}A\)
Câu hỏi 4 :
Mắc ampe kế nhiệt xoay chiều nối tiếp với một đoạn mạch thì thấy ampe kế chỉ 1 A. Cường độ dòng điện cực đại của đoạn mạch này là
- A 2 A.
- B \(2\sqrt{2}A\)
- C \(\sqrt{2}A\)
- D 1 A.
Đáp án: C
Phương pháp giải:
Số chỉ am pe kế là dòng điện hiệu dụng
Liên hệ giữa giá trị hiệu dụng và giá trị cực đại: \({{I}_{0}}=I\sqrt{2}\)
Lời giải chi tiết:
Cường độ dòng điện hiệu dụng I = 1A
Cường độ dòng điện cực đại: \({{I}_{0}}=I\sqrt{2}=\sqrt{2}A\)
Câu hỏi 5 :
Dùng ampe kế đo cường độ dòng điện xoay chiều qua điện trở 30Ω thì ampe kế chỉ 2A . Biên độ của hiệu điện thế giữa hai đầu điện trở này bằng
- A 60 V.
- B \(60\sqrt{2}V\)
- C \(30\sqrt{2}V\)
- D \(30V\)
Đáp án: B
Phương pháp giải:
Áp dụng định luật Ôm U = IR
Liên hệ giữa giá trị cực đại và giá trị hiệu dụng: \(I=\frac{{{I}_{0}}}{\sqrt{2}}\)
Lời giải chi tiết:
I = 2A
Biên độ của hiệu điện hế giữa hai đầu điện trở: U0 = I0R = \(60\sqrt{2}V\)
Câu hỏi 6 :
Biểu thức cường độ dòng điện là i = 4cos(100πt + π/4) A. Tại thời điểm t = 0,04s cường độ dòng điện có giá trị là
- A 2A
- B 4A
- C \(2\sqrt{2}A\)
- D \(\sqrt{2}A\)
Đáp án: C
Phương pháp giải:
Cường độ dòng điện tại thời điểm t là \(i=4\cos \left( 100\pi t+\frac{\pi }{4} \right)A\)
Lời giải chi tiết:
Cường độ dòng điện tại thời điểm t = 0,04s là
\(i=4\cos \left( 100\pi t+\frac{\pi }{4} \right)A=4\cos \left( 100\pi .0,04+\frac{\pi }{4} \right)=2\sqrt{2}A\)
Chọn C
Câu hỏi 7 :
Cường độ dòng điện trong mạch có dạng i = \(2\sqrt{2}\) cos120πt (A). Nếu dùng ampe kế nhiệt đo cường độ dòng điện của mạch trên thì ampe kế chỉ bao nhiêu?
- A 4A
- B 2\(\sqrt{2}\)A
- C 2A
- D \(\sqrt{2}\)A
Đáp án: C
Phương pháp giải:
Số chỉ ampe kế nhiệt là cường độ dòng điện hiệu dụng
Liên hệ giữa giá trị hiệu dụng và cực đại: \(I=\frac{{{I}_{0}}}{\sqrt{2}}\)
Lời giải chi tiết:
Số chỉ ampe kế nhiệt là cường độ dòng điện hiệu dụng
\(I=\frac{{{I}_{0}}}{\sqrt{2}}=2A\)
Chọn C
Câu hỏi 8 :
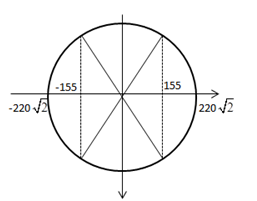
Một đèn neon đặt dưới hiệu điện thế xoay chiều 220V – 50Hz. Biết đèn sáng khi hiệu điện thế giữa hai cực không nhỏ hơn 155V. Tỉ số giữa thời gian đèn sáng và thời gian đèn tắt trong một chu kỳ là
- A 1
- B 0,5
- C 2
- D 3
Đáp án: C
Phương pháp giải:
Liên hệ giữa điện áp cực đại và điện áp hiệu dụng: \({{U}_{0}}=U\sqrt{2}\)
Thời gian đèn sáng ứng với thời gian |u |≥ 155V
Thời gian đèn tắt ứng với thời gian |u| < 155V
Chu kỳ T = 1/f
Lời giải chi tiết:
Chu kỳ dòng điện T = 1/f = 0,02s
Điện áp cực đại: \({{U}_{0}}=U\sqrt{2}=220\sqrt{2}V\)
Ta có u = 155V = U0/2
=> Thời gian đèn sáng trong 1 chu kỳ là : \({{t}_{s}}=\frac{4T}{6}=\frac{2T}{3}\)
Thời gian đèn tắt trong 1 chu kỳ là:
\({{t}_{t}}=T-{{t}_{s}}=T-\frac{2T}{3}=\frac{T}{3}\Rightarrow \frac{{{t}_{s}}}{{{t}_{t}}}=2\)
Chọn C
Câu hỏi 9 :
Từ thông gửi qua một khung dây dẫn phẳng bằng kim loại có biểu thức \(\phi =\frac{2}{\pi }\text{cos}\left( 100\pi t+\frac{\pi }{6} \right)(\text{W}b)\) (t tính bằng giây). Suất điện động cảm ứng xuất hiện trong khung dây là
- A E = -200cos(100πt + π/6) (V)
- B E = -200sin(100πt + π/6) (V)
- C E = 200sin(100πt + π/6) (V)
- D E = 200cos(100πt + π/6) (V)
Đáp án: C
Phương pháp giải:
Suất điện động cảm ứng xuất hiện khi từ thông qua khung dây biến thiên: e = - Ф’
Lời giải chi tiết:
Suất điện động cảm ứng xuất hiện trong khung dây:
\(e=-\phi '=\frac{2}{\pi }.100\pi \sin \left( 100\pi t+\frac{\pi }{6} \right)V=200\sin \left( 100\pi t+\frac{\pi }{6} \right)V\)
Chọn C
Câu hỏi 10 :
Tại thời điểm t, điện áp \(u=200\sqrt{2}\text{cos(100}\pi \text{t-}\frac{\pi }{2})\) (trong đó u tính bằng V, t tính bằng s) có giá trị bằng \(100\sqrt{2}V\) và đang giảm. Sau thời điểm đó 1/300 (s) điện áp này có giá trị
- A -100V
- B 200V
- C \(-100\sqrt{2}V\)
- D \(100\sqrt{3}V\)
Đáp án: C
Phương pháp giải:
Chu kỳ dao động: \(T=\frac{2\pi }{\omega }\)
Lời giải chi tiết:
Điện áp có U0 = \(200\sqrt{2}V\) và pha ban đầu – π/2
Thời điểm có u = \(100\sqrt{2}V\) và đang giảm ứng với vị trí góc π/3
Chu kỳ \(T=\frac{2\pi }{\omega }=0,02s\)
Sau đó 1/300s = T/6 ứng với vị trí góc 2π/3 nên điện áp có giá trị - \(100\sqrt{2}V\)
Chọn C
Câu hỏi 11 :
Cho điện áp hai đầu tụ có điện dung \(C = \frac{{{{10}^{ - 4}}}}{\pi }F\) là \(u = 100\cos \left( {100\pi t - \frac{\pi }{2}} \right)V\). Biểu thức dòng điện qua mạch là
- A \(i = \cos \left( {100\pi t} \right)(A)\)
- B \(i = 4\cos \left( {100\pi t} \right)(A)\)
- C \(i = \cos \left( {100\pi t - \pi } \right)(A)\)
- D \(i = 4\cos \left( {100\pi t - \frac{\pi }{2}} \right)(A)\)
Đáp án: A
Phương pháp giải:
Phương pháp:
Trong mạch điện xoay chiều chỉ chứa tụ điện , điện áp trễ pha hơn cường độ dòng điện là \(\frac{\pi }{2}\)
Lời giải chi tiết:
Cách giải:
Cường độ dòng điện trong mạch có giá trị là \(i = \frac{{{U_0}}}{{{Z_C}}}\cos \left( {100\pi t} \right)(A) = {U_0}.\omega C\cos \left( {100\pi t} \right)(A) = 100.100\pi .\frac{{{{10}^{ - 4}}}}{\pi }\cos \left( {100\pi t} \right)(A) = \cos \left( {100\pi t} \right)(A)\)
Chọn A
Câu hỏi 12 :
Biểu thức cường độ dòng điện là \(i = 4.\cos \left( {100\pi t - \frac{\pi }{4}} \right)A\). Tại thời điểm t = 10,18s cường độ dòng điện có giá trị là :
- A i = 0A
- B i = 2A
- C i = 4A
- D \(i = 2\sqrt 2 A\)
Đáp án: D
Phương pháp giải:
Phương pháp:
Thay t vào phương trình của i
Lời giải chi tiết:
Cách giải:
Ta có: \(i = 4.\cos \left( {100\pi .20,18 - \frac{\pi }{4}} \right) = 2\sqrt 2 A\)
Chọn D
Câu hỏi 13 :
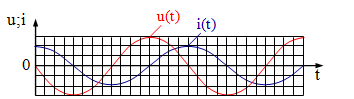
Trong hình là đồ thị biểu diễn sự biến đổi của điện áp giữa hai đầu một đoạn mạch xoay chiều và cường độ dòng điện chạy trong đoạn mạch đó theo thời gian. Kết luận nào sau đây là đúng khi nói về độ lệch pha giữa u(t) và i(t)?
- A u(t) nhanh pha so với i(t) một góc \(\frac{{{\rm{2}}\pi }}{{\rm{3}}}\) rad.
- B u(t) nhanh pha so với i(t) một góc \(\frac{\pi }{{\rm{2}}}\) rad.
- C u(t) chậm pha so với i(t) một góc \(\frac{{{\rm{2}}\pi }}{{\rm{3}}}\) rad.
- D u(t) chậm pha so với i(t) một góc \(\frac{\pi }{{\rm{2}}}\) rad.
Đáp án: B
Lời giải chi tiết:
Cách giải:
Từ đồ thị ta thấy, lúc t = 0 thì
\(\left\{ \begin{array}{l}i = {I_0} = > {\varphi _i} = 0\\\left\{ \begin{array}{l}u = 0\\u{'_t} < 0\end{array} \right.\end{array} \right. = > {\varphi _u} = \frac{\pi }{2}\)
Chọn B
Câu hỏi 14 :
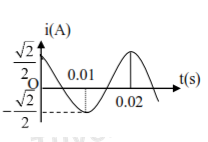
Dòng điện xoay chiều chạy qua một đoạn mạch có cường độ biến đổi điều hoà theo thời gian được mô tả bằng đồ thị ở hình bên. Biểu thức cường độ dòng điện tức thời của đoạn mạch đó là
- A \(i = 4\cos \left( {100\pi t + \frac{{\pi {\rm{\;}}}}{4}} \right){\mkern 1mu} A\)
- B \(i = 4\cos \left( {120\pi t - \frac{{\pi {\rm{\;}}}}{4}} \right){\mkern 1mu} A\)
- C \(i = 4\cos \left( {100\pi t - \frac{{\pi {\rm{\;}}}}{4}} \right){\mkern 1mu} A\)
- D \(i = 4\cos \left( {120\pi t + \frac{{\pi {\rm{\;}}}}{4}} \right)A\)
Đáp án: C
Lời giải chi tiết:
Cách giải:
+ Từ đồ thị, ta có \({I_0} = 4{\rm{A}}\), tại t =0 ,\(i = \frac{{\sqrt 2 }}{2}{I_0}\) và đang tăng \( \to {\varphi _0} = {\rm{\;}} - \frac{{\pi {\rm{\;}}}}{4}.\)
Từ thời điểm t = 0 đến thời điểm \(t = 0,{25.10^{ - 2}}s\) ứng với \(\Delta t = \frac{T}{8} \to T = 0,02{\rm{s}} \to \omega {\rm{\;}} = 100\pi rad/s.\) \( \to i = 4\cos \left( {100\pi t - \frac{{\pi {\rm{\;}}}}{4}} \right)A.\)
Chọn C
Câu hỏi 15 :
Cho dòng điện xoay chiều có biểu thức \(i=4\sqrt{2}\cos \left( 100\pi t+\frac{\pi }{3} \right)\,(A)\). Cường độ dòng điện hiệu dụng có giá trị bằng
- A 4 A.
- B \(4\sqrt{2}\)A.
- C \(2\sqrt{2}\)A.
- D 2 A.
Đáp án: A
Phương pháp giải:
Áp dụng công thức tính cường độ dòng điện hiệu dụng: \(I=\frac{{{I}_{o}}}{\sqrt{2}}\)
Lời giải chi tiết:
Cường độ dòng điện hiệu dụng: \(I=\frac{{{I}_{o}}}{\sqrt{2}}=\frac{4\sqrt{2}}{\sqrt{2}}=4\)(A)
Chọn A
Câu hỏi 16 :
Tại thời điểm t, điện áp \(u = 200\sqrt 2 {\rm{cos(100}}\pi {\rm{t - }}\frac{\pi }{2})\) (trong đó u tính bằng V, t tính bằng s) có giá trị bằng \(100\sqrt 2 V\) và đang giảm. Sau thời điểm đó 1/300 (s) điện áp này có giá trị
- A -100V
- B 200V
- C \( - 100\sqrt 2 V\)
- D \(100\sqrt 3 V\)
Đáp án: C
Phương pháp giải:
Phương pháp:
Chu kỳ dao động: \(T = \frac{{2\pi }}{\omega }\)
Lời giải chi tiết:
Cách giải:
Điện áp có U0 = \(200\sqrt 2 V\) và pha ban đầu – π/2
Thời điểm có u = \(100\sqrt 2 V\) và đang giảm ứng với vị trí góc π/3
Chu kỳ \(T = \frac{{2\pi }}{\omega } = 0,02s\)
Sau đó 1/300s = T/6 ứng với vị trí góc 2π/3 nên điện áp có giá trị - \(100\sqrt 2 V\)
Chọn C
Câu hỏi 17 :
Từ thông qua một vòng dây dẫn có biểu thức \(\Phi \text{ }=\text{ }{{\Phi }_{0}}cos(\omega t-\text{ }\pi /6)\)thì suất điện động cảm ứng xuất hiện trong vòng dây đó có biểu thức \(e={{E}_{0}}cos(\omega t\text{ }+\text{ }\varphi \text{ }\text{ }\pi /12)\)(với \(\omega ,\text{ }{{E}_{0}},\text{ }{{\Phi }_{0}}\)là các hằng số dương). Giá trị của φ là
- A \(-\frac{7\pi }{12}\) rad
- B \(-\frac{\pi }{12}\)rad.
- C \(\frac{\pi }{3}\)rad
- D \(\frac{5\pi }{12}\)rad
Đáp án: A
Phương pháp giải:
Từ thông nhanh pha π/2 so với suất điện động
Lời giải chi tiết:
Từ thông nhanh pha π/2 so với suất điện động: \({{\varphi }_{\Phi }}-{{\varphi }_{e}}=\frac{\pi }{2}\to -\frac{\pi }{6}-(\varphi -\frac{\pi }{12})=\frac{\pi }{2}\Rightarrow \varphi =\frac{-7\pi }{12}\)
Chọn A
Câu hỏi 18 :
Cho biểu thức của cường độ dòng điện xoay chiều là \(i = \;2{I_0}cos(\omega t + \varphi )A\) . Cường độ hiệu dụng của dòng điện xoay chiều đó là
- A I = 2I0
- B I =\(\sqrt 2 \)I0
- C I =\(\frac{{{I_0}}}{2}\)
- D I=\(\frac{{{I_0}}}{{\sqrt 2 }}\)
Đáp án: B
Phương pháp giải:
Cường độ hiệu dụng
\(I = \frac{{{I_{cd}}}}{{\sqrt 2 }}\)
Lời giải chi tiết:
Cường độ hiệu dụng
\(I = \frac{{{I_{c{\rm{d}}}}}}{{\sqrt 2 }} = \frac{{2{I_0}}}{{\sqrt 2 }} = \sqrt 2 {I_0}\)
Câu hỏi 19 :
Cường độ dòng điện tức thời chạy qua một đoạn mạch điện xoay chiều là i = 4cos(20πt) (A), t đo bằng giây. Tại thời điểm t1 nào đó dòng điện đang giảm và có cường độ bằng i1 = - 2A. Hỏi đến thời điểm t2 = t1 + 0,025s cường độ dòng điện tức thời là:
- A \(2\sqrt 3 A\)
- B \( - 2\sqrt 3 A\)
- C 2A
- D -2A
Đáp án: B
Phương pháp giải:
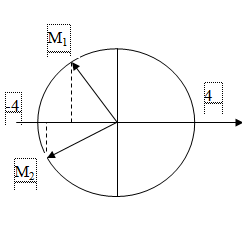
Sử dụng giản đồ vecto quay.
Chu kì: \(T = \frac{{2\pi }}{\omega } = 0,1s \Rightarrow 0,025s = \frac{T}{4}\)
Ứng với góc quay 900
Lời giải chi tiết:
Chu kì: \(T = \frac{{2\pi }}{\omega } = 0,1s \Rightarrow 0,025s = \frac{T}{4}\)
Ứng với góc quay 900 của vecto quay.
Sử dụng phương pháp vecto quay ta có hình vẽ:
Từ hình xác định vị trí ứng với M2, ta có: \({i_2} = - 2\sqrt 3 A\)
Chọn B
Câu hỏi 20 :
Một dòng điện xoay chiều có cường độ \({\rm{i = 2}}\sqrt[]{2}{\rm{cos}}\left( {{\rm{100}}\pi {\rm{t + }}\dfrac{\pi }{2}} \right){\rm{(A) }}\)Chọn phát biểu sai:
- A Cường độ hiệu dụng I = 2A
- B f = 50Hz.
- C Tại thời điểm t = 0,15s cường độ dòng điện cực đại
- D \(\varphi \,{\rm{ = }}\dfrac{\pi }{2}{\rm{ }}\)
Đáp án: C
Phương pháp giải:
Cường độ dòng điện hiệu dụng: \(I = \dfrac{{{I_0}}}{{\sqrt 2 }}\)
Tần số: \(f = \dfrac{\omega }{{2\pi }}\)
Thay t vào biểu thức của i xác định được giá trị của i tại thời điểm t
Lời giải chi tiết:
Từ biểu thức của cường độ dòng điện ta có: \(\left\{ \begin{array}{l}I = \dfrac{{{I_0}}}{{\sqrt 2 }} = \dfrac{{2\sqrt 2 }}{{\sqrt 2 }} = 2A\\f = \dfrac{\omega }{{2\pi }} = \dfrac{{100\pi }}{{2\pi }} = 50Hz\\{\varphi _i} = \dfrac{\pi }{2}\end{array} \right.\)
Tại thời điểm t = 0,15s ta có: \({\rm{i = 2}}\sqrt[]{2}{\rm{cos}}\left( {{\rm{100}}\pi .0,15{\rm{ + }}\dfrac{\pi }{2}} \right) = 0\)
Vậy phát biểu sai: Tại thời điểm t = 0,15s cường độ dòng điện cực đại
Chọn C.
Câu hỏi 21 :
Một dòng điện xoay chiều có phương trình \(i = 2\cos (2\pi f.t)\,\,\left( A \right)\). Biết rằng trong 1s đầu tiên dòng điện đổi chiều 119 lần, hãy xác định tần số của dòng điện?
- A 60Hz
- B 50Hz
- C 59,5Hz
- D 119Hz
Đáp án: A
Phương pháp giải:
Nếu phương trình của cường độ dòng điện là \(i = {I_0}.\cos \left( {\omega t + k2\pi } \right)\) thì trong 1s đầu tiên dòng điện đổi chiều: \(N = 2f - 1\) (lần)
Lời giải chi tiết:
Phương trình của cường độ dòng điện: \(i = 2\cos (2\pi f.t)\,\,\left( A \right)\)
Trong 1 giây đầu tiên dòng điện đổi chiều 119 lần, ta có:
\(N = 2f - 1 = 119 \Rightarrow f = 60Hz\)
Chọn A.
Câu hỏi 22 :
Biểu thức dòng điện trong mạch có dạng \(i = 4.\cos \left( {8\pi t + \dfrac{\pi }{6}} \right)A\), vào thời điểm t dòng điện bằng 0,7A. Hỏi sau 3s dòng điện có giá trị là bao nhiêu?
- A - 0,7A
- B 0,7A
- C 0,5A
- D 0,75A
Đáp án: B
Phương pháp giải:
Thay t vào phương trình của i
Công thức lượng giác: \(\cos \left( {\alpha + k2\pi } \right) = \cos \alpha \)
Lời giải chi tiết:
Thay t vào biểu thức của cường độ dòng điện i ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}i\left( t \right) = 4.\cos \left( {8\pi t + \dfrac{\pi }{6}} \right) = 0,7A\\i\left( {t + 3} \right) = 4.\cos \left[ {8\pi \left( {t + 3} \right) + \dfrac{\pi }{6}} \right] = 4.\cos \left( {8\pi t + \dfrac{\pi }{6} + 24\pi } \right)A\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}i\left( t \right) = 4.\cos \left( {8\pi t + \dfrac{\pi }{6}} \right) = 0,7A\\i\left( {t + 3} \right) = 4.\cos \left( {8\pi t + \dfrac{\pi }{6} + 24\pi } \right) = 4.\cos \left( {8\pi t + \dfrac{\pi }{6}} \right)\end{array} \right.\\ \Rightarrow i\left( {t + 3} \right) = i\left( t \right) = 0,7A\end{array}\)
Chọn B.
Câu hỏi 23 :
Cho dòng điện có biểu thức \(i = 2\cos \left( {100\pi t - \dfrac{\pi }{3}} \right){\rm{ }}A\). Những thời điểm nào tại đó cường độ tức thời có độ lớn đạt giá trị cực tiểu?
- A \(t = - \dfrac{5}{{600}} + \dfrac{k}{{100}}s;\left( {k = 1,2,..} \right)\)
- B \(t = \dfrac{5}{{600}} + \dfrac{k}{{100}}s;\left( {k = 0,1,2,..} \right)\)
- C \(t = \dfrac{1}{{120}} + \dfrac{k}{{100}}s;\left( {k = 1,2,..} \right)\)
- D \(t = - \dfrac{1}{{120}} + \dfrac{k}{{100}}s;\left( {k = 1,2,..} \right)\)
Đáp án: B
Phương pháp giải:
Giải phương trình lượng giác: \(\cos \alpha = 0 \Leftrightarrow \alpha = \dfrac{\pi }{2} + k\pi \)
Lời giải chi tiết:
Cường độ dòng điện có độ lớn cực tiểu:
\(\begin{array}{l}\left| i \right| = 0 \Leftrightarrow 2\cos \left( {100\pi t - \dfrac{\pi }{3}} \right) = 0\\ \Leftrightarrow \cos \left( {100\pi t - \dfrac{\pi }{3}} \right) = 0 \Leftrightarrow 100\pi t - \dfrac{\pi }{3} = \dfrac{\pi }{2} + k\pi \\ \Leftrightarrow t = \dfrac{5}{{600}} + \dfrac{k}{{100}}s;k = 0;1;2;...\end{array}\)
Chọn B.
Câu hỏi 24 :
Dòng điện xoay chiều có cường độ \(i = 2\cos (100\pi t)\left( A \right)\)chạy qua một đoạn mạch điện. Số lần dòng điện có độ lớn 1(A) trong 1(s) là:
- A 200 lần
- B 400 lần
- C 100 lần
- D 50 lần
Đáp án: A
Phương pháp giải:
Trong 1 chu kì có 4 lần dòng đện có độ lớn 1A
Phân tích: \(\Delta t = n.T;n \in N\)
Trong n chu kì có 4n (lần) dòng điện có độ lớn 1A
Lời giải chi tiết:
Chu kì: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{100\pi }} = 0,02s\)
Ta có: \(1s = 50.0,02 = 50.T\)
Trong 1 chu kì có 4 lần dòng điện có độ lớn 1A
Vậy trong 50T sẽ có số lần dòng điện có độ lớn 1A là:
\(N = 50.4 = 200\) (lần)
Chọn A.
Câu hỏi 25 :
Dòng điện xoay chiều \(i = 2.\sin 100\pi t\left( A \right)\)qua một dây dẫn. Điện lượng chạy qua tiết diện dây trong khoảng thời gian từ 0 đến 0,15s là :
- A 0
- B \(\dfrac{4}{{100\pi }}\left( C \right)\)
- C \(\dfrac{3}{{100\pi }}\left( C \right)\)
- D \(\dfrac{6}{{100\pi }}\left( C \right)\)
Đáp án: B
Phương pháp giải:
Điện lượng qua tiết diện S trong thời gian từ t1 đến t2 là Δq : \(q = \int\limits_{{t_1}}^{{t_2}} {i.dt} \)
Lời giải chi tiết:
Điện lượng chạy qua tiết diện dây trong khoảng thời gian từ 0 đến 0,15s là :
\(q = \int\limits_{{t_1}}^{{t_2}} {i.dt} \int\limits_0^{0,15} {2.\sin 100\pi t} .dt = - \dfrac{{2.\cos 100\pi t}}{{100\pi }}\left| {_0^{0,15}} \right. = \dfrac{4}{{100\pi }}\left( C \right)\)
Chọn B.
Câu hỏi 26 :
Biểu thức của điện áp xoay chiều là: \(u = 220\sqrt 2 .\cos \left( {100\pi t} \right)\,\left( V \right)\). Khoảng thời gian ngắn nhất u = 0 đến khi \(u = 110\sqrt 2 V\) là:
- A \(\dfrac{1}{{200}}s\)
- B \(\dfrac{1}{{300}}s\)
- C \(\dfrac{1}{{600}}s\)
- D \(\dfrac{1}{{400}}s\)
Đáp án: C
Phương pháp giải:
Sử dụng VTLG và công thức tính thời gian: \(\Delta t = \dfrac{\alpha }{\omega } = \alpha .\dfrac{T}{{2\pi }}\)
Lời giải chi tiết:
Biểu diễn trên VTLG ta có:
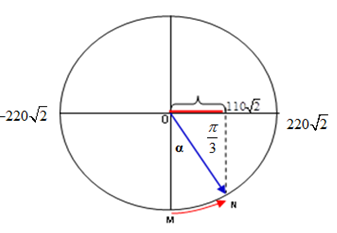
Góc quét được là: \(\alpha = \dfrac{\pi }{2} - \dfrac{\pi }{3} = \dfrac{\pi }{6}rad\)
Khoảng thời gian ngắn nhất u = 0 đến khi \(u = 110\sqrt 2 V\) là:
\(\Delta t = \dfrac{\alpha }{\omega } = \dfrac{{\dfrac{\pi }{6}}}{{100\pi }} = \dfrac{1}{{600}}s\)
Chọn C.
Câu hỏi 27 :
Từ thông qua một vòng dây dẫn là \(\Phi = \dfrac{{{{2.10}^{ - 2}}}}{\pi }\cos \left( {100\pi t + \dfrac{\pi }{4}} \right)\left( {Wb} \right)\). Biểu thức của suất điện động cảm ứng xuất hiện trong vòng dây này là:
- A \(e = 2\cos \left( {100\pi t + \dfrac{\pi }{4}} \right)\left( V \right)\)
- B \(e = 2\cos \left( {100\pi t - \dfrac{\pi }{4}} \right)\left( V \right)\)
- C \(e = 2\cos \left( {100\pi t} \right)\left( V \right)\)
- D \(e = 2\cos \left( {100\pi t + \dfrac{\pi }{2}} \right)\left( V \right)\)
Đáp án: B
Phương pháp giải:
Từ thông qua khung dây:
\(\Phi = NBS.\cos \left( {\overrightarrow n ;\overrightarrow B } \right) = NBS.\cos \left( {\omega t + \varphi } \right) = {\Phi _0}\cos \left( {\omega t + \varphi } \right)\)
Suất động trong khung dây:
\(e = - \dfrac{{d\Phi }}{{dt}} = - \Phi ' = \omega NBS.\sin \left( {\omega t + \varphi } \right) = \omega NBS.\cos \left( {\omega t + \varphi - \dfrac{\pi }{2}} \right) = {E_0}.\cos \left( {\omega t + \varphi - \dfrac{\pi }{2}} \right)\)
Lời giải chi tiết:
Phương trình của từ thông: \(\Phi = \dfrac{{{{2.10}^{ - 2}}}}{\pi }\cos \left( {100\pi t + \dfrac{\pi }{4}} \right)\left( {Wb} \right)\)
Biểu thức của suất điện động cảm ứng:
\(e = - \Phi ' = 100\pi .\dfrac{{{{2.10}^{ - 2}}}}{\pi }\cos \left( {100\pi t + \dfrac{\pi }{4} - \dfrac{\pi }{2}} \right) = 2.\cos \left( {100\pi t - \dfrac{\pi }{4}} \right)V\)
Chọn B.
Câu hỏi 28 :
Dòng điện có cường độ \(i = 2\sqrt 2 .\cos 100\pi t\,\,\left( A \right)\)chạy qua điện trở thuần 100Ω. Trong 30 giây, nhiệt lượng tỏa ra trên điện trở là
- A 12 kJ
- B 24 kJ
- C 4243J
- D 8485J
Đáp án: A
Phương pháp giải:
Nhiệt lượng toả ra trên điện trở: \(Q = {I^2}Rt\)
Lời giải chi tiết:
Nhiệt lượng toả ra trên điện trở trong 30s là:
\(Q = {I^2}Rt = {2^2}.100.30 = 12000J = 12kJ\)
Chọn A.
Câu hỏi 29 :
Một khung dây phẳng diện tích 10 cm2 đặt trong từ trường đều có vectơ cảm ứng vuông góc với mặt phẳng khung dây và có độ lớn 0,08 T. Từ thông qua khung dây này là
- A 8.10-7 Wb.
- B 8.10-3 Wb.
- C 0.
- D 8.10-5 Wb.
Đáp án: D
Phương pháp giải:
Công thức tính từ thông: \(\Phi = B.S.\cos \alpha \)
Trong đó: α là góc giữa vecto cảm ứng từ và pháp tuyến.
Lời giải chi tiết:
Từ thông qua khung dây này là:
\(\Phi = B.S.\cos \alpha = {10.10^{ - 4}}.0,08.cos0 = {8.10^{ - 5}}{\rm{W}}b\)
Chọn D.
Câu hỏi 30 :
Cho suất điện động \(e = 15\cos \left( {4\pi t + \dfrac{\pi }{3}} \right)\,\,\left( V \right)\). Tại thời điểm \(t = 10\,\,s\), độ lớn suất điện động là
- A \(7,5\,\,V\).
- B \(7\,\,V\).
- C \(4\,\,V\).
- D \(5\,\,V\).
Đáp án: A
Phương pháp giải:
Thay thời gian vào phương trình suất điện động
Lời giải chi tiết:
Suất điện động tại thời điểm \(t = 10\,\,s\) là:
\(e = 15\cos \left( {4\pi .10 + \dfrac{\pi }{3}} \right) = 7,5\,\,\left( V \right)\)
Chọn A.
Câu hỏi 31 :
Dòng điện chạy qua một đoạn mạch có biểu thức \(i = {I_0}\sin 100\pi t\). Trong khoảng thời gian từ \(0\) đến \(0,01\,\,s\), cường độ dòng điện tức thời có giá trị bằng \(0,5{I_0}\) vào những thời điểm
- A \(\dfrac{1}{{600}}\,\,s\) và \(\dfrac{5}{{600}}\,\,s\).
- B \(\dfrac{1}{{500}}\,\,s\) và \(\dfrac{3}{{500}}\,\,s\).
- C \(\dfrac{1}{{300}}\,\,s\) và \(\dfrac{2}{{300}}\,\,s\).
- D \(\dfrac{1}{{400}}\,\,s\) và \(\dfrac{2}{{400}}\,\,s\).
Đáp án: A
Phương pháp giải:
Chu kì của dòng điện: \(T = \dfrac{{2\pi }}{\omega }\)
Sử dụng vòng tròn lượng giác và công thức: \(t = \dfrac{\varphi }{\omega }\)
Lời giải chi tiết:
Phương trình cường độ dòng điện:
\(i = {I_0}\sin \omega t = {I_0}\cos \left( {\omega t - \dfrac{\pi }{2}} \right)\)
Pha ban đầu của cường độ dòng điện là: \( - \dfrac{\pi }{2}\)
Chu kì của dòng điện là: \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{100\pi }} = 0,02\,\,\left( s \right)\)
Trong thời gian \(0,01\,\,s\), dòng điện thực hiện được số chu kì là:
\(\dfrac{t}{T} = \dfrac{{0,01}}{{0,02}} = \dfrac{1}{2} \Rightarrow t = \dfrac{T}{2}\)
Ta có vòng tròn lượng giác:
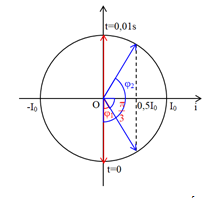
Từ vòng tròn lượng giác, ta thấy từ thời điểm đầu, cường độ dòng điện có giá trị \(0,5{I_0}\) khi vecto quay được các góc:
\(\left\{ \begin{array}{l}{\varphi _1} = \dfrac{\pi }{2} - \dfrac{\pi }{3} = \dfrac{\pi }{6}\,\,\left( {rad} \right) \Rightarrow {t_1} = \dfrac{{{\varphi _1}}}{\omega } = \dfrac{1}{{600}}\,\,\left( s \right)\\{\varphi _2} = \dfrac{\pi }{2} + \dfrac{\pi }{3} = \dfrac{{5\pi }}{6}\,\,\left( {rad} \right) \Rightarrow {t_2} = \dfrac{{{\varphi _2}}}{\omega } = \dfrac{5}{{600}}\,\,\left( s \right)\end{array} \right.\)
Chọn A.
Câu hỏi 32 :
Một điện áp xoay chiều có phương trình \(u = {U_0}cos\left( {100\pi t-\frac{\pi }{3}} \right){\rm{ }}V\). Pha của điện áp tại thời điểm \(t = \frac{1}{{200}}s\) là
- A \(\frac{\pi }{6}\)
- B \( - \frac{\pi }{3}\)
- C \(\frac{\pi }{2}\)
- D \(\frac{{ - \pi }}{6}\)
Đáp án: A
Phương pháp giải:
Thay giá trị \(t = \frac{1}{{200}}s\) vào pha của dao động \(\left( {100\pi t - \frac{\pi }{3}} \right)\)
Lời giải chi tiết:
Thay giá trị \(t = \frac{1}{{200}}s\) vào pha của dao động ta được:
\(\left( {100\pi t - \frac{\pi }{3}} \right) = 100\pi .\frac{1}{{200}} - \frac{\pi }{3} = \frac{\pi }{6}\).
Chọn A.
Câu hỏi 33 :
Đồ thị hình bên mô tả sự biến thiên của cường độ dòng điện xoay chiều theo thời gian. Biểu thức của cường độ dòng điện tức thời có biểu thức
- A \(i = \dfrac{{\sqrt 2 }}{2}cos\left( {100\pi t + \dfrac{\pi }{2}} \right)A.\)
- B \(i = 2cos\left( {100\pi t} \right)A.\)
- C \(i = \dfrac{{\sqrt 2 }}{2}cos\left( {100\pi t} \right)A.\)
- D \(i = 1cos\left( {100\pi t} \right)A.\)
Đáp án: C
Phương pháp giải:
+ Đọc đồ thị i-t
+ Sử dụng biểu thức \(\omega = \dfrac{{2\pi }}{T}\)
+ Viết phương trình cường độ dòng điện
Lời giải chi tiết:
Từ đồ thị ta có:
+ Cường độ dòng điện cực đại: \({I_0} = \dfrac{{\sqrt 2 }}{2}A\)
+ Chu kì dao động: \(T = 0,02s\)
\( \Rightarrow \omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{0,02}} = 100\pi \)
+ Tại thời điểm ban đầu, dòng điện có giá trị cực đại: \( \Rightarrow {i_0} = {I_0}cos\varphi = {I_0} \Rightarrow cos\varphi = 1 \Rightarrow \varphi = 0\)
\( \Rightarrow \) Phương trình cường độ dòng điện: \(i = \dfrac{{\sqrt 2 }}{2}cos\left( {100\pi t} \right)A\)
Chọn C
Câu hỏi 34 :
Một máy biến áp lí tưởng, từ thông xuyên qua mỗi vòng dây của cuộn sơ cấp có biểu thức \(\Phi = 2cos100\pi t\left( {m{\rm{W}}b} \right)\) . Cuộn thứ cấp của máy biến áp có 1000 vòng dây, suất điện động xuất hiện ở cuộn thứ cấp của máy biến áp có giá trị là
- A
\(200\pi cos\left( {100\pi t - \dfrac{\pi }{2}} \right)V.\)
- B
\(200\pi cos\left( {100\pi t} \right)V.\)
- C \(100\pi cos\left( {100\pi t - \dfrac{\pi }{2}} \right)V.\)
- D \(100\pi cos\left( {100\pi t} \right)V.\)
Đáp án: A
Phương pháp giải:
+ Suất điện động: \({e_c} = - \Phi '\)
+ Sử dụng biểu thức máy biến áp lí tưởng: \(\dfrac{{{U_1}}}{{{U_2}}} = \dfrac{{{N_1}}}{{{N_2}}}\)
Lời giải chi tiết:
Ta có,
Suất điện động xuất hiện ở cuộn sơ cấp: \({e_{1c}} = - \Phi ' = \left( {0,2\pi } \right)\sin \left( {100\pi t} \right)\left( V \right)\)
\(\begin{array}{l}\dfrac{{{e_{1c}}}}{{{e_{2c}}}} = \dfrac{{{N_1}}}{{{N_2}}}\\ \Rightarrow {e_{2c}} = \dfrac{{{N_2}}}{{{N_1}}}.{e_{1c}} = 1000.0,2\pi \sin \left( {100\pi t} \right)\\ = 200\pi \sin \left( {100\pi t} \right) = 200\pi cos\left( {100\pi t - \dfrac{\pi }{2}} \right)V\end{array}\)
Chọn A
Câu hỏi 35 :
Một khung dây quay đều trong từ trường đều quanh một trục vuông góc với đường cảm ứng từ. Suất điện động hiệu dụng trong khung là 60V. Nếu giảm tốc độ quay của khung đi 2 lần nhưng tăng cảm ứng từ lên 3 lần thì suất điện động hiệu dụng trong khung có giá trị là:
- A 150V
- B 120V
- C 60V
- D 90V
Đáp án: D
Phương pháp giải:
Suất điện động hiệu dụng trong khung: \(E = \frac{{\omega {\Phi _0}}}{{\sqrt 2 }} = \frac{{\omega .B.S}}{{\sqrt 2 }}\)
Lời giải chi tiết:
Theo bài ra ta có:
\(\begin{array}{*{20}{l}}
{\left\{ {\begin{array}{*{20}{l}}
{E = \frac{{\omega .B.S}}{{\sqrt 2 }} = 60V}\\
{E = \frac{{\omega '.B'.S}}{{\sqrt 2 }} = \frac{{\frac{\omega }{2}.3B.S}}{{\sqrt 2 }} = 1,5E}
\end{array}} \right.}\\
{ \Rightarrow E = 1,5.60 = 90V}
\end{array}\)
Chọn D.
Câu hỏi 36 :
Một khung dây dẫn phẳng quay đều với tốc độ góc ω quanh một trục cố định nằm trong mặt phẳng khung dây, trong một từ trường đều có vec tơ cảm ứng từ vuông góc với trục quay của khung. Suất điện động cảm ứng trong khung có biểu thức e = E0cos(ωt + \(\frac{\pi }{2}\)). Tại thời điểm t = 0, vec tơ pháp tuyến của mặt phẳng khung dây hợp với vec tơ cảm ứng từ một góc bằng
- A 1800
- B 1500
- C 900
- D 450
Đáp án: A
Phương pháp giải:
Suất điện động e chậm pha hơn từ thông góc π/2
Lời giải chi tiết:
Suất điện động e chậm pha hơn từ thông góc π/2 nên tại thời điểm t = 0, pha ban đầu của từ thông là π
Hay vec tơ pháp tuyến của mặt phẳng khung dây hợp với vec tơ cảm ứng từ góc 1800
Chọn A
Câu hỏi 37 :
Một khung dây dẫn phẳng dẹt hình chữ nhật có 500 vòng dây, diện tích mỗi vòng là 220cm2. Khung quay đều với tốc độ 50 vòng/giây quanh một trục đối xứng nằm trong mặt phẳng của khung dây, trong mộ từ trường đều có vec tơ cảm ứng từ \(\overrightarrow{B}\) vuông góc với trục quay và có độ lớn \(\frac{\sqrt{2}}{5\pi }T\) . Suất điện động cực đại trong khung dây bằng:
- A 220V
- B \(110\sqrt{2}V\)
- C 110V
- D \(220\sqrt{2}V\)
Đáp án: D
Phương pháp giải:
Công thức tính suất điện động cực đại: E0 = ωNBS
Lời giải chi tiết:
ω = 50 vòng/giây = 100π rad/s
Suất điện động cực đại: E0 = ωNBS = \(100\pi {{.500.220.10}^{-4}}.\frac{\sqrt{2}}{5\pi }=220\sqrt{2}\)V
Chọn D
Câu hỏi 38 :
Hình bên là đồ thị biểu diễn sự phụ thuộc của điện áp xoay chiều u ở hai đầu một đoạn mạch vào thời gian t. Điện áp hiệu dụng hai đầu đoạn mạch bằng

- A 220 V
- B \(110\sqrt 2 \)V
- C 110 V
- D \(220\sqrt 2 \) V
Đáp án: B
Phương pháp giải:
Phương pháp: Công thức liên hệ giữa điện áp hiệu dụng và điện áp cực đại: \(U = \frac{{{U_0}}}{{\sqrt 2 }}\)
Lời giải chi tiết:
Cách giải :
Từ đồ thị, ta có: \({U_0} = 220(V) \Rightarrow U = \frac{{{U_0}}}{{\sqrt 2 }} = 110\sqrt 2 V\)
Chọn B
Câu hỏi 39 :
Từ thông qua một khung dây dẫn kín có biểu thức \(\Phi = \dfrac{2}{\pi }\cos \left( {100\pi t} \right)\)(\(\Phi \) tính bằng Wb; thời gian \(t\) tính bằng giây). Suất điện động cảm ứng xuất hiện trong khung dây có giá trị hiệu dụng bằng
- A 100V
- B 200V
- C \(100\sqrt 2 \,V\)
- D \(200\sqrt 2 \,V\)
Đáp án: C
Phương pháp giải:
Phương trình của từ thông và suất điện động cảm ứng: \(\left\{ \begin{array}{l}\Phi = {\Phi _0}.cos\left( {\omega t + \varphi } \right)\\{e_{cu}} = - \Phi ' = \omega {\Phi _0}.cos\left( {\omega t + \varphi } \right)\end{array} \right.\)
Suất điện động hiệu dụng: \(E = \dfrac{{{E_0}}}{{\sqrt 2 }} = \dfrac{{\omega {\Phi _0}}}{{\sqrt 2 }}\)
Lời giải chi tiết:
Suất điện động hiệu dụng trong khung dây: \(E = \dfrac{{\omega {\Phi _0}}}{{\sqrt 2 }} = 100\sqrt 2 \)V
Chọn C.
Câu hỏi 40 :
Một khung dây dẫn phẳng dẹt, quay đều quanh trục Δ nằm trong mặt phẳng khung dây, trong một từ trường đều có vec tơ cảm ứng từ vuông góc với trục quay Δ. Từ thông cực đại qua diện tích khung dây bằng \(\frac{11\sqrt{2}}{6\pi }\text{Wb}\) . Tại thời điểm t, từ thông qua diện tích khung dây và suất điện động cảm ứng xuất hiện trong khung dây có độ lớn lần lượt là \(\phi =\frac{11\sqrt{6}}{12\pi }\text{W}b;e=110\sqrt{2}V\) . Tần số của suất điện động cảm ứng xuất hiện trong khung dây là
- A 60Hz
- B 100Hz
- C 50Hz
- D 120Hz
Đáp án: A
Phương pháp giải:
Suất điện động cảm ứng e = - \(\phi '\) nên từ thông và suất điện động cảm ứng vuông pha nên
\({{\left( \frac{\phi }{{{\phi }_{0}}} \right)}^{2}}+{{\left( \frac{e}{{{E}_{0}}} \right)}^{2}}=1\)
Biên độ E0 = \(\omega {{\phi }_{0}}\)
Lời giải chi tiết:
Do từ thông và suất điện động cảm ứng vuông pha nên
\({{\left( \frac{\phi }{{{\phi }_{0}}} \right)}^{2}}+{{\left( \frac{e}{{{E}_{0}}} \right)}^{2}}=1\Rightarrow {{\left( \frac{\frac{11\sqrt{2}}{12\pi }}{\frac{11\sqrt{2}}{6\pi }} \right)}^{2}}+{{\left( \frac{110\sqrt{6}}{{{E}_{0}}} \right)}^{2}}=1\Rightarrow {{E}_{0}}=220\sqrt{2}V\)
Tần số góc \(\omega =\frac{{{E}_{0}}}{{{\phi }_{0}}}=120\pi \Rightarrow f=60Hz\)
Chọn A
Câu hỏi 41 :
Một khung dây dẫn phẳng, dẹt có 500 vòng, mỗi vòng có diện tích 100 cm2. Khung dây quay đều quanh trục nằm trong mặt phẳng khung với tốc độ 3000 vòng/phút, trong một từ trường đều có vectơ cảm ứng từ vuông góc với trục quay và có độ lớn B = 0,1 T. Chọn gốc thời gian lúc pháp tuyến của mặt phẳng khung cùng hướng với vectơ cảm ứng từ. Biểu thức suất điện động cảm ứng xuất hiện trong khung là
- A e = 157cos(100πt - π/2)V
- B e = 157cos(100πt)V
- C e = 15,7cos(100πt - π/2)V
- D e = 15,7cos(100πt)V
Đáp án: A
Phương pháp giải:
Từ thông biên thiên Ф = NBScos(ωt + φ)
Suất điện động cảm ứng e = - Ф’
Lời giải chi tiết:
Theo bài ra ta có N = 500 vòng, S = 100cm2 = 10-2m2; ω = 3000 vòng/phút = 100π rad/s
Gốc thời gian lúc pháp tuyến của mặt phẳng khung cùng hướng với vectơ cảm ứng từ nên φ = 0
Biểu thức từ thông qua khung dây: Ф = NBScos(ωt + φ) = 500.10-2.100π.cos(100πt) Wb
Suất điện động cảm ứng e = - Ф’ = 500.10-2.100π.100π.cos(100πt – π/2) = 157cos(100πt - π/2)V
Chọn A
Câu hỏi 42 :
Một khung dây dẫn quay đều trong từ trường đều và có từ thông qua khung dây biến thiên theo biểu thức: \(\phi = \cos \left( {100t + \frac{\pi }{3}} \right)(m{\rm{W}}b)\) . Hãy viết biểu thức suất điện động cảm ứng xuất hiện trong khung dây dẫn.
- A \(E = 100\cos \left( {100t + {\pi \over 6}} \right)(mV)\)
- B \(E = 100\cos \left( {100t - {\pi \over 6}} \right)(mV)\)
- C \(E = 100\cos \left( {100t - {\pi \over 6}} \right)(V)\)
- D \(E = 100\cos \left( {100t - {\pi \over 6}} \right)(V)\)
Đáp án: B
Phương pháp giải:
Áp dụng công thức tính suất điện động
\(E = \frac{{d\Phi }}{{dt}} = \Phi '\)
Lời giải chi tiết:
Áp dụng công thức tính suất điện động
\(\begin{array}{l}
E = \frac{{d\Phi }}{{dt}} = \Phi ' = \frac{{d\cos \left( {100t + \frac{\pi }{3}} \right)}}{{dt}} = - 100.sin\left( {100t + \frac{\pi }{3}} \right)\\
= 100.\cos \left( {100t + \frac{\pi }{3} - \frac{\pi }{2}} \right) = 100\cos \left( {100t - \frac{\pi }{6}} \right)(mV)
\end{array}\)
Câu hỏi 43 :
Đặt điện áp xoay chiều có giá trị cực đại là 100 V vào hai đầu một đoạn mạch chỉ chứa tụ điện tì cường độ dòng điện chạy qua đoạn mạch có biểu thức i = 2cos(100πt)A . Tại thời điểm điện áp có giá trị 50V và đang tăng thì cường độ dòng điện là
- A 1A
- B
\(\sqrt 3 A\) - C
\( - \sqrt 3 A\) - D –1A
Đáp án: B
Phương pháp giải:
Vì đoạn mạch chỉ chứa tụ điện nên u và i vuông pha với nhau nên ta có :
\({u_C} = 100.\cos \left( {100\pi t - \frac{\pi }{2}} \right)(V)\)
Thay giá trị u = 50V vào phương trình u để tìm pha của u sau đó thay vào phương trình i để tìm cường độ dòng điện tức thời.
Lời giải chi tiết:
Vì đoạn mạch chỉ chứa tụ điện nên u và i vuông pha với nhau nên ta có :
\({u_C} = 100.\cos \left( {100\pi t - \frac{\pi }{2}} \right)(V)\).
Thay giá trị u = 50V vào phương trình u ta được:
\(50 = 100.\cos \varphi {}_u \Rightarrow {\varphi _u} = - \frac{\pi }{3}rad\)
Vậy pha của i và cường độ dòng điện tức thời là :
\({\varphi _i} = {\varphi _u} + \frac{\pi }{2} = \frac{{ 5\pi }}{6} \Rightarrow i = 2.cos\left( {\frac{{ 5\pi }}{6}} \right) = \sqrt 3 A\)
Chọn B.
Câu hỏi 44 :
Một khung dây quay đều trong từ trường \(\;\overrightarrow B \) vuông góc với trục quay của khung với tốc độ n = 1800 vòng/phút. Tại thời điểm t= 0, véc tơ pháp tuyến \(\overrightarrow n \) của mặt phẳng khung dây hợp với \(\;\overrightarrow B \) một góc \(\frac{\pi }{6}\). Từ thông cực đại gửi qua khung dây là 0,01 Wb. Biểu thức của suất điện động của cảm ứng xuất hiện trong khung là
- A
\(e = 0,6\pi \cos (60\pi t - \frac{\pi }{3})\)V - B
\(e = 0,6\pi \cos (30\pi t + \frac{\pi }{2})\)V - C
\(e = 60\pi \cos (30\pi t + \pi )\)V - D
\(e = 0,6\pi \cos (60\pi t - \frac{\pi }{6})\)V
Đáp án: A
Phương pháp giải:
Công thức tính từ thông:
\(\Phi = {\Phi _0}.\cos \left( {\omega t + {\varphi _0}} \right)\)
Tốc độ góc : ω = \(\frac{{1800.2\pi }}{{60}} = 60\pi \)(rad/s)
Suất điện động e = Φ’
Lời giải chi tiết:
Công thức tính từ thông:
\(\Phi = {\Phi _0}.\cos \left( {\omega t + {\varphi _0}} \right)\)
Tốc độ góc : ω = \(\frac{{1800.2\pi }}{{60}} = 60\pi \)(rad/s)
Vì ban đầu vecto pháp tuyến và vec to cảm ứng từ lệch nhau góc 600 nên ta có biểu thức
\(\Phi = 0,01\pi .cos\left( {60\pi t + \frac{\pi }{6}} \right){\rm{W}}b\)
Suất điện động e = Φ’ nên
\(e = - 0,6\pi \sin (60\pi t + \frac{\pi }{6}) = 0,6\pi .\cos \left( {60\pi t - \frac{\pi }{3}} \right)V\)
Câu hỏi 45 :
Đặt vào hai đầu một đoạn mạch điện áp xoay chiều \(u = 200\sqrt 2 \cos \left( {100\pi t + \frac{\pi }{4}} \right)\)(V) thì trong mạch có dòng điện xoay chiều chạy qua với phương trình \(i = 4\sqrt 2 \cos \left( {100\pi t - \frac{\pi }{4}} \right)\)(A). Khi điện áp hai đầu đoạn mạch có giá trị bằng 200 (V) và đang tăng thì cường độ dòng điện qua mạch có độ lớn bằng
- A 4 (A).
- B \(2\sqrt 2 \)(A).
- C \(2\sqrt 3 \)(A).
- D 2(A).
Đáp án: A
Lời giải chi tiết:
Cách giải:
Ta thấy cường độ dòng điện và điện áp giữa hai đầu đoạn mạch vuông pha nhau do đó ta có
\({\left( {\frac{i}{{{I_0}}}} \right)^2} + {\left( {\frac{u}{{{U_0}}}} \right)^2} = 1 = {\rm{\;}} > {\left( {\frac{i}{{4\sqrt 2 }}} \right)^2} + {\left( {\frac{{200}}{{200\sqrt 2 }}} \right)^2} = 1 = {\rm{\;}} > i = 4A\)
Chọn A
Câu hỏi 46 :
Một khung dây dẫn phăng, dẹt có 200 vòng, mỗi vòng có diện tích 500cm2 . Khung dây quay đều quanh trục nằm trong mặt phẳng khung, trong một từ trường đều có vectơ cảm ứng từ vuông góc với trục quay và có độ lớn 5.10-2T. Suất điện động e trong khung có tần số 50 Hz. Chọn gốc thời gian lúc pháp tuyến của mặt phẳng khung hợp với vecto cảm ứng từ góc \(\dfrac{\pi }{3}\). Biểu thức của e là :
- A \(e = 50\pi \sqrt 2 .\cos \left( {100\pi t - \dfrac{\pi }{6}} \right)V\)
- B \(e = 50\pi \sqrt 2 .\cos \left( {100\pi t + \dfrac{\pi }{3}} \right)V\)
- C \(e = 50\pi .\cos \left( {100\pi t + \dfrac{\pi }{3}} \right)V\)
- D \(e = 50\pi .\cos \left( {100\pi t - \dfrac{\pi }{6}} \right)V\)
Đáp án: D
Phương pháp giải:
Từ thông qua khung dây:
\(\Phi = NBS.\cos \left( {\overrightarrow n ;\overrightarrow B } \right) = NBS.\cos \left( {\omega t + \varphi } \right) = {\Phi _0}\cos \left( {\omega t + \varphi } \right)\)
Suất động trong khung dây:
\(e = - \dfrac{{d\Phi }}{{dt}} = - \Phi ' = \omega NBS.\sin \left( {\omega t + \varphi } \right) = \omega NBS.\cos \left( {\omega t + \varphi - \dfrac{\pi }{2}} \right) = {E_0}.\cos \left( {\omega t + \varphi - \dfrac{\pi }{2}} \right)\)
Lời giải chi tiết:
Ta có : \(\left\{ \begin{array}{l}\omega = 2\pi f = 100\pi \,\left( {rad/s} \right)\\N = 200\\S = 500c{m^2} = 0,05{m^2}\\B = {5.10^{ - 2}}T\\\varphi = \left( {\overrightarrow n ;\overrightarrow B } \right) = \dfrac{\pi }{3}\end{array} \right.\)
Suất điện động cực đại:\({E_0} = \omega NBS = 100\pi {.200.5.10^{ - 2}}.0,05 = 50\pi \,\left( V \right)\)
Biểu thức của suất điện động cảm ứng là:
\(e = 50\pi .\cos \left( {100\pi t + \dfrac{\pi }{3} - \dfrac{\pi }{2}} \right) = 50\pi .\cos \left( {100\pi t - \dfrac{\pi }{6}} \right)V\)
Chọn D.
Câu hỏi 47 :
Điện áp giữa hai đầu một đoạn mạch có biểu thức \(u = 220\sqrt 2 .\cos \left( {100\pi t} \right)V\) , t tính bằng giây (s). Tại một thời điểm t1điện áp có giá trị tức thời là \(110\sqrt 2 V\) và đang giảm. Vào thời điểm \({t_2} = {t_1} + 0,005s\) điện áp có giá trị tức thời bằng bao nhiêu?
- A \( - 110{\sqrt 6 _{}}V\)
- B \( + 110{\sqrt 3 _{}}V\)
- C \( - 110{\sqrt 3 _{}}V\)
- D \(+ 110{\sqrt 6 _{}}V\)
Đáp án: A
Phương pháp giải:
Áp dụng phương pháp vecto quay.
Tìm chu kì, tìm vị trí của điện áp tức thời tại t1 và t2, góc mà vecto quay quay được xác định:
\(\Delta \varphi = \frac{{\Delta t}}{T}.2\pi \)
Lời giải chi tiết:
Chu kì dao động :
\(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{100\pi }} = 0,02s\)
Vì \({t_2} = {t_1} + 0,005s = {t_1} + \frac{T}{4}\).
Suy ra góc mà vecto quay quay được là :
\(\Delta \varphi = \frac{1}{4}.2\pi = \frac{\pi }{2}\)
Ta có hình vẽ:

Ta có góc α có giá trị là
\(\alpha = \arccos \frac{{110\sqrt 2 }}{{220\sqrt 2 }} = \frac{\pi }{3}\)
Vậy góc β có giá trị là
\(\beta = \pi - \frac{\pi }{3} - \frac{\pi }{2} = \frac{\pi }{6}\)
Khi đó giá trị điện áp hiệu dụng là :
\(u = - 220\sqrt 2 .\cos \frac{\pi }{6} = - 110{\sqrt 6 _{}}\left( V \right)\)
Chọn A.
Câu hỏi 48 :
Người ta làm nóng 1 kg nước thêm 10C bằng cách cho dòng điện 2A đi qua một điện trở 6Ω. Biết nhiệt dung riêng của nước là 4200 J/kg.K. Thời gian cần thiết là
- A 17,5s
- B 17,5 phút.
- C 175 phút.
- D 175s
Đáp án: D
Phương pháp giải:
Nhiệt lượng nước thu vào : \(Q = m.c.\Delta t\)
Điện năng tiêu thụ của dòng điện : \(A = {I^2}Rt\)
Ta có : \(A = Q \Rightarrow t\)
Lời giải chi tiết:
Nhiệt lượng mà 1kg nước thu vào để tăng thêm 10C là :
\(Q = m.c.\Delta t = 1.4200.1 = 4200J\)
Điện năng dòng điện tiêu thụ :
\(A = {I^2}Rt = {2^2}.6.t = 24.t\,\,\left( J \right)\)
Ta có : \(A = Q \Leftrightarrow 24.t\, = 4200 \Rightarrow t = 175s\)
Chọn D.
Câu hỏi 49 :
Một khung dây dẫn hình chữ nhật có 100 vòng dây, diện tích mỗi vòng dây là 125 cm2. Cho khung dây quay đều quanh một trục đối xứng (thuộc mặt phẳng của khung) với tốc độ góc 100π rad/s, trong từ trường đều có vectơ cảm ứng từ vuông góc với trục quay và có độ lớn cảm ứng từ là 0,4 T. Suất điện động hiệu dụng giữa hai đầu khung dây xấp xỉ bằng
- A 220 V
- B 314 V
- C 111 V.
- D 157 V
Đáp án: C
Phương pháp giải:
Công thức tính suất điện động tạo bởi khung dây quay trong từ trường :
E0 = ωNBS
Liên hệ giữa giá trị hiệu dụng và giá trị cực đại : \(E=\frac{{{E}_{0}}}{\sqrt{2}}\)
Lời giải chi tiết:
Suất điện động hiệu dụng giữa hai đầu khung dây :
\(E=\frac{{{E}_{0}}}{\sqrt{2}}=\frac{\omega NBS}{\sqrt{2}}=\frac{100\pi {{.100.0,4.125.10}^{-4}}}{\sqrt{2}}=111V\)
Câu hỏi 50 :
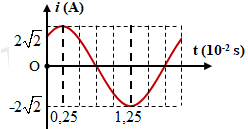
Hình bên là đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện xoay chiều chạy qua đoạn mạch vào thời gian t. Cường độ dòng điện hiệu dụng chạy qua mạch bằng:
- A \(2A\)
- B \(2\sqrt 2 A\)
- C \(\sqrt 2 A\)
- D \(4A\)
Đáp án: A
Phương pháp giải:
Cường độ dòng điện hiệu dụng: \(I = \dfrac{{{I_0}}}{{\sqrt 2 }}\)
Lời giải chi tiết:
Từ đồ thị ta có: \({I_0} = 2\sqrt 2 A \Rightarrow I = \dfrac{{{I_0}}}{{\sqrt 2 }} = \dfrac{{2\sqrt 2 }}{{\sqrt 2 }} = 2A\)
Chọn A.