Câu hỏi 1 :
Biết cường độ âm chuẩn là 10-12 w/m2. Khi cường độ âm tại một điểm là 10-4 W/m2 thì mức cường độ âm tại điểm đó bằng
- A 80 dB.
- B 50 dB.
- C 60 dB.
- D 70 dB.
Đáp án: A
Lời giải chi tiết:
Đáp án A
Phương pháp : Công thức tính mức cường độ âm
Mức cường độ âm: 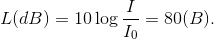
Câu hỏi 2 :
Một nguồn âm S có công suất P, sóng âm lan truyền theo mọi phía. Mức cường độ âm tại điểm cách S 1m là 100 dB. Cho cường độ âm chuẩn I0 = 10-12 W/m2. Cường độ âm tại điểm cách S 10m là:
- A 2W/m2
- B 1,5W/m2
- C 1W/m2
- D 2,5W/m2
Đáp án: C
Phương pháp giải:
Công thức tính mức cường độ âm và mức cường độ âm:
\(L = 10.\log {I \over {{I_0}}};I = {P \over {4\pi {R^2}}}\)
Lời giải chi tiết:
Ta có: \(L = 100 = 10.\log {I \over {{I_0}}} \Rightarrow {I_1} = {10^{ - 2}}({\rm{W}}/{m^2})\)
\(\left\{ \matrix{
{I_1} = {P \over {4\pi R_1^2}} \hfill \cr
{I_2} = {P \over {4\pi R_2^2}} \hfill \cr} \right. \Rightarrow {{{I_2}} \over {{I_1}}} = {\left( {{{{R_1}} \over {{R_2}}}} \right)^2} \Leftrightarrow {{{I_2}} \over {100}} = {\left( {{1 \over {10}}} \right)^2} = {1 \over {100}} \Rightarrow {I_2} = 1({\rm{W}}/{m^2})\)
Chọn C
Câu hỏi 3 :
Một nguồn âm gây ra cường độ âm tại M là IM ; tại N là IN . Mối liên hệ giữa cường độ âm tại M và N lần lượt là
- A \({L_M} - {L_N} = 10\lg {{{I_N}} \over {{I_M}}}(dB)\)
- B \({{{L_M}} \over {{L_N}}} = 10\lg {{{I_N}} \over {{I_M}}}(dB)\)
- C \({{{L_M}} \over {{L_N}}} = 10\lg {{{I_M}} \over {{I_N}}}(dB)\)
- D \({L_M} - {L_N} = 10\lg {{{I_M}} \over {{I_N}}}(dB)\)
Đáp án: D
Lời giải chi tiết:
\({L_M} - {L_N} = 10\lg {{{I_M}} \over {{I_N}}}(dB)\)
Câu hỏi 4 :
Một sóng âm truyền trong không khí. Mức cường độ âm tại điểm M và tại điểm N lần lượt là 20dB và 50dB. Cường độ âm tại N lớn hơn cường độ âm tại M
- A 30 lần
- B 1000 lần
- C 2,5 lần
- D 10000 lần
Đáp án: B
Phương pháp giải:
Phương pháp: Sử dụng công thức hiệu mức cường độ âm ${L_N} - {L_M} = 10\log \frac{{{I_N}}}{{{I_M}}}$
Lời giải chi tiết:
Ta có hiệu mức cường độ âm tại N và M là:
${L_N} - {L_M} = 10\log \frac{{{I_N}}}{{{I_M}}} = 50 - 20 = 30 \to \log \frac{{{I_N}}}{{{I_M}}} = 3 \to \frac{{{I_N}}}{{{I_M}}} = {10^3}$
=> Chọn B
Câu hỏi 5 :
Một nguồn âm điểm O phát âm với công suất không đổi, âm truyền trong môi trường đẳng hướng không hấp thụ âm. Tại M và N mức cường độ âm lần lượt là 40 db và 20 dB. Tỷ số OM/ON là:
- A 10
- B 0,01
- C 100
- D 0,1
Đáp án: D
Phương pháp giải:
Sử dụng công thức xác định hiệu mức cương độ âm: \({L_2} - {L_1} = 10\log {{{I_2}} \over {{I_1}}}(dB)\)
Sử dụng công thức tính cường độ âm: \(I = {P \over {4\pi {r^2}}}\)
Lời giải chi tiết:
Ta có: \({L_M} - {L_N} = 20 = 10\log {{{I_M}} \over {{I_N}}} = 10\log {{{r_N}^2} \over {{r_M}^2}} = 10\log {{O{N^2}} \over {O{M^2}}} \to {{O{N^2}} \over {O{M^2}}} = {10^2} \to ON = 10.OM\)
(với \(I = {P \over {4\pi {r^2}}}\))
=> Chọn D
Câu hỏi 6 :
Nguồn âm S phát ra âm có công suất \(P = 4\pi {.10^{ - 5}}{\rm{W}}\) không đổi, truyền đẳng hướng về mọi phương. Cho cường độ âm chuẩn \({I_0} = {10^{ - 12}}{\rm{W}}/{m^2}\) . Điểm M cách nguồn S một đoạn 1m có mức cường độ âm là:
- A 50dB
- B 60dB
- C 70dB
- D 80dB
Đáp án: C
Phương pháp giải:
Cường độ âm I = P/(4πr2)
Mức cường độ âm: L = 10.log(I/I0)
Lời giải chi tiết:
Mức cường độ âm tại M : \({L_M} = 10.\log {{{I_M}} \over {{I_0}}} = 10.\log {P \over {4\pi .{r^2}.{I_0}}} = 10.\log {{4\pi {{.10}^{ - 5}}} \over {4\pi {{.1}^2}{{.10}^{ - 12}}}} = 70dB\)
Câu hỏi 7 :
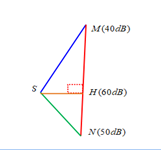
Cho 3 điểm A,B,C thẳng hang, theo thứ tự xa dần nguồn âm.Mức cường độ âm tại A,B,C lần lượt là 40dB; 35,9dB và 30dB. Khoảng cách giữa AB là 30m, và khoảng cách giữa BC là:
- A 78m
- B 108m
- C 40m
- D 65m
Đáp án: A
Lời giải chi tiết:
Đáp án A
Giả sử nguồn âm tại O có công suât P
$$I ={P \over {4\pi {R^2}}}$$
LA - LB = 10lg = 4,1 dB -> 2lg = 0,41-> RB = 100,205RA
LA – LC = 10lg = 10 dB -> 2lg = 1-> RC = 100,5 RA
RB – RA = ( 100,205 – 1) RA = BC = 30m -> RA = 49,73 m
RC – RB = (100,5 – 100,205) RA -> BC = (100,5 – 100,205) 49,73 = 77,53 m » 78 m
Câu hỏi 8 :
Cường độ âm tại một điểm trong môi trường truyền âm là 10-5 W/m2. Biết cường độ âm chuẩn là I0 = 10-12 W/m2. Mức cường độ âm tại điểm đó bằng.
- A 80dB
- B 70dB.
- C 50dB.
- D 60dB
Đáp án: B
Phương pháp giải:
Mức cường độ âm L = 10.log(I/I0)
Lời giải chi tiết:
Mức cường độ âm tại điểm đó là: \(L = 10.\log ({I \over {{I_0}}}) = 10.log({{{{10}^{ - 5}}} \over {{{10}^{ - 12}}}}) = 70dB.\)
Câu hỏi 9 :
Tại điểm O trong môi trường đẳng hướng, không hấp thụ âm, có 2 nguồn âm điểm, giống nhau với công suất phát âm không đổi. Tại điểm A có mức cường độ âm 20 dB. Để tại trung điểm M của đoạn OA có mức cường độ âm là 30 dB thì số nguồn âm giống các nguồn âm trên cần đặt thêm tại O bằng
- A 4
- B 3
- C 5
- D 7
Đáp án: B
Phương pháp giải:
Phương pháp : Áp dụng công thức tính mức cường độ âm
Lời giải chi tiết:
Đáp án B
Áp dụng công thức tính mức cường độ âm
Ta có \(20 = 10\log \left( {{{2p} \over {4\pi O{A^2}{I_o}}}} \right)\);\(30 = 10\log \left( {{{np} \over {4\pi O{M^2}{I_o}}}} \right) = 10\log \left( {{{np} \over {4\pi {{O{A^2}} \over 4}{I_o}}}} \right) = 10\log \left( {{{4np} \over {4\pi O{A^2}{I_o}}}} \right)\)
=>\(30 - 10 = 10\log \left( {{{4np} \over {2p}}} \right) = 10{\mathop{\rm l}\nolimits} og2n =>n=5\)
Câu hỏi 10 :
Một người đứng trước cách nguồn âm S một đoạn D. Nguồn này phát sóng cầu. Khi người đó đi lại gần nguồn âm 50m thì thấy cường độ âm tăng lên gấp đôi. Khoảng cách d là:
- A 171m.
- B 29,3m.
- C 222m
- D 22,5 m
Đáp án: A
Phương pháp giải:
Sử dụng công thức tính cường độ âm
Lời giải chi tiết:
\({{{I_1}} \over {{I_2}}} = {\left( {{{{r_2}} \over {{r_1}}}} \right)^2} \Leftrightarrow {1 \over 2} = {\left( {{{{r_2}} \over {{r_1}}}} \right)^2} \Rightarrow {{{r_2}} \over {{r_1}}} = {1 \over {\sqrt 2 }} \Leftrightarrow {r_2} = {1 \over {\sqrt 2 }}d\)
Mà d – r2 = 50m nên: \(d - {1 \over {\sqrt 2 }}.d = 50 \Rightarrow d = {{50} \over {1 - {1 \over {\sqrt 2 }}}} = 171m\)
Câu hỏi 11 :
Một nguồn âm đặt tại O trong môi trường đẳng hướng. Hai điểm M và N trong môi trường tạo với O thành một tam giác đều. Mức cường độ âm tại M và N đều bằng 14,75 dB. Mức cường độ âm lớn nhất mà một máy thu thu được khi đặt tại một điểm trên đoạn MN bằng
- A 18 dB.
- B 16,8 dB
- C 16 dB
- D 18,5 dB
Đáp án: C
Phương pháp giải:
Phương pháp :Áp dụng công thức tính mức cường độ âm
Lời giải chi tiết:
Đáp án C
Cách giải :
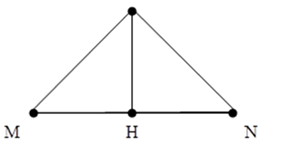
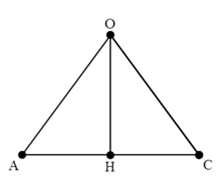
Tam giác ONM là tam giác vuông cân nên ta dễ dàng chứng minh được \(OM = \frac{2}{{\sqrt 3 }}OH\)à \({L_H} = {L_M} + 20\log \frac{{OM}}{{OH}} = 14,75 + 20\log \frac{2}{{\sqrt 3 }} = 16dB\)
Câu hỏi 12 :
Trên một đường thẳng cố định trong môi trường đẳng hướng, không hấp thụ và phản xạ âm, một máy thu ở cách nguồn âm một khoảng d thu được âm có mức cường độ âm là L, khi dịch chuyển máy thu ra xa nguồn âm thêm 9 m thì mức cường độ âm thu được là L – 20 dB. Khoảng cách d là
- A 8 m.
- B 1 m.
- C 9 m
- D 10 m.
Đáp án: B
Phương pháp giải:
áp dụng công thức tính mức cường độ âm \(L = 10\log {P \over {{I_0}4\pi {d^2}}}.\)
Lời giải chi tiết:
Đáp án B
+ Ta có \(L = 10\log {P \over {{I_0}4\pi {d^2}}} \Rightarrow {L_A} - {L_B} = 20 = 20\log {{d + 9} \over d} \Rightarrow d = 1\,\,m.\)
Câu hỏi 13 :
Nguồn điểm O phát sóng đẳng hướng ra không gian. Ba điểm O, A và B nằm trên một phương truyền sóng (A, B cùng phía so với O, AB = 70 m). Điểm M là một điểm thuộc AB cách O một khoảng 60 m có cường độ âm 1,5 m/s2. Năng lượng của sóng âm giới hạn bởi 2 mặt cầu tâm O đi qua A và B, biết vận tốc truyền âm trong không khí là 340 m/s và môi trường không hấp thụ âm.
- A 5256 J.
- B 13971 J.
- C 16299 J.
- D 14971 J.
Đáp án: B
Phương pháp giải:
áp dụng công thức tính cường độ âm tại một điểm \(I = {P \over {4\pi r_{}^2}}\)
Lời giải chi tiết:
Đáp án B
+ Cường độ âm tại điểm M: \({I_M} = {P \over {4\pi r_M^2}} \to P = 4\pi r_M^2{I_M}\)
+ Năng lượng của sóng âm trong vùng không gian giới hạn bởi hai mặt cầu là: \(E = Pt \to E = 4\pi r_M^2{I_M}t = 4\pi r_M^2{I_M}{{AB} \over v} = 4\pi {.60^2}.1,5.{{70} \over {340}} = 13971J.\)
Câu hỏi 14 :
Tại một vị trí trong môi trường truyền âm, khi mức cường độ âm tăng thêm 20 dB thì cường độ âm tại đó tăng gấp bao nhiêu lần so với giá trị ban đầu ?
- A 10 lần
- B 20 lần
- C 100 lần
- D 200 lần
Đáp án: C
Phương pháp giải:
Áp dụng công thức tính mức cường độ âm \(L = 10\log {I \over {{I_0}}}\)
Lời giải chi tiết:
Đáp án C
+ Ta có \( L = 10\log {I \over {{I_0}}} = > {{I'} \over I} = {10^{{{\Delta L} \over {10}}}} = {10^{{{20} \over {10}}}} = 100\)
Câu hỏi 15 :
Một nguồn âm coi là nguồn âm điểm phát âm đều theo mọi phương, môi trường không hấp thụ âm. Mức cường độ âm tại điểm M lúc đầu là 80 dB. Nếu tăng công suất của nguồn âm lên 20% thì mức cường độ âm tại M là
- A 80,8 dB
- B 95,0 dB.
- C 62,5 dB.
- D 125 dB.
Đáp án: A
Lời giải chi tiết:
Đáp án A
+ Ta có
\(\left\{ \matrix{
L = 10\log {P \over {{I_0}4\pi {r^2}}} = 80 \hfill \cr
L' = 10\log {{1,2P} \over {{I_0}4\pi {r^2}}} \hfill \cr} \right. \to L' = 80 + 10\log 1,2 = 80,8\,\,dB.\)
Câu hỏi 16 :
Tại một vị trí trong môi trường truyền âm, một sóng âm có cường độ âm I. Biết cường độ âm chuẩn là I0. Mức cường độ âm L của sóng âm này tại vị trí đó được tính bằng công thức
- A \(L\left( B \right) = \lg {{{I_0}} \over I}\)
- B \(L\left( {dB} \right) = 10\lg {{{I_0}} \over I}\)
- C \(L\left( {dB} \right) = \lg {I \over {{I_0}}}\)
- D \(L\left( B \right) = 10\lg {I \over {{I_0}}}\)
Đáp án: C
Lời giải chi tiết:
Đáp án C
+ Mức cường độ âm tại vị trí có cường độ âm I được xác định bằng biểu thức \(L = 10\log {I \over {{I_0}}}\,\,dB.\)
Câu hỏi 17 :
Cường độ âm tại một điểm trong môi trường truyền âm là 10-4 W/m2. Biết cường độ âm chuẩn là 10-12 W/m2. Mức cường độ âm tại điểm đó bằng
- A 8 dB.
- B 0,8 dB.
- C 80 dB.
- D 80 B.
Đáp án: C
Lời giải chi tiết:
Đáp án C
+ Mức cường độ âm tại vị trí có cường độ âm I là \(L = 10\log {I \over {{I_0}}} = 10\log {{{{10}^{ - 4}}} \over {{{10}^{ - 12}}}} = 80\,\,dB.\)
Câu hỏi 18 :
Tại vị trí O trong một nhà máy, một còi báo cháy (được coi như một nguồn điểm) phát sóng âm với công suất không đổi. Từ bên ngoài một thiết bị xác định mức cường độ âm chuyển động thẳng biến đổi đều từ M hướng đến O theo hai giai đoạn với vận tốc ban đầu bằng không và gia tốc có độ lớn 3,75 m/s2 cho biết khi dừng lại tại N (cổng nhà máy). Biết NO = 15 m và mức cường độ âm do còi phát ra tại N lớn hơn mức cường độ âm tại M là 20 dB. Cho rằng môi trường truyền âm là đẳng hướng và không hấp thụ âm. Thời gian thiết bị đó chuyển động từ M đến N có giá trị gần giá trị nào nhất
- A 20 s.
- B 25 s.
- C 15 s.
- D 10 s.
Đáp án: D
Lời giải chi tiết:
Đáp án D
+ Ta có : \({L_N} - {L_M} = 20\log \left( {{{OM} \over {ON}}} \right) \Rightarrow OM = 10ON\)
Vậy MN = 135 m
Xe chuyển động thành hai giai đoạn trên MN, nửa giai đoạn đầu là nhanh dần đều, nửa giai đoạn sau là chậm dần đều \( \to t = 2\sqrt {{{MN} \over {2{\rm{a}}}}} = 2\sqrt {{{135} \over {2.3,75}}} = 8,48\,\,s\)
Câu hỏi 19 :
Cho một nguồn âm đẳng hướng trong không gian đặt tại O. Biết O, A, B thẳng hàng; mức cường độ âm của hai điểm A, B lần lượt là 40 dB và 20 dB. Mức cường độ âm tại trung điểm của AB là:
- A 28,3 dB
- B 25,4 dB
- C 30,0 dB
- D 32,6 dB
Đáp án: B
Phương pháp giải:
Áp dụng công thức tính mức cường độ âm, cường độ âm.
Lời giải chi tiết:
Ta có: \({L_A} = 10\log ({{{I_A}} \over {{I_0}}}) = 40dB \Rightarrow {I_A} = {10^{ - 8}}{\rm{W}}/{m^2};{L_B} = 10\log ({{{I_B}} \over {{I_0}}}) = 20dB \Rightarrow {I_B} = {10^{ - 10}}{\rm{W}}/{m^2}\)
Mà :
\(\eqalign{
& {{{I_A}} \over {{I_B}}} = {{r_B^2} \over {r_A^2}} \Rightarrow {{{r_B}} \over {{r_A}}} = 10 \Rightarrow {r_B} = 10{r_A} \cr
& {r_C} = {{{r_A} + {r_B}} \over 2} = {{11} \over 2}{r_A} \Rightarrow {{{I_A}} \over {{I_C}}} = {{r_C^2} \over {r_A^2}} = {{{{11}^2}} \over 4} \Rightarrow {I_C} = {4 \over {{{11}^2}}}.{I_A} \cr
& {L_C} = 10\log ({{{I_C}} \over {{I_0}}}) = 10log({{{4 \over {{{11}^2}}}.{I_A}} \over {{I_0}}}) = 10.{\rm{[}}log({{{I_A}} \over {{I_0}}}) + log\left( {{4 \over {{{11}^2}}}} \right){\rm{] = }}25,1dB \cr} \)
Câu hỏi 20 :
Một nguồn âm đẳng hướng đặt tại một điểm trong không khí, điểm M nằm trong môi trường truyền âm có cường độ âm bằng 10-8 W/m2. Biết cường độ âm chuẩn I0 = 10-12 W/m2. Mức cường độ âm tại M là
- A 50dB
- B 40dB
- C 60dB
- D 40dB
Đáp án: D
Phương pháp giải:
Mức cường độ âm \(L = 10\log {I \over {{I_0}}}(dB)\)
Lời giải chi tiết:
Mức cường độ âm tại M: \({L_M} = 10\log {{{I_M}} \over {{I_0}}}(dB) = 10\log {{{{10}^{ - 8}}} \over {{{10}^{ - 12}}}} = 40(dB)\)
Câu hỏi 21 :
Một nguồn âm coi là nguồn âm điểm phát âm đẳng hướng trong không gian. Môi trường không hấp thụ âm. Mức cường độ âm tại M lúc đầu là 50dB. Nếu tăng công suất của nguồn âm lên 30% thì mức cường độ âm tại M bằng
- A 61,31dB
- B 50,52dB
- C 51,14dB
- D 50,11dB
Đáp án: C
Phương pháp giải:
Công thức tính mức cường độ âm: \(L = 10\log {I \over {{I_0}}} = 10\log {P \over {4\pi {R^2}{I_0}}}\)
Lời giải chi tiết:
+ Lúc đầu, mức cường độ âm tại M: \({L_M} = 10\log {P \over {4\pi {R^2}{I_0}}} = 50dB\)
+ Sau khi tăng công suất của nguồn âm lên 30%: \({L_M}' = 10\log {{P + 0,3P} \over {4\pi {R^2}{I_0}}} = 10\log 1,3 + 10\log {P \over {4\pi {R^2}{I_0}}} = 1,14 + 50 = 51,14dB\)
Câu hỏi 22 :
Trên một đường thẳng cố định trong môi trường đẳng hướng, không hấp thụ và phản xạ âm, một máy thu ở cách nguồn âm một khoảng d thu được âm có mức cường độ âm là L; khi dịch chuyển máy thu ra xa nguồn âm thêm 9m thì mức cường độ âm thu được là L- 20 dB, Khoảng cách d là
- A 1m
- B 8m
- C 10m
- D 9m
Đáp án: A
Phương pháp giải:
sử dụng công thức tính mức cường độ âm và cường độ âm
Lời giải chi tiết:
\(\eqalign{
& {L_A} = 10\log {{{I_A}} \over {{I_O}}};{L_B} = 10\log {{{I_B}} \over {{I_O}}} = {L_A} - 20 \cr
& {{{I_A}} \over {{I_B}}} = {{r_B^2} \over {r_A^2}} = {{{{\left( {r + 9} \right)}^2}} \over {{r^2}}} \cr
& 10\log {{{I_A}} \over {{I_B}}} = 10\log {{{I_A}} \over {{I_O}}} - 10\log {{{I_B}} \over {{I_O}}} \cr
& 20\log {{r + 9} \over r} = 20 \Rightarrow {{r + 9} \over r} = 10 \Rightarrow r = 1m \cr} \)
Câu hỏi 23 :
Trong một môi trường đẳng hướng và không hấp thụ âm, có ba điểm theo thứ tự A, B, C thẳng hàng. Một nguồn âm điểm phát âm có công suất P được đặt tại B thì mức cường độ âm tại A là 40 dB, tại C là 20 dB. Mức cường độ âm tại trung điểm AC có giá trị gần đúng bằng
- A 53dB.
- B 27dB.
- C 34dB.
- D 42dB.
Đáp án: B
Phương pháp giải:
Sử dụng lí thuyết về sự truyền âm
Lời giải chi tiết:
Ta có \({L_A} - {L_B} = 20\lg \frac{{{r_B}}}{{{r_A}}} \Leftrightarrow 20 = 20\lg \frac{{{r_B}}}{{{r_A}}} \Leftrightarrow \frac{{{r_B}}}{{{r_A}}} = 10 \Rightarrow {r_B} = 10{r_A}\)
C là trung điểm của AB nên \({r_C} = \frac{{{r_A} + {r_B}}}{2} = \frac{{{r_A} + 10{r_A}}}{2} = 5,5{r_A}\)
Suy ra \({L_A} - {L_C} = 20\lg \frac{{{r_C}}}{{{r_A}}} = 20\lg \frac{{5,5{r_A}}}{{{r_A}}} = 20\lg 5,5 = 14,8 \Rightarrow {L_C} = 25,2dB\)
Chọn B
Câu hỏi 24 :
Cho tam giác ABC vuông cân tại A nằm trong một môi trường truyền âm. Một nguồn âm điểm O có công suất không đổi phát âm đẳng hướng đặt tại B khi đó một người M đứng tại C nghe được âm có mức cường độ âm là 40dB. Sau đó di chuyển nguồn O trên đoạn AB và người M di chuyển trên đoạn AC sao cho BO = AM. Mức cường độ âm lớn nhất mà người đó nghe được trong quá trình cả hai di chuyển bằng
- A 56,6 dB
- B 46,0 dB
- C 42,0 dB
- D 60,2 dB
Đáp án: B
Phương pháp giải:
Công thức tính mức cường độ âm: \(L = 10.\log {I \over {{I_0}}} = 10.\log {P \over {4\pi .{r^2}}}\)
Lời giải chi tiết:
Khi nguồn âm O đặt tại B, người đứng tại C nghe được âm có mức cường độ âm: \({L_C} = 10.\log {P \over {4\pi .B{C^2}}} = 40dB\)
Khi di chuyển nguồn O trên đoạn AB và người M di chuyển trên đoạn AC sao cho BO = AM thì mức cường độ âm người nghe được: \({L_M} = 10.\log {P \over {4\pi .O{M^2}}}\)
Ta có: \({\left( {{L_M}} \right)_{\max }} \Leftrightarrow O{M_{\min }}\)
∆ABC vuông cân tại A có BO = AM => OMmin <=> OM là đường trung bình của ∆ABC
\(\eqalign{
& \Rightarrow O{M_{\min }} = {{BC} \over 2} \Rightarrow {\left( {{L_M}} \right)_{m{\rm{ax}}}} = 10.\log {P \over {4\pi .{{\left( {{{BC} \over 2}} \right)}^2}}} = 10.\log {{4P} \over {4\pi .B{C^2}}} \cr
& \Rightarrow {\left( {{L_M}} \right)_{\max }} - {L_C} = 10.\log {{4P} \over {4\pi .B{C^2}}} - 10.\log {P \over {4\pi .B{C^2}}} = 10\log 4 \Rightarrow {\left( {{L_M}} \right)_{\max }} = {L_C} + 10\log 4 \cr
& \Rightarrow {\left( {{L_M}} \right)_{\max }} = 40 + 10\log 4 = 46dB \cr} \)
Câu hỏi 25 :
Một nguồn điểm S phát sóng âm đẳng hướng ra không gian. Hai điểm A, B cách nhau 100 m cùng nằm trên phương truyền sóng cùng phía với S. Điểm M là trung điểm của AB và cách nguồn 70 m có mức cường độ âm là 40 dB. Biết cường độ âm chuẩn I0 = 10-12 W/m2 và tốc độ truyền âm trong không khí là 340 m/s và môi trường không hấp thụ âm. Năng lượng của sóng âm trong khoảng không gian giới hạn của hai mặt cầu tâm qua A và B là
- A 181 mJ.
- B 181 µJ.
- C 207 mJ.
- D 207 µJ.
Đáp án: B
Phương pháp giải:
Áp dụng công thức tính mức cường độ âm \({L_M} = 10\log {P \over {{I_0}4\pi S{M^2}}}\)
Lời giải chi tiết:
Đáp án B
+ Mức cường độ âm tại điểm M là trung điểm của AB được xác định bởi:
\({L_M} = 10\log {P \over {{I_0}4\pi S{M^2}}} \leftrightarrow 40 = 10\log {P \over {{{10}^{ - 12}}4\pi {{70}^2}}} \to P = 6,{2.10^{ - 4}}{\rm{W}}\)
→ Năng lượng giới hạn bởi hai mặt cầu \(E = Pt = P{{AB} \over v} = 6,{2.10^{ - 4}}{{100} \over {340}} = 1,{81.10^{ - 4}}J\)
Câu hỏi 26 :
Một thiết bị dùng để xác định mức cường độ âm được phát ra từ một nguồn âm đẳng hướng đặt tại điểm O, thiết bị bắt đầu chuyển động nhanh dần đều từ điểm M đến điểm N với gia tốc 3 m/s2, biết \(OM = {{ON} \over {\sqrt 3 }} = 12\,m\) và ∆OMN vuông tại O. Chọn mốc thời gian kể từ thời điểm máy bắt đầu chuyển động thì mức cường độ âm lớn nhất mà máy đo được khi đi từ M đến N là bao nhiêu và tại thời điểm nào? Biết mức cường độ âm đo được tại M là 60 dB.
- A 66,02 dB và tại thời điểm 2 s.
- B 65,25 dB và tại thời điểm 4 s.
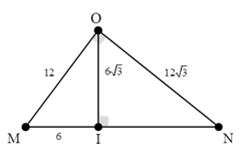
- C 66,02 dB và tại thời điểm 2,6 s.
- D 61,25 dB và tại thời điểm 2 s.
Đáp án: D
Phương pháp giải:
Áp dụng công thức tính mức cường độ âm \({{\rm{L}}_{\rm{}}} = 10\log {{\rm{I}} \over {{I_0}}}{\rm{.}}\)
Lời giải chi tiết:
Đáp án D.
+ Khi xác định mức cường độ âm di chuyển từ M đến N thì thu được mức cường độ âm lớn nhất tại I với I là đường vuông góc hạ từ O xuống MN.
Áp dụng hệ thức lượng trong tam giác vuông ta tìm được MI = 6 cm.\({\rm{OI = 6}}\sqrt {3{\rm{ }}} {\rm{cm}}{\rm{.}}\)
+ Mức cường độ âm tại:
\({\rm{I: }}{{\rm{L}}_{\rm{I}}} = {{\rm{L}}_{\rm{M}}} + 20\log {{{\rm{OM}}} \over {{\rm{IM}}}} = 60 + 20\log {{12} \over {6\sqrt 3 }} = 61,25{\rm{dB}}{\rm{.}}\)
+ Thời gian để thiết bị chuyển động từ M đến I:
\({\rm{t = }}\sqrt {{{2{\rm{MI}}} \over {\rm{a}}}} = \sqrt {{{2.6} \over 3}} = 2{\rm{s}}{\rm{.}}\)
Câu hỏi 27 :
Mức cường độ âm do nguồn S gây ra tại M là L, khi cho S tiến lại gần M một đoạn 62m thì mức cường độ âm thăng thêm 3dB. Khoảng cách từ S đến M là
- A 112m
- B 210m
- C 148m
- D 130m
Đáp án: B
Phương pháp giải:
áp dụng công thức tính mức cường độ âm
Lời giải chi tiết:
Mức cường độ âm tại điểm M:
\({L_M} = \log \frac{{{I_M}}}{{{I_0}}}\)
Mức cường độ âm tại N là:
\({L_N} = \log \frac{{{I_N}}}{{{I_0}}} = {L_M} + 0,3\)
Mặt khác ta có:
\(\begin{gathered}
\frac{{{I_M}}}{{{I_N}}} = \frac{{{{\left( {r - 62} \right)}^2}}}{{{r^2}}} = > {I_N} = {I_M}.\frac{{{r^2}}}{{{{\left( {r - 62} \right)}^2}}} \hfill \\
\log \frac{{{I_N}}}{{{I_0}}} = \log \left( {\frac{{{I_M}}}{{{I_0}}}.\frac{{{r^2}}}{{{{\left( {r - 62} \right)}^2}}}} \right) = \log \frac{{{I_M}}}{{{I_0}}} + \log \frac{{{r^2}}}{{{{\left( {r - 62} \right)}^2}}} = {L_M} + 0,3 \hfill \\
= > \log \frac{{{r^2}}}{{{{\left( {r - 62} \right)}^2}}} = 0,3 \hfill \\
\frac{r}{{r - 62}} = {10^{0,3:2}} = {10^{0,15}} \hfill \\
= > r = 210m \hfill \\
\end{gathered} \)
Câu hỏi 28 :
Một sóng âm truyền trong không khí. Mức cường độ âm tại điểm M và tại điểm N lần lượt là 40dB và 80dB. Cường độ âm tại N lớn hơn cường độ âm tại M
- A 1000 lần
- B 40 lần
- C 2 lần
- D 10000 lần
Đáp án: D
Phương pháp giải:
Mức cường độ âm: \(L = 10.\log {I \over {{I_0}}}(dB)\)
Lời giải chi tiết:
Ta có: \(\left\{ \matrix{
{L_M} = 10.\log {{{I_M}} \over {{I_0}}} = 40 \hfill \cr
{L_N} = 10.\log {{{I_N}} \over {{I_0}}} = 80 \hfill \cr} \right. \Rightarrow {L_N} - {L_M} = 10.\log {{{I_N}} \over {{I_M}}} = 40 \Rightarrow {I_N} = 10000.{I_M}\)
Mức cường độ âm ![]()
Câu hỏi 29 :
Hai điểm A và B nằm trên cùng một đường thẳng đi qua một nguồn âm. Biết mức cường độ âm tại A và tại B chênh nhau là 20 (dB). Coi môi trường không có sự phản xạ và hấp thụ âm. Tỉ số cường độ âm của chúng có thể là
- A 104
- B 2.102
- C 102
- D 2.104
Đáp án: C
Phương pháp giải:
Áp dụng công thức tính mức cường độ âm tại 1 điểm
Lời giải chi tiết:
Đáp án C
Áp dụng côn thức tính mức cường độ âm tại 1 điểm ta có \({L_A} - {L_B} = 10\log {{{I_A}} \over {{I_B}}} = 20 = > {{{I_A}} \over {{I_B}}} = {10^2}\)
Câu hỏi 30 :
Tại O có 1 nguồn âm điểm phát âm thanh đẳng hướng với công suất không đổi. Một người đi bộ từ A đến C theo một đường thẳng và nghe được âm thanh từ nguồn O, thì người đó thấy cường độ âm tăng từ I đến 2I rồi lại giảm xuống I. Khoảng cách AO bằng
- A \({{\sqrt 3 } \over 2}AC.\)
- B \({{AC} \over 3}.\)
- C \({{\sqrt 2 } \over 2}AC.\)
- D \({{AC} \over 2}.\)
Đáp án: C
Lời giải chi tiết:
Đáp án C
+ Cường độ âm tại A và C bằng nhau => OAC cân tại O.
Ta có \(I\~{1 \over {{r^2}}} \to \) với \({I_H} = 2{I_A}\) thì \(OA = \sqrt 2 OH.\)
+ Ta chuẩn hóa \(OA = 1 \to OA = \sqrt 2 .\)
\(AC = 2\sqrt {O{A^2} - O{H^2}} = 2\sqrt {O{A^2} - O{H^2}} = 2\sqrt {{{\left( {\sqrt 2 } \right)}^2} - {1^2}} = 2.\)
\( \to OA = {{\sqrt 2 } \over 2}AC.\)
Câu hỏi 31 :
Hai điểm M và N nằm trên cùng 1 phương truyền âm từ nguồn âm O. Tại M và N có mức cường độ âm lần lượt là LM = 30 dB, LN = 10 dB. Coi nguồn phát âm đẳng hướng và môi trường không hấp thụ âm. Tỉ số OM/ON bằng
- A 1/3.
- B 10
- C 1/10.
- D 1/100.
Đáp án: C
Phương pháp giải:
Áp dụng công thức tính mức cường độ âm, mối liên hệ giữa cường độ âm và khoảng cách đến nguồn âm
Lời giải chi tiết:
ta có
\(\left\{ \begin{array}{l}
{I_M} = {I_0}{.10^3}{\rm{W}}/{m^2}\\
{I_N} = {I_0}{.10^1}{\rm{W}}/{m^2}
\end{array} \right. \Rightarrow \frac{{{I_N}}}{{{I_M}}} = \frac{{O{M^2}}}{{0{N^2}}} = \frac{{10}}{{1000}} = \frac{1}{{100}} \Rightarrow \frac{{OM}}{{ON}} = \frac{1}{{10}}\)
Câu hỏi 32 :
Cho ống sao có một đầu bịt kín và một đầu để hở. Biết rằng ống sáo phát ra âm thanh to nhất ứng với hai tần số của hai họa âm liên tiếp là 150Hz và 250Hz. Tần số âm nhỏ nhất khi ống sao phát ra âm thanh to nhất bằng
- A 50Hz
- B 75Hz
- C 25Hz
- D 100Hz
Đáp án: A
Lời giải chi tiết:
Theo bài ra ta có tần số nhỏ nhất khi ống sáo phát ra âm thanh to nhất bằng \({f_{min}} = {{{f_2} - {f_1}} \over 2} = 50(Hz)\)
Câu hỏi 33 :
Một nguồn âm S có công suất P phát sóng đều mọi phương. Hai điểm A, B nằm trên nửa đường thẳng xuất phát từ S. Mức cường độ âm tại A là 80 dB, tại B là 60dB. Mức cường độ âm tại trung điểm M của AB là
- A 70 dB
- B 72dB
- C 60dB
- D 65dB
Đáp án: D
Phương pháp giải:
Mức cường độ âm: \(L = 10.\log {P \over {4\pi .{R^2}.{I_0}}}\) (R là khoảng cách từ nguồn âm đến điểm khảo sát)
Lời giải chi tiết:
M là trung điểm của AB: \(SM = {{SA + SB} \over 2}\)
Mức cường độ âm tại A và B:
\(\left\{ \matrix{
{L_A} = 10.\log {P \over {4\pi .S{A^2}.{I_0}}} = 80dB \hfill \cr
{L_B} = 10.\log {P \over {4\pi .S{B^2}.{I_0}}} = 60dB \hfill \cr} \right. \Rightarrow {L_A} - {L_B} = 10\log {{S{B^2}} \over {S{A^2}}} = 20 \Rightarrow SB = 10.SA \Rightarrow SM = {{11} \over 2}SA\)
Mức cường độ âm tại M:
\(\eqalign{
& {L_M} = 10.\log {P \over {4\pi .S{M^2}.{I_0}}} = 10.\log {P \over {4\pi .{{\left( {{{11} \over 2}SA} \right)}^2}.{I_0}}} \cr
& \Rightarrow {L_A} - {L_M} = 10.\log {\left( {{{11} \over 2}} \right)^2} \Rightarrow {L_M} = 80 - 10.\log {\left( {{{11} \over 2}} \right)^2} = 65dB \cr} \)
Câu hỏi 34 :
Để đo tốc độ âm trong gang, nhà vật lí Pháp Bi-ô đã dùng một ống bằng gang dài 951,25m. Một người đập một nhát búa vào một đầu ống gang, một người ở đầu kia nghe thấy hai tiếng gõ, một truyền qua gang và một truyền qua không khí trong ống gang; hai tiếng ấy cách nhau 2,5s. Biết tốc độ âm trong không khí là 340 m/s, hãy tính tốc độ âm trong gang.
- A 3294m/s
- B 3000m/s
- C 3194 m/s
- D 3300m/s
Đáp án: C
Phương pháp giải:
Áp dụng điều kiện hai tiếng nghe được cách nhau khoảng thời gian : \(t = \frac{1}{{{v_0}}} - \frac{1}{{{v_g}}}\)
Lời giải chi tiết:
Gọi L là chiều dài của ống gang.
Hai tiếng nghe được cách nhau khoảng thời gian : \(t = \frac{L}{{{v_0}}} - \frac{L}{{{v_g}}}\)
Ta có:
\(\begin{gathered}
t = \frac{L}{{{v_0}}} - \frac{L}{{{v_g}}} \Rightarrow \frac{L}{{{v_g}}} = \frac{L}{{{v_0}}} - t \Leftrightarrow \frac{L}{{{v_g}}} = \frac{{L - {v_0}t}}{{{v_0}}} \hfill \\
\Leftrightarrow {v_0}L = \left( {L - {v_0}t} \right).{v_g} \Rightarrow {v_g} = \frac{{{v_0}L}}{{L - {v_0}t}} \hfill \\
\end{gathered} \)
Tốc độ truyền âm trong gang : \({v_g} = \frac{{{v_0}L}}{{L - {v_0}t}} = \frac{{340.951,25}}{{951,25 - 340.2,5}} \approx 3194m/s.\)
Chọn C.
Câu hỏi 35 :
Nguồn âm S phát ra âm có công suất P = 4π.10-5 W không đổi, truyền đẳng hướng về mọi phương. Cho cường độ âm chuẩn I0 = 10-12 W/m2. Điểm M cách nguồn S một đoạn 1m có mức cường độ âm là
- A 50 dB.
- B 60 dB.
- C 70 dB.
- D 80 dB.
Đáp án: C
Phương pháp giải:
Mức cường độ âm: \(L = 10.\log \frac{P}{{4\pi {r^2}.{I_0}}}\)(r là khoảng cách từ nguồn âm đến điểm khảo sát)
Lời giải chi tiết:
Đáp án C
Mức cường độ âm tại M: \({L_M} = 10.\log \frac{P}{{4\pi {r^2}{I_0}}} = 10.\log \frac{{4\pi {{.10}^{ - 5}}}}{{4\pi {{.1}^2}{{.10}^{ - 12}}}} = 70dB\)
Câu hỏi 36 :
Ba điểm O, A, B cùng nằm trên một nửa đường thẳng xuất phát từ O. Tại O đặt một nguồn điểm phát sóng âm đẳng hướng trong không gian, môi trường không hấp thụ âm. Mức cường độ âm tại A là 60dB, tại B là 20dB. Mức cường độ âm tại trung điểm M của đoạn AB là
- A 40dB
- B 34dB
- C 26dB
- D 17dB
Đáp án: C
Phương pháp giải:
Mức cường độ âm: \(L = 10.\log \frac{P}{{4\pi {r^2}.{I_0}}}\,\,(dB)\) (r là khoảng cách từ nguồn đến điểm khảo sát)
Lời giải chi tiết:
Đáp án C
M là trung điểm của AB \( \Rightarrow OM = \frac{{OA + OB}}{2}\)
Mức cường độ âm tại A, B và M: \(\left\{ \begin{array}{l}{L_A} = 10.\log \frac{P}{{4\pi .O{A^2}.{I_0}}} = 60\\{L_B} = 10.\log \frac{P}{{4\pi .O{B^2}.{I_0}}} = 20\\{L_M} = 10.\log \frac{P}{{4\pi .O{M^2}.{I_0}}}\end{array} \right.\)
Ta có:
\(\begin{array}{l}{L_A} - {L_B} = 40 \Leftrightarrow 10.\log \frac{P}{{4\pi O{A^2}.{I_0}}}\,\, - 10.\log \frac{P}{{4\pi O{B^2}.{I_0}}} \Leftrightarrow 10\log \frac{{O{B^2}}}{{O{A^2}}} = 40 \Rightarrow OB = 100.OA \Rightarrow OM = \frac{{101.OA}}{2}\\ \Rightarrow {L_A} - {L_M} = 10.\log \frac{P}{{4\pi O{A^2}.{I_0}}}\,\, - 10.\log \frac{P}{{4\pi O{M^2}.{I_0}}} = 10.\log \frac{{O{M^2}}}{{O{A^2}}} = 10.\log \frac{{{{\left( {\frac{{101.OA}}{2}} \right)}^2}}}{{O{A^2}}}\\ \Leftrightarrow 60 - {L_M} = 10\log {\left( {\frac{{101}}{2}} \right)^2} \Rightarrow {L_M} = 26dB\end{array}\)
Câu hỏi 37 :
Một nguồn âm có công suất không đổi đặt tại A, truyền theo mọi hướng trong một môi trường không hấp thụ âm. Mức cường độ âm tại hai điểm B và C lần lượt là 50 dB và 48 dB. Biết ba điểm A, B, C tạo thành tam giác vuông tại B và AB = 8 m. Khoảng cách BC gần giá trị nào sau đây?
- A 10 m.
- B 4 m.
- C 16 m.
- D 6 m.
Đáp án: D
Lời giải chi tiết:
Đáp án D
+ Ta có \(\cos A = \frac{{AB}}{{AC}} = {10^{\frac{{{L_C} - {L_B}}}{{20}}}} = {10^{\frac{{48 - 50}}{{20}}}} = {10^{ - 0,1}} = > \alpha \approx {37^0}\)
Ta có BC = ABtan A = 6,11 cm.
Câu hỏi 38 :
Một người đứng cách một bức tường 500 m nghe một tiếng súng nổ. Vị trí đặt súng cách tường 165 m. Người và súng cùng trên đường thẳng vuông góc với tường. Sau khi nghe tiếng nổ, người này lại nghe tiếng nổ do âm thanh phản xạ trên bức tường. Tốc độ âm thanh trong không khí là 330 m/s. Khoảng thời gian giữa hai tiếng nổ là:
- A $\frac{1}{3}s$
- B $\frac{2}{3}s$
- C 1s
- D $\frac{4}{3}s$
Đáp án: C
Phương pháp giải:
Phương pháp: Sử dụng công thức $S{\text{ }} = {\text{ }}v.t$
Lời giải chi tiết:
Đáp án C
Lời giải:
Khoảng cách giữa người và súng là: $L\; = {\text{ }}500{\text{ }} - {\text{ }}165{\text{ }} = {\text{ }}335m$
Gọi t1 là thời gian lúc súng bắt đầu nổ đến tai người: ${t_1} = \frac{{{S_1}}}{v} = \frac{{335}}{v}$
t2 là thời gian do âm thanh phản xạ trên bức tường sau khi nghe tiếng nổ: ${t_2} = \frac{{{S_2}}}{v} = \frac{{500 + 165}}{v}$
Thời gian giữa hai lần tiếng nổ đến tai người là: $\Delta t = {t_2} - {t_1} = \frac{{500 + 165}}{v} - \frac{{335}}{v} = \frac{{330}}{v} = \frac{{330}}{{330}} = 1{\text{s}}$
=> Chọn C
Câu hỏi 39 :
Có một số nguồn âm giống nhau với công suất phát âm không đổi trong môi trường đẳng hướng không hấp thụ âm. Nếu tại điểm A đặt 4 nguồn âm thì tại điểm B cách A một đoạn d có mức cường độ âm là 60dB. Nếu tại điểm C cách B một đoạn 2d/3 đặt 6 nguồn âm thì tại điểm B có mức cường độ âm bằng
- A 58,42dB
- B 65,28dB
- C 54,72dB
- D 61,76dB
Đáp án: B
Phương pháp giải:
Phương pháp: Áp dụng công thức tính cường độ âm $I = \frac{P}{{4\pi {R^2}}}$
Lời giải chi tiết:
Đáp án B
Lời giải:
Gọi công suất mỗi nguồi là P
Cường độ âm tại B do A gây ra: ${I_{AB}} = \frac{{4P}}{{4\pi {d^2}}} = {10^{ - 6}}W/{m^2}$
Cường độ âm tại B do C gây ra: ${I_{CB}} = \frac{{6P}}{{4\pi {{(\frac{{2d}}{3})}^2}}} = \frac{{4P}}{{4\pi {d^2}}}\frac{{27}}{8} = 3,{375.10^{ - 6}}W/{m^2}$
$ \to {L_B} = \log \frac{{{I_{CB}}}}{{{{10}^{ - 12}}}} = 6,528B = 65,28dB$
=> Chọn B
Câu hỏi 40 :
Trong buổi hòa nhạc được tổ chức ở Nhà hát Lớn Hà Nội nhân dịp kỉ niệm 1000 năm Thăng Long. Một người ngồi dưới khán đài nghe được âm do một chiếc đàn giao hưởng phát ra có mức cường độ 68 dB. Khi dàn nhạc giao hưởng thực hiện bản hợp xướng người đó cảm nhận được âm là 80dB. Hỏi dàn nhạc giao hưởng đó có bao nhiêu người?
- A 18 người.
- B 12 người.
- C 16 người.
- D 8 người
Đáp án: C
Phương pháp giải:
Sử dụng công thức tính mức cường độ âm và cường độ âm
Lời giải chi tiết:
Cường độ âm tỉ lệ thuận với công suất của nguồn phát âm
Độ to của âm lại phụ thuộc vào mức cường độ âm.
Gọi mức cường độ âm khi đàn và khi cả dàn nhạc hợp xướng lần lượt là L1 và L2. Ta có:
\(\begin{array}{l}
{L_1} = 68dB = 10\log \left( {\frac{{{I_1}}}{{{I_0}}}} \right)\\
{L_2} = 80dB = 10\log \left( {\frac{{{I_2}}}{{{I_0}}}} \right)\\
= > {L_2} - {L_1} = 80 - 68 = 10\log \left( {\frac{{{I_2}}}{{{I_0}}}} \right) - 10\log \left( {\frac{{{I_1}}}{{{I_0}}}} \right) = 10\log \left( {\frac{{{I_2}}}{{{I_1}}}} \right) = 10\log \frac{{{P_2}}}{{{P_1}}}\\
= > \frac{{{P_2}}}{{{P_1}}} = {10^{1,2}} = 15,85\\
= > {P_2} = 15,84{P_1}
\end{array}\)
Câu hỏi 41 :
Một dây đàn dài 15cm, khi gãy phát ra âm cơ bản với tốc độ truyền sóng trên dây là 300m/s. Tốc độ truyền âm trong không khí là 340m/s. Bước sóng của âm phát ra trong không khí là:
- A 0,5m
- B 1,24m
- C 0,34m
- D 0,68m
Đáp án: C
Phương pháp giải:
Phương pháp:
+ Sử dụng công thức chiều dài dây đàn: $l = k\frac{\lambda }{2}$
+ Sử dụng công thức tính bước sóng: $\lambda = \frac{v}{f}$
Lời giải chi tiết:
Đáp án C
Lời giải:
$l = k\frac{\lambda }{2} = k\frac{v}{{2f}} \to f = k\frac{v}{{2l}}$
Tần số của âm cơ bản: ${f_1} = \frac{v}{{2l}} = \frac{{300}}{{2.0,15}} = 1000H{\text{z}}$
Bước sóng của âm phát ra trong không khí: $\lambda = \frac{{{v_{kk}}}}{{{f_1}}} = \frac{{340}}{{1000}} = 0,34m$
=> Chọn C
Câu hỏi 42 :
Một nguồn âm điểm đặt tại O phát âm đẳng hướng với công suất không đổi trong một môi trường không hấp thụ và phản xạ âm. Hai điểm M và N cách O lần lượt là r và r - 50 (m) có cường độ âm tương ứng là I và 4I. Giá trị của r bằng
- A 60 m
- B 66 m
- C 100m
- D 142 m
Đáp án: C
Lời giải chi tiết:
Đáp án C
Phương pháp : Công thức tính cường độ âm
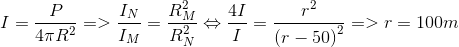
Câu hỏi 43 :
Trong một bản hợp ca, giả sử mọi ca sĩ đều hát với cùng một cường độ âm và cùng tần số. Khi một ca sĩ hát thì mức cường độ âm tại một điểm M là 68 dB. Khi cả ban hợp ca cùng hát thì đo được mức cường độ âm là 80 dB. Số ca sĩ có trong bản hợp ca là
- A 18 người.
- B 12 người.
- C 16 người.
- D 19 người.
Đáp án: C
Phương pháp giải:
Sử dụng công thức tính mức cường độ âm
Lời giải chi tiết:
Khi có 1 ca sĩ hát thì cường độ âm tại điểm M là I và mức cường độ âm là 68dB, ta có
\({L_M} = 10\lg {I \over {{I_0}}} = 68dB\)
Khi cả ban hợp ca gồm n ca sĩ hát thì cường độ âm tại M là nI và mức cường độ âm là L’M, ta có
\(L{'_M} = 10\lg {{nI} \over {{I_0}}} = 10\lg {I \over {{I_0}}} + 10\lg n = 80dB\)
\( \Rightarrow 10\lg n = 80 - 10\lg {I \over {{I_0}}} = 80 - 68 = 12 \Rightarrow n \approx 16\)
=> Chọn đáp án C
Câu hỏi 44 :
Đặt nguồn âm điểm phát đẳng hướng trong môi trường truyền âm đồng tính không hấp thụ âm. Di chuyển một thiết bị đo mức cường độ âm dọc theo một đường thẳng trong môi trường đó thì thấy mức cường độ âm tại vị trí ban đầu có giá trị 40 dB, tăng dần đến giá trị cực đại bằng 60 dB rồi giảm dần và có mức cường độ âm là 50 dB tại vị trí dừng lại. Biết quãng đường di chuyển của thiết bị đo là 60 m. Khoảng cách ngắn nhất giữa thiết bị đo với nguồn phát âm gần nhất với giá trị nào sau đây
- A 3 m.
- B 6,5 m.
- C 38 m.
- D 40 m.
Đáp án: A
Phương pháp giải:
Áp dụng công thức tính mức cường độ âm \(L=10.\log \frac{I}{{{I}_{o}}}\)(dB)
Lời giải chi tiết:
+\(\underbrace {{L_H} - {L_M}}_{20(dB)} = 20\log \frac{{SM}}{{SH}} \to SM = 10SH\);
+\(\underbrace {{L_H} - {L_N}}_{10(dB)} = 20\log \frac{{SN}}{{SH}} \to SN = \sqrt {10} SH\)
\( \to MH + HN = \underbrace {\sqrt {S{M^2} - S{H^2}} }_{SH\sqrt {99} } + \underbrace {\sqrt {S{N^2} - S{H^2}} }_{SH.3} = 60\)
=> \(SH\approx \)\(4,633(cm)\)
Chọn A
Câu hỏi 45 :
Bạn An chợt tỉnh ngủ vì tiếng vo ve bên tai gây ra bởi một con muỗi. Số lần đập cánh của con muỗi trong một phút có thể là
- A 1200 lần
- B 900 lần
- C 600 lần
- D 500 lần
Đáp án: A
Phương pháp giải:
Tai người có thể nghe được âm có tần số khoảng từ 20 Hz - 20000 Hz
Lời giải chi tiết:
An nghe được tiếng muỗi nên số lần đập cánh của con muỗi trong một giây phải không nhỏ hơn 20, tức số lần đập cánh của con muỗi trong một phút phải từ 20.60 = 1200 lần trở lên.
Câu hỏi 46 :
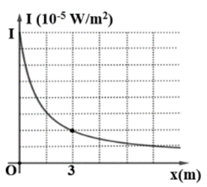
Tại một điểm trên trục Ox có một nguồn âm điểm phát âm đẳng hướng ra môi trường. Hình bên là đồ thị biểu diễn sự phụ thuộc của cường độ âm I tại những điểm trên trục Ox theo tọa độ x. Nếu tại cường độ âm tại O là I thì cường độ âm tại điểm P có tọa độ \({{x}_{p}}\text{= }5m\) cường độ âm có giá trị Ip . Tỉ số \(\frac{{{I}_{P}}}{I}\) gần nhất với giá trị nào dưới đây?
- A 0,36.
- B 0,20.
- C 0,25.
- D 0,14.
Đáp án: D
Phương pháp giải:
Áp dụng công thức tính công suất tính công suất tính mức cường độ âm
Lời giải chi tiết:
Theo bài ra ta có \(\frac{8}{2}={{\left( \frac{SO+3}{SO} \right)}^{2}}=>SO=3m\)
Tương tự ra có \(\frac{{{I}_{P}}}{{{I}_{I}}}={{\left( \frac{SO}{SO+5} \right)}^{2}}\Leftrightarrow \frac{I}{{{I}_{P}}}={{\left( \frac{3}{3+5} \right)}^{2}}=0,14\)
Chọn D
Câu hỏi 47 :
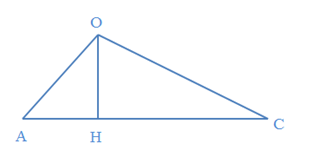
Đặt nguồn âm điểm tại O với công suất không đổi, phát sóng âm đẳng hướng trong môi trường không hấp thụ âm. Một máy đo cường độ âm di chuyển từ A đến C theo một đường thẳng, cường độ âm thu được tăng từ 30µW/m2 đến 40µW/m2, sau đó giảm dần xuống 10µW/m2. Biết OA = 36 cm. Quãng đường mà máy thu đã di chuyển có giá trị gần nhất với giá trị nào sau đây?
- A 140cm
- B 35cm
- C 70cm
- D 105cm
Đáp án: C
Phương pháp giải:
Nguồn công suất P gây ra tại điểm cách nó đoạn d cường độ âm là \(I=\frac{P}{4\pi {{d}^{2}}}\)
Lời giải chi tiết:
Nguồn công suất P gây ra tại điểm cách nó đoạn d cường độ âm là \(I=\frac{P}{4\pi {{d}^{2}}}\)
Ta có:
\(\frac{{{I}_{A}}}{{{I}_{H}}}=\frac{O{{H}^{2}}}{O{{A}^{2}}}=\frac{3}{4}\Rightarrow O{{H}^{2}}=\frac{3}{4}O{{A}^{2}}=972c{{m}^{2}}\)
\(\frac{{{I}_{C}}}{{{I}_{A}}}=\frac{O{{A}^{2}}}{O{{C}^{2}}}=\frac{1}{3}\Rightarrow O{{C}^{2}}=3O{{A}^{2}}=3888c{{m}^{2}}\)
Từ hình vẽ ta có khoảng cách AC là :
\(AC=AH+HC=\sqrt{O{{A}^{2}}-O{{H}^{2}}}+\sqrt{O{{C}^{2}}-O{{H}^{2}}}=\sqrt{{{36}^{2}}-972}+\sqrt{3888-972}=72m\)
Chọn C
Câu hỏi 48 :
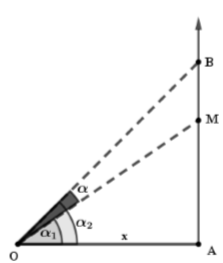
Tại điểm O đặt hai nguồn âm điểm giống hệt nhau phát ra âm đẳng hướng có công suất không đổi. Điểm A cách O một đoạn x (m). Trên tia vuông góc với OA tại A lấy điểm B cách A một khoảng 6 m. Điểm M thuộc đoạn AB sao cho AM = 4,5 m. Thay đổi x để góc MOB có giá trị lớn nhất, khi đó mức cường độ âm tại A là LA = 40 dB. Để mức cường độ âm tại M là 50 dB thì cần đặt thêm tại O bao nhiêu nguồn âm nữa?
- A 33
- B 35
- C 15
- D 25
Đáp án: A
Phương pháp giải:
Áp dụng công thức tính mức cường độ âm \(L=10\lg \frac{I}{{{I}_{0}}}\)
Lời giải chi tiết:
Từ hình vẽ ta có
\(\eqalign{
& \alpha = MOB = {\alpha _2} - {\alpha _1} \Leftrightarrow \tan \alpha = {{\tan {\alpha _2} - \tan {\alpha _1}} \over {1 + \tan {\alpha _2}.\tan {\alpha _1}}} = {{{{AB} \over x} - {{AM} \over x}} \over {1 + {{AB} \over x}.{{AM} \over x}}} \cr
& \Leftrightarrow \tan \alpha = {{{6 \over x} - {{4,} \over x}} \over {1 + {{6.4,5} \over {{x^2}}}}} = {{1,5} \over {x + {{27} \over x}}} = > {\alpha _{max}} \Leftrightarrow x = \sqrt {27} m = > \left\{ \matrix{
OB = 3\sqrt 7 m \hfill \cr
OM = 6,87m \hfill \cr} \right. \cr} \)
Khi tại O có 2 nguồn âm \(\frac{{{I}_{A}}}{{{I}_{M}}}={{\left( \frac{OM}{OA} \right)}^{2}}={{10}^{\frac{{{L}_{A}}-{{L}_{M}}}{10}}}\Leftrightarrow {{\left( \frac{6,87}{\sqrt{27}} \right)}^{2}}={{10}^{\frac{40-{{L}_{M}}}{10}}}=>{{L}_{M}}=37,57dB\)
Khi taijO có n nguồn âm và L’M = 50 dB
Ta có \(\frac{I{{'}_{M}}}{{{I}_{M}}}=\frac{n}{2}={{10}^{\frac{L{{'}_{M}}-{{L}_{M}}}{10}}}=\frac{n}{2}\Leftrightarrow \frac{n}{10}={{10}^{\frac{50-37,57}{10}}}\Leftrightarrow n=35\)
Vậy só nguồn âm cần đặt thêm tại O là 35 -2 – 33 ( nguồn)
Chọn A
Câu hỏi 49 :
Tại điểm O trong môi trường đẳng hướng không hấp thụ âm, có 9 nguồn âm điểm giống nhau, công suất phát âm không đổi. Trong môi trường đó tại điểm A có mức cường độ âm là 20 dB. M là điểm thuộc OA sao cho OM= OA/3. Để mức cường độ âm ở M là 30 dB thì số nguồn âm giống các nguồn trên cần đặt ở O là
- A 30
- B 10
- C 27
- D 3
Đáp án: B
Phương pháp giải:
Nguồn công suất P gây ra tại điểm M cách nó đoạn d cường độ âm là \(I=\frac{P}{4\pi {{d}^{2}}}\)
Tại M có mức cường độ âm là L (B) thì có cường độ âm là I = I0.10L
Lời giải chi tiết:
Cường độ âm tại A là: \({{I}_{A}}=\frac{9P}{4\pi .O{{A}^{2}}}={{I}_{0}}{{.10}^{2}}\) (1)
Để tại M có mức cường độ âm 30dB thì cần đặt tại O n nguồn âm
Cường độ âm tại M là : \({{I}_{M}}=\frac{nP}{4\pi .O{{M}^{2}}}={{I}_{0}}{{.10}^{3}}\)(2)
Chia vế cho vế của (1) và (2) ta được : \(\frac{n.O{{A}^{2}}}{O{{M}^{2}}.9}=10\Rightarrow n=10\)
Vậy cần đặt 10 nguồn âm ở O để tại M có mức cường độ âm 30dB
Chọn B
Câu hỏi 50 :
Tại vị trí O trong một nhà máy, một còi báo cháy (xem là nguồn điểm) phát âm với công suất không đổi. Từ bên ngoài, một thiết bị xác định mức cường độ âm chuyển động thẳng từ M hướng đến O theo hai giai đoạn với gia tốc có cùng độ lớn 0,4 m/s2, vận tốc ban đầu bằng không và đến N thì thiết bị đừng lại (cổng nhà máy). Biết NO = 10 m và mức cường độ âm (do còi phát ra) tại N lớn hơn mức cường độ âm tại M là 20 dB. Cho rằng môi trường truyền âm đẳng hướng và không hấp thụ âm. Thời gian thiết bị đó chuyển động từ M đến N có giá trị gần giá trị nào nhất sau đây?
- A 27 s.
- B 47 s.
- C 32 s.
- D 25 s.
Đáp án: C
Phương pháp giải:
- Áp dụng công thức về mức cường độ âm
\(L = \log \frac{I}{{{I_0}}}\), và biết rằng cường độ âm tỉ lệ nghịch với bình phương khoảng cách từ nguồn âm đến vị trí mà ta xét.
- Công thức tính thời gian trong chuyển động biến đổi đều
\(s = \frac{1}{2}.a.{t^2} \Rightarrow t = \sqrt {\frac{{2s}}{a}} \)
Lời giải chi tiết:
Vì mức cường độ âm tại N lớn hơn mức cường độ âm tại M nên ta có:
\(\begin{array}{l}
{L_N} - {L_M} = 20 = 10\log \frac{{{I_N}}}{{{I_M}}} = 10\log \frac{{r_M^2}}{{r_N^2}} = 20\log \frac{{{r_M}}}{{{r_N}}}\\
\Rightarrow \log \frac{{{r_M}}}{{{r_N}}} = 1 \Leftrightarrow {r_M} = 10{r_N} = 100m\\
ON = 10m;OM = 100m \Rightarrow MN = 90m
\end{array}\)
Chuyển động của thiết bị trên đoạn MN chia làm 2 giai đoạn, giai đoạn đầu chuyển động nhanh dần đều đến trung điểm của MN, giai đoạn sau chuyển động chậm dần đều.
Thời gian chuyển động của thiết bị là
\(t = 2\sqrt {\frac{{2MI}}{a}} = 2.\sqrt {\frac{{90}}{{0,4}}} = 30s\)
Vậy đáp án gần nhất là 32s.