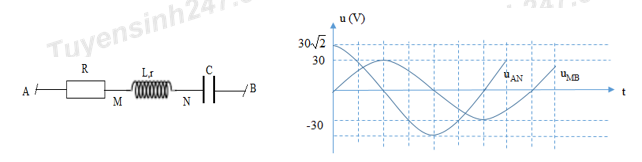Câu hỏi 1 :
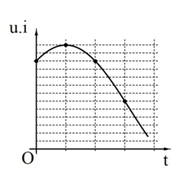
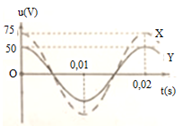
Một đoạn mạch X gồm các phần tử điện trở R, cuộn dây thuần cảm L, tụ điện C mắc nối tiếp. Mắc nối tiếp đoạn mạch X với đoạn mạch Y gồm điện trở thuần và cuộn thuần cảm có độ tự cảm mắc nối tiếp. Mắc vào hai đầu đoạn mạch chứa X và Y một điện áp xoay chiều không đổi thì đồ thị điện áp tức thời (dạng hình sin) của đoạn mạch X đường nét đứt và đoạn mạch Y đường nét liền như trên hình vẽ. Nếu thay đoạn mạch Y bằng đoạn mạch Z gồm cuộn dây không thuần cảm có nối tiếp với tụ điện thì hệ số công suất của đoạn mạch Z là 0,5 (biết hộp Z có tính dung kháng). Công suất tiêu thụ của đoạn mạch lúc này gần giá trị nào nhất sau đây?
- A 90W
- B 100W
- C 120W
- D 110W
Đáp án: B
Phương pháp giải:
Phương pháp đọc đồ thị và vận dụng các công thức điện xoay chiều.
Lời giải chi tiết:
Đáp án B
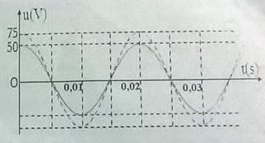
Từ đồ thị ta có: $$T = 0,02s \to \omega = 100\pi {\rm{ }}ra{\rm{d/s}}$$, uX và uY cùng pha.
Mạch lúc này có tính cảm kháng (ZL(X)>ZC(X))
U0=U0X+U0Y=50+75=125
Khi thay mạch Y bằng mạch Z (có tính dung kháng):
$$\eqalign{ & {\rm{cos}}{\varphi _Z} = {r \over {{Z_Z}}} = {r \over {\sqrt {{r^2} + {{({Z_{L(Z)}} - {Z_{C(Z)}})}^2}} }} = 0,5 \cr & \to 3{{\rm{r}}^2} = {({Z_{L(Z)}} - {Z_{C(Z)}})^2} \to {Z_{C(Z)}} - {Z_{L(Z)}} = {Z_{LC(Z)}} = \sqrt 3 r = 60\Omega \cr} $$
Ta có:
$$\eqalign{ & {Z_{LC(X)}} = {Z_{CL(Y)}} = 60\Omega \leftrightarrow {Z_{L(X)}} - {Z_{C(X)}} = {Z_{C(Z)}} - {Z_{L(Z)}} \cr & \leftrightarrow \sum {{Z_L} = \sum {{Z_C}} } \cr} $$
=> Mạch X mắc nối tiếp với Z có cộng hưởng, khi đó: Công suất tiêu thụ của mạch $${P_{{\rm{max}}}} = {{{U^2}} \over {R + r}} = {{{{U_0^2} \over 2}} \over {R + r}} = {{{{125}^2}} \over {2(45 + 20\sqrt 3 )}} = 98,1W$$
=> chọn B
Câu hỏi 2 :
Cho một mạch điện gồm biến trở Rx mắc nối tiếp với tụ điện có \(C = 63,8\mu F\) và một cuộn dây có điện trở thuần r = 70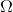 , độ tự cảm \(L = {1 \over \pi }H\). Đặt vào hai đầu một điện áp U = 200V có tần số f = 50Hz. Giá trị của Rx để công suất của mạch cực đại và giá trị cực đại đó lần lượt là:
, độ tự cảm \(L = {1 \over \pi }H\). Đặt vào hai đầu một điện áp U = 200V có tần số f = 50Hz. Giá trị của Rx để công suất của mạch cực đại và giá trị cực đại đó lần lượt là:
- A 0Ω; 378,4W
- B 20Ω; 378,4W
- C 10Ω; 78,4W
- D 30Ω; 100W
Đáp án: A
Phương pháp giải:
Mạch điện có R thay đổi để công suất đạt cực đại
Lời giải chi tiết:
Ta có: ZC = 50Ω; ZL = 100Ω; r = 70Ω
Công suất của mạch đạt cực đại khi:
\(\left\{ \matrix{ {R_x} + r = \left| {{Z_L} - {Z_C}} \right| \hfill \cr {P_{m{\rm{ax}}}} = {{{U^2}} \over {2\left| {{Z_L} - {Z_C}} \right|}} \hfill \cr} \right.\)
Lại có: |ZL – ZC| = 50Ω; r = 70Ω
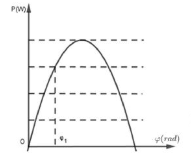
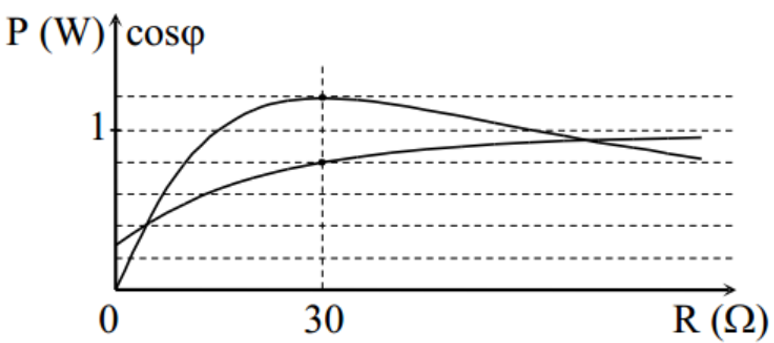
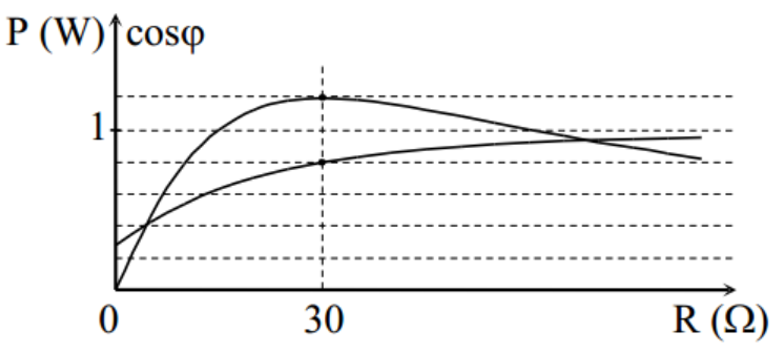
Dựa vào đồ thị biểu diễn sự phụ thuộc của công suất vào (R + r) ta thấy |ZL – ZC| < R + r
=> Pmax <=> Rx + r = 70 => Rx = 0Ω => Pmax = I2.r
\(Z = \sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = 10\sqrt {74} \Omega \Rightarrow I = {{200} \over {10\sqrt {74} }} = {{20} \over {\sqrt {74} }} \Rightarrow {P_{m{\rm{ax}}}} = {\left( {{{20} \over {\sqrt {74} }}} \right)^2}.70 = 378,4W\)
Chọn A
Câu hỏi 3 :
Đoạn mạch nối tiếp theo thứ tự gồm điện trở R, tụ điện có điện dung C và cuộn dây không thuần cảm có độ tự cảm L và điện trở r. Biết L = CR2 = Cr2. Đặt vào đoạn mạch điện áp xoay chiều u = U√2cosωt (V) (có U và ω không đổi) thì điện áp hiệu dụng của đoạn mạch RC gấp √3 lần điện áp hiệu dụng hai đầu dây. Hệ số công suất của đoạn mạch là:
- A 0,657
- B 0,5
- C 0,785
- D 0,866
Đáp án: D
Phương pháp giải:
Hệ số công suất cosφ = (R + r)/Z
Lời giải chi tiết:
Ta có:
\(L = C{R^2} = C{r^2} \Rightarrow \left\{ \matrix{
R = r \hfill \cr
{L \over C} = {R^2} \Rightarrow {Z_L}.{Z_C} = {R^2} \hfill \cr} \right.\)
Có:
\(\eqalign{
& {U_{RC}} = \sqrt 3 {Z_d} \Leftrightarrow {Z_{RC}} = \sqrt 3 {Z_d} \Leftrightarrow {R^2} + Z_C^2 = 3\left( {{r^2} + Z_L^2} \right) \Leftrightarrow Z_C^2 = 2{R^2} + 3Z_L^2 \cr
& \Leftrightarrow Z_L^2 + 2.{Z_L}{Z_C} + Z_C^2 = 2Z_C^2 - 2Z_L^2 \Rightarrow {Z_L} = 3{Z_C} \cr} \)
Thay ZL = 3ZC vào biểu thức ZL.ZC = R2 ta được:
\({Z_C} = {R \over {\sqrt 3 }} \Rightarrow {Z_L} = \sqrt 3 R \Rightarrow Z = \sqrt {{{\left( {2R} \right)}^2} + {{\left( {\sqrt 3 - {1 \over {\sqrt 3 }}} \right)}^2}.{R^2}} = {{4R} \over {\sqrt 3 }} \Rightarrow c{\rm{os}}\varphi = {{R + r} \over Z} = 0,866\)
Chọn D
Câu hỏi 4 :
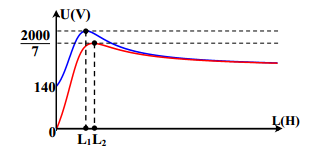
Cho mạch điện xoay chiều gồm điện trở thuần R, tụ điện có điện dung C và cuộn dây có độ tự cảm L mắc nối tiếp theo thứ tự đó. Biết tụ điện có điện dung C có thể thay đổi được, điện áp hai đầu mạch thì mạch tiêu thụ công suất cực đại Pmax= 93,75 W. Khi thì điện áp hiệu dụng trên hai đầu đoạn mạch chứa điện trở thuần và tụ điện (uRC) và cuộn dây (ud) vuông pha với nhau, điện áp hiệu dụng hai đầu cuộn dây khi đó là:
- A 75V.
- B 120V.
- C 90V.
- D (/75\sqrt 2 V\)
Đáp án: B
Phương pháp giải:
Sử dụng công thức tính công suất và giản đồ vecto
Lời giải chi tiết:
Ta có
\(u = 150\sqrt 2 .\cos (100\pi t)V\) => ω = 100π
Khi C = C1= \(frac{{62,5}}{\pi }\mu F\) thì Pmax = 93,75W
\({Z_{{C_1}}} = \frac{1}{{\omega {C_1}}} = 160\Omega \)
Pmax khi Imax ó xảy ra cộng hưởng => \({Z_L} = {Z_C} = 160\Omega \)
\(P = {I^2}R = \frac{{{U^2}}}{{{Z^2}}}.R = \frac{{{U^2}.{R_m}}}{{{R_m}^2 + {{({Z_L} - {Z_C})}^2}}}\)
Thay số từ đề bài P = 93,75W; U = 150; ta tính được Rm = 240Ω
\(C = {C_2} = \frac{1}{{9\pi }} = > {Z_{{C_2}}} = 90\Omega \)
thì Ud vuông pha với URC
Ud vuông pha với URC cho ta biết cuộn dây có điện trở trong r.
\(I = \frac{U}{Z} = \frac{U}{{\sqrt {{R^2} + ({Z_L} - {Z_{{C_2}}})} }} = \frac{{150}}{{\sqrt {{{240}^2} + {{(160 - 90)}^2}} }} = 0,6A\)
Vì ULr vuông góc với URC nên:
\(begin{array}{l}
U_{Lr}^2 + U_{RC}^2 = {150^2}\\
U_L^2 + U_r^2 + U_R^2 + U_C^2 = {150^2}
\end{array}\)
Mặt khác theo định luật Ôm ta có:
\(begin{array}{l}
U_{Rr}^2 + {(U_L^{} - {U_C})^2} = {U^2} = {150^2}\\
{({U_R} + {U_r})^2} + {({U_L} - {U_C})^2} = {150^2}\\
U_{_R}^2 + 2{U_R}{U_r} + U_r^2 + U_L^2 + U_L^2 - 2.{U_L}.{U_C} = {150^2}\\
{U_R}.{U_r} - {U_L}{U_C} = 0\\
= > r.R - {Z_L}.{Z_C} = 0\\
= > r.R = {Z_L}.{Z_C} = 160.90
\end{array}\)
\(left\{ \begin{array}{l}
r.R = 160.90\\
r + R = 240
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
r = 120\Omega \\
R = 120\Omega
\end{array} \right.\)
\({U_d} = I.\sqrt {{r^2} + Z_L^2} = 0,6.\sqrt {{{120}^2} + {{160}^2}} = 120V\)
Câu hỏi 5 :
Đặt điện áp xoay chiều có giá trị hiệu dụng không đổi vào hai đầu đoạn mạch gồm biến trở R mắc nối tiếp với tụ điện. Dung kháng của tụ điện là 100Ω. Khi điều chỉnh R thì tại hai giá trị R1 và R2, công suất tiêu thụ của đoạn mạch là như nhau. Biết điện áp hiệu dụng giữa hai đầu tụ điện khi R = R1 bằng hai lần điện áp hiệu dụng giữa hai đầu tụ điện khi R = R2. Các giá trị R1 và R2 là:
- A R1= 50Ω, R2 = 100Ω.
- B R1= 50Ω, R2 = 200Ω
- C R1= 25Ω, R2 = 100Ω
- D R1= 40Ω, R2 = 250Ω
Đáp án: B
Phương pháp giải:
sử dụng công thức tính công suất
Mạch điện R, L, C mắc nối tiếp có R thay đổi
Lời giải chi tiết:
ZC = 100Ω
Khi P1 = P2 ta có:
\({{{U^2}{R_1}} \over {R_1^2 + {Z_C}^2}} = {{{U^2}{R_2}} \over {R_2^2 + {Z_C}^2}} \Leftrightarrow {R_1}.(R_2^2 + {Z_C}^2) = {R_2}.(R_1^2 + {Z_C}^2) \Leftrightarrow {R_1}{R_2}({R_2} - {R_1}) = {Z_C}^2.({R_2} - {R_1}) \Rightarrow {R_1}{R_2} = {Z_C}^2 = {100^2}(*)\)
mà :
\(\eqalign{
& {U_{C\left( {{R_1}} \right)}} = 2{U_{C\left( {{R_2}} \right)}} \Leftrightarrow {{U{Z_C}} \over {\sqrt {R_1^2 + Z_C^2} }} = {{U{Z_C}} \over {\sqrt {R_2^2 + Z_C^2} }} \Leftrightarrow \sqrt {R_1^2 + Z_C^2} = {1 \over 2}\sqrt {R_2^2 + Z_C^2} \Leftrightarrow R_1^2 + Z_C^2 = {1 \over 4}(R_2^2 + Z_C^2) \cr
& \Leftrightarrow R_1^2 - {1 \over 4}R_2^2 = - {3 \over 4}Z_C^2 = - {3 \over 4}{.100^2}(**) \cr} \)
Rút R1 từ phương trình * thế vào phương trình **
Ta được:
\(R_1^2 - {1 \over 4}.{({{{{100}^2}} \over {{R_1}}})^2} = - {3 \over 4}{.100^2} \Leftrightarrow R_1^4 + {3 \over 4}{.100^2}.R_1^2 - {1 \over 4}{.100^4} = 0 \Leftrightarrow R_1^2 = 2500 \Rightarrow {R_1} = 50\Omega \Rightarrow {R_2} = {{{{100}^2}} \over 4} = 200\Omega \)
Câu hỏi 6 :
Đặt một điện áp xoay chiều \(u = U\sqrt 2 c{\rm{os}}\omega t(V)\), trong đó U không đổi, ω thay đổi được vào một đoạn mạch gồm có điện trở R, tụ điện và cuộn cảm thuần có hệ số tự cảm \(L = {{1,6} \over \pi }H\) mắc nối tiếp. Khi ω = ω0 thì công suất trên đoạn mạch đạt cực đại và bằng 732W. Khi ω = ω1 hoặc ω = ω2 thì công suất tiêu thụ trên đoạn mạch bằng nhau và bằng 300W. Biết ω1 - ω2 = 120π (rad/s). Giá trị của R bằng
- A 240 Ω
- B 133,3 Ω
- C 160 Ω
- D 400 Ω
Đáp án: C
Phương pháp giải:
Mạch điện R, L, C mắc nối tiếp có ω thay đổi
Lời giải chi tiết:
+ Khi ω = ω0 công suất trên mạch đạt cực đại:
\( \Rightarrow \left\{ \matrix{
\omega _0^2 = {1 \over {LC}} \hfill \cr
{P_{m{\rm{ax}}}} = {{{U^2}} \over R} = 732 \Rightarrow {U^2} = 732R(*) \hfill \cr} \right.\)
+ Khi ω = ω1 và ω = ω2 ; ω1 – ω2 = 120π thì công suất tiêu thụ trên đoạn mạch bằng nhau :
\({P_1} = {P_2} = P = 300{\rm{W}} \Leftrightarrow {{{U^2}R} \over {{R^2} + {{\left( {{Z_{L1}} - {Z_{C1}}} \right)}^2}}} = {{{U^2}R} \over {{R^2} + {{\left( {{Z_{L2}} - {Z_{C2}}} \right)}^2}}} \Rightarrow {\omega _1}{\omega _2} = {1 \over {LC}} = \omega _0^2\)
+ Ta có :
\(\eqalign{
& {Z_{L1}} - {Z_{C1}} = {\omega _1}L - {1 \over {{\omega _1}{C_1}}} = {\omega _1}L - {1 \over {{{\omega _0^2} \over {{\omega _2}}}C}} = {\omega _1}L - {{{\omega _2}} \over {\omega _0^2C}} = {\omega _1}L - {{{\omega _2}} \over {{1 \over {LC}}C}} = {\omega _1}L - {\omega _2}L = \left( {{\omega _1} - {\omega _2}} \right)L = 120\pi {{1,6} \over \pi } = 192 \cr
& \Rightarrow {Z_{L1}} - {Z_{C1}} = 192(**) \cr} \)
+ Công suất tiêu thụ : \(P = {{{U^2}R} \over {{R^2} + {{\left( {{Z_{L1}} - {Z_{C1}}} \right)}^2}}} = 300 \Rightarrow 300{R^2} + 300{\left( {{Z_{L1}} - {Z_{C1}}} \right)^2} = {U^2}R(***)\)
Từ (*) ; (**) ; (***) \( \Rightarrow 300{R^2} + {300.192^2} = 732{R^2} \Rightarrow R = 160\Omega \)
Câu hỏi 7 :
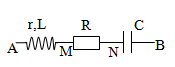
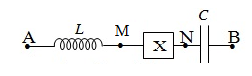
Đoạn mạch A, B được mắc nối tiếp theo thứ tư, cuộn dây với hệ số tự cảm \(L = {2 \over {5\pi }}H\), biến trở R và tụ điện có điện dung \(C = {{{{10}^{ - 2}}} \over {25\pi }}F\). Điểm M là điểm nối giữa R và C. Nếu mắc vào hai đầu A, M một ắc quy có suất điện động 12V và điện trở trong 4Ω điều chỉnh R = R1 thì có dòng điện cường độ 0,1875A. Mắc vào A, B một hiệu điện thế \(u = 120\sqrt 2 c{\rm{os}}\left( {100\pi t} \right)\left( V \right)\) rồi điều chỉnh R = R2 thì công suất tiêu thụ trên biến trở đạt cực đại bằng 160W. Tỷ số R1 : R2 là
- A 1,6
- B 0,25
- C 0,125
- D 0,45
Đáp án: A
Phương pháp giải:
Sử dụng hệ thức của định luật Ôm và công thức tính công suất tiêu thụ
Lời giải chi tiết:
Giả sử cuộn dây thuần cảm:
Ta có, khi R = R2 công suất tiêu thụ trên biến trở cực đại.
Khi đó ta có: R2 = |ZL - ZC | = 40 - 25 = 15W
Mặt khác: \({P_{{R_2}}} = {{{U^2}} \over {2{R_2}}} = {{{{120}^2}} \over {2.15}} = 480 \ne 160\)
=> điều giả sử ban đầu là sai
=> Cuộn dây không thuần cảm có điện trở r
- Ta có:
+ Ban đầu khi mắc vào hai đầu A, M một ắc quy có suất điện động E = 12V, điện trở trong r1 = 4W thì I1 = 0,1875
Theo định luật Ôm, ta có:
\({I_1} = {E \over {{R_b} + r}} = {E \over {{R_1} + r + {r_1}}} \to {R_1} + {r_1} + r = {E \over {{I_1}}} = 64 \to {R_1} + r = 60\Omega {\rm{ (1) }}\)
+ Khi mắc vào A,B một hiệu điện thế \(u = 120\sqrt 2 {\rm{cos100}}\pi {\rm{t}}\), R = R2 thì công suất tiêu thụ trên biến trở cực đại và bằng 160W
Ta có:
Công suất trên biến trở R đạt cực đại khi \({R_2}^2 = {r^2} + {\left( {{Z_L} - {Z_C}} \right)^2}{\rm{ (2)}}\)
Mặt khác, ta có:
Công suất trên R2:
\(\eqalign{
& P{\rm{ = }}{{{U^2}} \over {{{({R_2} + r)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R_2} = 160{\rm{W}} \to {{{R_2}} \over {{{({R_2} + r)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}} = {{160} \over {{{120}^2}}} = {1 \over {90}} \cr
& 90{R_2} = 2R_2^2 + 2{\rm{r}}R \to {R_2} + r = 45 \cr} \)
Kết hợp với (2) ta được: \(R_2^2 = {(45 - {R_2})^2} + {15^2} \to {R_2} = 25\Omega ,r = 20\Omega \)
Với r = 20W thay vào (1) => R1 = 60 - 20 = 40W
\( \to {{{R_1}} \over {{R_2}}} = {{40} \over {25}} = 1,6\)
Chọn A
Câu hỏi 8 :
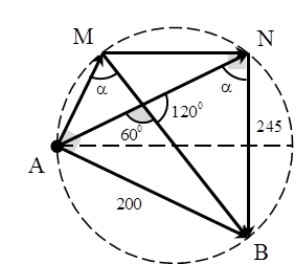
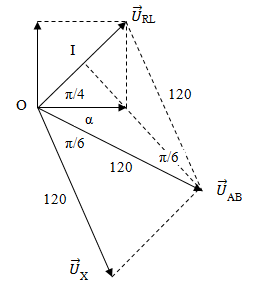
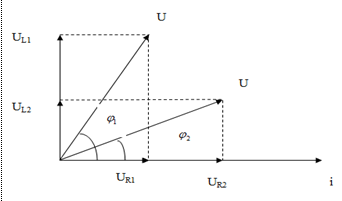
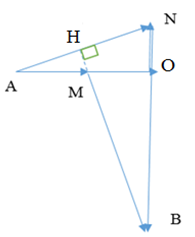
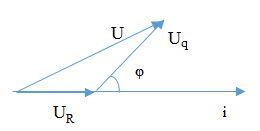
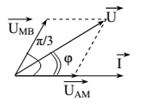
Cho mạch điện như hình vẽ, cuộn dây không thuần cảm, Hiệu điện thế hai đầu đoạn mạch là uAB=\(200\sqrt2\)cos100pt(V). Điện áp uAM vuông pha với uAB, uAN nhanh pha hơn uMB một góc \({{2\pi } \over 3}\) và UNB=245V. Hệ số công suất của đoạn mạch AB gần giá trị nào nhất?
- A 0,7
- B 0,5
- C 0,8
- D 0,6
Đáp án: A
Phương pháp giải:
áp dụng phương pháp giản đồ vectơ trong dòng điện xoay chiều
Lời giải chi tiết:
Đáp án A
Biễu diễn vecto các điện áp.
+ Ta thấy rằng MAB = MNB = 900→ M và N cùng nằm trên một đường tròn nhận
MB là đường kính.
AMB = ANB = α0 do cùng chắn cung AB.
+ Áp dụng định lý sin trong ΔANB, ta có:
với\({{200} \over {\sin \alpha }} = {{245} \over {\sin NAB}}\) NAB = 1800 – (600 + ABM)
Xét ΔAMB, ta có ABM = 900 – α => NAB = 300 +α
\(\eqalign{
& {{200} \over {\sin \alpha }} = {{245} \over {\sin \left( {{{30}^0} + \alpha } \right)}} = > \alpha = {54^0} = > NAB = {30^0} + {54^0} = {84^0} \cr
& = > ABN = {180^0} - {54^0} - {84^0} = {42^0} = > \varphi = {90^0} - ABN = {90^0} - {42^0} = {48^0} = > \cos \varphi = 0,67 \cr} \)
Câu hỏi 9 :
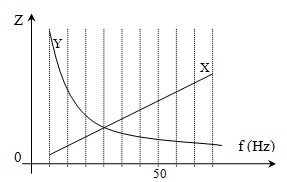
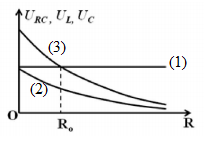
mạch điện gồm điện trở thuần R nối tiếp với hộp đen X và hộp đen Y. Biết X, Y là hai hộp có trở kháng phụ thuộc vào tần số như hình vẽ. Hiệu điện thế hiệu dụng hai đầu đoạn mạch là không đổi và bằng 210V. Khi thay đổi tần số dòng điện thì công suất tiêu thụ điện năng lớn nhất của mạch điện là 200W và khi đó điện áp trên X là 60V. Khi đưa tần số mạch điện tới giá trị là 50Hz thì công suất của mạch gần giá trị nào nhất?
- A 164,3 W
- B 173,3 W
- C 143,6 W
- D 179,4 W
Đáp án: D
Lời giải chi tiết:
Đáp án D
+ Ta thấy rằng đồ thi X có dạng là một đường thẳng xiên góc → X chứa cuộn dây ZX = L2πf.
Đồ thị Y có dạng là một hypebol → Y chứa tụ điện \({Z_Y} = {1 \over {C2\pi f}}\)
+ ZX = ZY → mạch xảy ra cộng hưởng, khi đó \(f = {f_0} = {4 \over 7}50Hz\)
+ Công suất tiêu thụ cực đại trên mạch →\({P_{max}} = {{{U^2}} \over R} = > 200 = {{{{210}^2}} \over R} \to {\rm{ }}R{\rm{ }} = {\rm{ }}220,5{\rm{ }}\Omega \) Cường độ dòng điện trong mạch \(I = {U \over R} = {{210} \over {220,5}} = {{20} \over {21}}A\)→ Cảm kháng và dung kháng tương ứng
+ Khi \(f = {7 \over 5}{f_0} = 50Hz\) thì dung kháng và cảm kháng tương ứng là
\(\left\{ \matrix{
Z{'_X} = {7 \over 4}{Z_X} = 110,25\Omega \hfill \cr
Z{'_Y} = {4 \over 7}{Z_Y} = 36\Omega \hfill \cr} \right.\)
→ Công suất tiêu thụ của mạch
\(P = {{{U^2}R} \over {{R^2} + \left( {Z{'_Y} - Z{'_X}} \right)}} = {{{{210}^2}.220,5} \over {220,{5^2} + {{(36 - 110,25)}^2}}} \approx 180W\)
Câu hỏi 10 :
Một đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM chỉ có biến trở R, đoạn mạch MB gồm tụ C mắc nối tiếp với cuộn dây không thuần cảm có độ tự cảm L, điện trở thuần r. Đặt vào AB một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi. Điều chỉnh R đến giá trị 80 Ω thì công suất tiêu thụ trên biến trở đạt cực đại, đồng thời tổng trở của đoạn mạch AB là số nguyên và chia hết cho 40. Khi đó hệ số công suất của đoạn mạch MB có giá trị là
- A 0,8.
- B 0,25.
- C 0,75.
- D 0,125.
Đáp án: D
Lời giải chi tiết:
Đáp án D
Phương pháp:Mạch điện xoay chiều có R thay đổi
Cách giải:
Điều chỉnh R đến giá trị 80Ω thì công suất tiêu thụ trên biến trở cực đại \( \Rightarrow R = \sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = 80\) (1)
Khi đó tổng trở của đoạn mạch là số nguyên và chia hết cho 40 => ZAB = 40n (n là số nguyên)\( \Rightarrow {Z_{AB}} = \sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = 40n \Leftrightarrow {\left( {80 + r} \right)^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = {\left( {40n} \right)^2}\) (2)
Từ (1) và (2) ta có:
\(\left\{ \matrix{
{r^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = {80^2} \hfill \cr
{\left( {80 + r} \right)^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = {\left( {40n} \right)^2} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{r^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = {80^2} \hfill \cr
{80^2} + 160r + {r^2} + {\left( {{Z_L} - {Z_C}} \right)^2} = {\left( {40n} \right)^2} \hfill \cr} \right. \Rightarrow r = 10{n^2} - 80\)
Hệ số công suất của đoạn MB là: \(c{\text{os}}{\varphi _{MB}} = \frac{r}{{\sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{{10{n^2} - 80}}{{80}}\)
Có: \(c{\text{os}}{\varphi _{MB}} \leqslant 1 \Leftrightarrow \frac{{10{n^2} - 80}}{{80}} \leqslant 1 \Rightarrow n \leqslant 4\)
+ Với n = 4 => cosφMB = 1
+ Với n = 3 \( \Rightarrow c{\text{os}}{\varphi _{MB}} = \frac{{{{10.3}^2} - 80}}{{80}} = 0,125\)
=> Chọn D
Câu hỏi 11 :
Lần lượt mắc một điện trở R, một cuộn dây, một tụ điện C vào cùng một nguồn điện ổn định và đo cường đọ dòng điện qua chúng thì được các giá trị ( theo thứ tự ) là 1A, 1A, và 0A; điện năng tiêu thụ trên R trong thời gian ∆t khi đó là Q. Sau đó mắc nối tiếp các linh kiện trên cùng với một ampe kế nhiệt lí tưởng vào một nguồn ổn định thứ hai thì số chỉ ampe kế là 1A. Biết nếu xét trong cùng thời gian ∆t thì: điện năng tiêu thụ trên R khi chỉ mắc nó vào nguồn thứ hai là 4Q; còn khi mắc cuộn dây vào nguồn này thì điện năng tiêu thụ trong thời gian này cũng là Q. Hỏi nếu mắc điện trở R nối tiếp với tụ và ampe kế nhiệt vào nguồn thứ hai thì ampe kế chỉ bao nhiêu?
- A 1A
- B 2A
- C
\[\sqrt 2 \]A - D 0,5A
Đáp án: A
Phương pháp giải:
sử dụng công thức tính điện năng tiêu thụ
Lời giải chi tiết:
Ban đầu cường độ dòng điện qua R. cuộn dây và C lần lượt là 1,1,0A, chứng tỏ dòng điện ban đầu là dòng điện không đổi, và cuộn dây có điện trở thuần bằng R
Sau đó dùng dòng điện xoay chiều.
Điên năng tiêu thụ ban đầu là :
\(Q = \frac{{{U^2}}}{R}.\Delta t\)
Điện năng tiêu thụ khi đặt vào dòng điện lúc sau và chỉ có R là:
\(\begin{gathered}
Q' = \frac{{U{'^2}}}{R}.\Delta t = 4Q = 4.\frac{{{U^2}}}{R} \hfill \\
= > U' = 2U \hfill \\
\end{gathered} \)
Khi cho dòng điện qua cuộn dây ta có:
\(\begin{gathered}
Q'' = \frac{{U{'^2}}}{{{{(R)}^2} + Z_L^2}}.R.\Delta t = Q = \frac{{{U^2}}}{R} \hfill \\
= > {Z_L} = \sqrt 3 .R \hfill \\
\end{gathered} \)
Khi mắc cả ba linh kiện vào dòng điện thừ 2 thì cường độ dòng điện là 1A. ta có:
\(\begin{gathered}
\frac{{U'}}{{\sqrt {{{\left( {2R} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \frac{U}{R} \hfill \\
= > {Z_C} = {Z_L} = \sqrt 3 R \hfill \\
\end{gathered} \)
Khi mắc điện trở với tụ vào mạch thứ hai thì cường độ dòng điện là:
\(I = \frac{{U'}}{{\sqrt {{R^2} + Z_C^2} }} = \frac{{2U}}{{2R}} = 1A\)
Câu hỏi 12 :
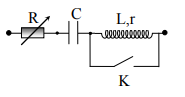
Đặt một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu một đoạn mạch như hình vẽ. Khi K đóng, điều chỉnh giá trị biến trở đến giá trị R1 hoặc R2 thì công suất tỏa nhiệt trên mạch đều bằng P. Độ lệch pha giữa điện áp tức thời hai đầu mạch và dòng điện trong mạch khi R = R1 là j1, khi R = R2 là j2, trong đó
\(\left| {{\varphi _1} - {\varphi _2}} \right| = \frac{\pi }{6}\)
. Khi K mở, điều chỉnh giá trị R từ 0 đến rất lớn thì công suất tỏa nhiệt trên biến trở R cực đại bằng 2P/3, công suất trên cả mạch cực đại bằng
\(\frac{{2P}}{{\sqrt 3 }}\)
. Hệ số công suất của cuộn dây là
- A
\(\frac{{\sqrt 3 }}{2}\) - B
\(\frac{1}{2}\) - C
\(\frac{{2\sqrt 3 }}{{\sqrt {13} }}\) - D
\(\frac{1}{{\sqrt {13} }}\)
Đáp án: D
Phương pháp giải:
Sử dụng biến dổi toán học và các điều kiện P cực trị
Lời giải chi tiết:
Khi K đóng, mạch chỉ có R, C mắc nối tiếp.
Khi R1, R2 thì P1 = P2nên:
\(\begin{array}{l}
\frac{{{U^2}.{R_1}}}{{{Z_1}}} = \frac{{{U^2}.{R_2}}}{{{Z_2}}} \Rightarrow \left\{ \begin{array}{l}
R{}_1 + {R_2} = \frac{{{U^2}}}{P}\\
{R_1}{R_2} = Z_C^2
\end{array} \right. * \\
\tan \Delta \varphi = \frac{{\tan {\varphi _1} - \tan {\varphi _2}}}{{1 - \tan {\varphi _1}.\tan {\varphi _2}}} = \tan \frac{\pi }{6} = \frac{1}{{\sqrt 3 }} \Leftrightarrow \frac{{ - \frac{{{Z_C}}}{{{R_1}}} - \frac{{ - {Z_C}}}{{{R_2}}}}}{{1 - \frac{{{Z_C}}}{{{R_1}}}.\frac{{{Z_C}}}{{{R_2}}}}} = \frac{1}{{\sqrt 3 }} \Rightarrow {R_1} + {R_2} = \frac{{2{Z_C}}}{{\sqrt 3 }}\\
* \Rightarrow {R_1} = {R_2} = \frac{{{Z_C}}}{{\sqrt 3 }} \Rightarrow P = \frac{{\sqrt {3.} {U^2}}}{{4{Z_C}}}
\end{array}\)
Khi K mở thì mạch R, r, L, C nối tiếp
Công suất mạch cực đại là:
\({P_{ma}} = \frac{{{U^2}}}{{2\left| {{Z_L} - {Z_C}} \right|}} = \frac{{{U^2}}}{{2({R_0} + r)}} = \frac{2}{{\sqrt 3 }}P \Rightarrow {Z_L} = 2{Z_C}\)
Công suất trên R cực đại:
\({P_{R\max }} = \frac{{{U^2}}}{{2R}} = \frac{{2P}}{3} \Leftrightarrow {R^2} = {r^2} + {({Z_L} - {Z_C})^2} \Rightarrow r = \frac{{{Z_C}}}{{\sqrt 3 }}\)
Thay các giá trị tìm được vào tính hệ số công suất cuộn dây:
\(\cos {\varphi _d} = \frac{r}{{\sqrt {{r^2} + {Z_L}^2} }} = \frac{1}{{\sqrt {13} }}\)
Đáp án D
Câu hỏi 13 :
Cho đoạn mạch AB gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L thay đổi được và tụ điện có điện dung C theo thứ tự đó mắc nối tiếp. Gọi M là điểm nối giữa R và cuộn cảm; N là điểm nối giữa cuộn cảm và tụ điện. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi. Cho L thay đổi, điện áp hiệu dụng hai đầu đoạn mạch AN và MN thay đổi theo đồ thị như hình vẽ. Khi L = L1 +L2 thì hệ số công suất của mạch là
- A cosφ = 0,86.
- B cosφ = 0,36.
- C cosφ = 0,96.
- D cosφ = 0,53.
Đáp án: B
Phương pháp giải:
Áp dụng công thức tính hệ số công suất của đoạn mạch xoay chiều mắc nối tiếp \(\cos \varphi = \frac{R}{Z}\)
Lời giải chi tiết:
Đáp án B
\({U_{RL}} > {U_L}\)=> Đường biểu diễn URL = UAN và đường dưới biểu diễn cho UL = UMN
\(\eqalign{
& {Z_L} = 0 = > {U_{RL}} = R{U \over {\sqrt {{R^2} + Z_C^2} }} = 140(1) \cr
& {Z_{{L_2}}} = > U_L^{max} = {{U\sqrt {{R^2} + Z_C^2} } \over R} = {{2000} \over 7}\buildrel {(1)} \over
\longrightarrow U = 200V\mathrel{\mathop{\kern0pt\longrightarrow}
\limits_{chon\,R = 1}^{(1)}} {Z_C} = {{\sqrt {51} } \over 7} \cr
& \left\{ \matrix{
{Z_{L1}} = {{{Z_C} + \sqrt {4{R^2} + Z_C^2} } \over R} = 1,63 \hfill \cr
{Z_{L2}} = {{{R^2} + Z_C^2} \over {{Z_C}}} = 2 \to {Z_{L1}} + {Z_{L2}} = 3,63 \hfill \cr} \right. = > \cos \varphi = {R \over {\sqrt {{R^2} + ({Z_{L12}} - {Z_C})} }} \approx 0,36 \cr} \)
Câu hỏi 14 :
Đặt điện áp xoay chiều có điện áp hiệu dụng U không đổi, tần số góc ω thay đổi được vào hai đầu đoạn mạch gồm cuộn cảm thuần có độ tự cảm L, điện trở thuần R và tụ điện có điện dung C mắc nối tiếp. Biết CR2 < 2L . Khi \(\omega = {\omega _1} = 100\pi \left( {rad/s} \right)\) hoặc \(\omega = {\omega _2} = 120\pi \left( {rad/s} \right)\)thì công suất tiêu thụ trong mạch như nhau. Khi ω = ω3 hoặc ω = ω3 + 40π (rad/s) thì điện áp hiệu dụng giữa hai bản tụ điện đều bằng 1,4U. Để điện áp hiệu dụng giữa hai bản tụ điện đạt giá trị cực đại thì ω phải có giá trị gần nhất với giá trị nào sau đây?
- A 112π rad/s.
- B 96π rad/s.
- C 84π rad/s.
- D 104π rad/s .
Đáp án: B
Phương pháp giải:
Áp dụng điều kiện ω biến thiên để trong mạch xuất hiện hiện tượng cộng hưởng điện \({\omega _0} = \sqrt {{\omega _1}{\omega _2}} \)
Định lý Vi-ét về tổng và tích của nghiệm trong phương trình bậc 2
Lời giải chi tiết:
Đáp án B
\(\begin{array}{l}{\omega _0} = \sqrt {{\omega _1}{\omega _2}} = \sqrt {100\pi .120\pi } = 20\pi \sqrt {30} \,rad/s\\{U_C} = \frac{U}{{\sqrt {{{\left( {\frac{\omega }{{{\omega _0}}}} \right)}^4} - 2{n^{ - 1}}{{\left( {\frac{\omega }{{{\omega _0}}}} \right)}^2} + 1} }} = > {\left( {\frac{\omega }{{{\omega _0}}}} \right)^4} - 2{n^{ - 1}}{\left( {\frac{\omega }{{{\omega _0}}}} \right)^2} + 1 - {\left( {\frac{U}{{{U_C}}}} \right)^2} = 0\end{array}\)
Theo định lý Vi – ét
\(\left\{ \matrix{
{\left( {{{{\omega _3}} \over {{\omega _0}}}} \right)^2} + {\left( {{{{\omega _3} + 40\pi } \over {{\omega _0}}}} \right)^2} = 2{n^{ - 1}} \hfill \cr
{\left( {{{{\omega _3}} \over {{\omega _0}}}} \right)^2}.{\left( {{{{\omega _3} + 40\pi } \over {{\omega _0}}}} \right)^2} = {{24} \over {49}} \hfill \cr} \right.\buildrel {{\omega _0} = 20\pi \sqrt {30} } \over
\longrightarrow \left\{ \matrix{
{\omega _0} = 232 \hfill \cr
n = 1,3 \hfill \cr} \right. = > {\omega _C} = {{{\omega _0}} \over {\sqrt n }} \approx 96\pi \)
Câu hỏi 15 :
Một đoạn mạch AB nối tiếp theo thứ tự gồm cuộn cảm thuần có độ tự cảm \(L = \frac{1}{{2\pi }}\left( H \right)\), điện trở R = 50Ω và hộp X. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(u = 120\sqrt 2 \cos 100\pi t\left( V \right)\)thì điện áp hiệu dụng của hộp X là 120V, đồng thời điện áp của hộp X trễ pha so với điện áp của đoạn mạch AB là π/6. Công suất tiêu thụ của hộp X có giá trị gần đúng là
- A 63W
- B 52W
- C 45W
- D 72W
Đáp án: B
Phương pháp giải:
Giản đồ vecto
Lời giải chi tiết:
Đáp án B
Ta có: \(R = 50\Omega ;{Z_L} = 100\pi .\frac{1}{{2\pi }} = 50\Omega ;{U_X} = 120V;U = 120V\)
Ta có giản đồ vecto
Ta có: \({U_{RL}} = 2.OI = 2.120.\sin 15 = 62V \Rightarrow I = \frac{{{U_{RL}}}}{{{Z_{RL}}}} = \frac{{62}}{{50\sqrt 2 }} = 0,878A\)
\(\begin{array}{l}\beta = \alpha + \frac{\pi }{4};\cos \beta = \frac{{OI}}{{{U_{AB}}}} = \frac{{31}}{{120}} \Rightarrow \beta = {75^0} \Rightarrow \alpha = {30^0}\\{\varphi _{{\rm{uX}}}} = \frac{\pi }{6} + \alpha = {60^0} \Rightarrow {P_X} = {U_X}I.\cos {\varphi _{{\rm{uX}}}} = 120.0,878.\cos 60 \approx 53W\end{array}\)
Câu hỏi 16 :
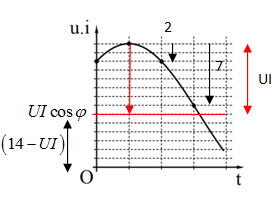
Đặt điện áp xoay chiều u vào hai đầu đoạn mạch có R, L, C mắc nối tiếp thì dòng điện trong đoạn mạch có cường độ i. Hình bên là một phần đồ thị biểu diễn sự phụ thuộc của tích u.i theo thời gian t. Hệ số công suất của đoạn mạch là
- A 0,625.
- B 0,866.
- C 0,500.
- D 0,707.
Đáp án: A
Lời giải chi tiết:
Đáp án A
\(\left\{ \begin{array}{l}u = {U_0}\cos (\omega t + {\varphi _u})\\i = {I_0}\cos (\omega t + {\varphi _i})\end{array} \right.;{\varphi _u} + {\varphi _i} = x;{\varphi _u} - {\varphi _i} = \varphi \)
\(p = ui = UI(\cos (2\omega t + x) + \cos \varphi )\)
13 =UI(1 + cosφ) (1) và 2ωt0 +x = 2π + k2π
t = 0, p = 11 = UI(cosx +cosφ) (2)
t = 3t0, p = 6 = UI(cos(2ω.3t0 +x) + cosφ)= UI(cos(6π-2x) + cosφ) = UI(cos(-2x) + cosφ) (3)
Lấy (1) chia (2) ta được cosφ = 5,5-6,5cosx
Lấy (1) chia (3) ta được \(\frac{{13}}{6}\)= ( 1 + cosφ)/(-cos(2x) + cosφ)= (1+5,5-6,5cosx)/(2.cos2x -1 +5,5 -6,5cosx)
Suy ra cosx = 0,75 => cosφ= 0,625
Câu hỏi 17 :
Đặt điện áp xoay chiều u vào hai đầu đoạn mạch có R, L, C mắc nối
tiếp thì dòng điện trong đoạn mạch có cường độ i. Hình bên là một phần đồ
thị biểu diễn sự phụ thuộc của tích u.i theo thời gian t. Hệ số công suất của
đoạn mạch là
- A 0,75.
- B 0,68.
- C 0,71.
- D 0,53.
Đáp án: A
Lời giải chi tiết:
Đáp án A
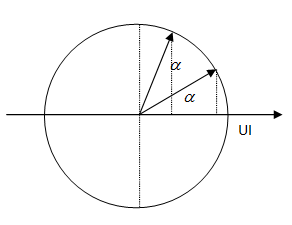
\(p = ui = {U_o}{I_o}c{\rm{os}}\omega {\rm{t}}{\rm{.cos}}\left( {\omega {\rm{t + }}\varphi } \right) = UI.c{\rm{os}}\left( {{\rm{2}}\omega {\rm{t + }}\varphi } \right) + UIc{\rm{os}}\varphi \), p biến thiên điều hòa quanh \({p_o} = UIc{\rm{os}}\varphi \) với biên độ U.I; Dùng vòng tròn lượng giác ta có
\(\left\{ \begin{array}{l}c{\rm{os}}\alpha {\rm{ = }}\frac{{{\rm{UI - 2}}}}{{{\rm{UI}}}}\\c{\rm{os2}}\alpha {\rm{ = }}\frac{{{\rm{UI - 7}}}}{{{\rm{UI}}}}\\c{\rm{os2}}\alpha {\rm{ = 2co}}{{\rm{s}}^{\rm{2}}}\alpha - 1\end{array} \right. \to UI = 8\); \(UIc{\rm{os}}\varphi {\rm{ = }}\left( {{\rm{14 - 8}}} \right) \to c{\rm{os}}\varphi {\rm{ = 0,75}}\)
Câu hỏi 18 :
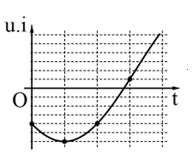
Đặt điện áp xoay chiều u vào hai đầu đoạn mạch có R, L, C mắc nối tiếp thì dòng điện trong đoạn mạch có cường độ i. Hình bên là một phần đồ thị biểu diễn sự phụ thuộc của tích u.i theo thời gian t. Hệ số công suất của đoạn mạch là
- A 0,71.
- B 0,50.
- C 0,25.
- D 0,20.
Đáp án: C
Lời giải chi tiết:
Đáp án C
\(p = ui = {U_o}{I_o}c{\rm{os}}\omega {\rm{t}}{\rm{.cos}}\left( {\omega {\rm{t + }}\varphi } \right) = UI.c{\rm{os}}\left( {{\rm{2}}\omega {\rm{t + }}\varphi } \right) + UIc{\rm{os}}\varphi \), p biến thiên điều hòa quanh \({p_o} = UIc{\rm{os}}\varphi \) với biên độ U.I; Dùng vòng tròn lượng giác ta có
\(\left\{ \begin{array}{l}c{\rm{os}}\alpha {\rm{ = }}\frac{{{\rm{UI - 2}}}}{{{\rm{UI}}}}\\c{\rm{os2}}\alpha {\rm{ = }}\frac{{{\rm{UI - 7}}}}{{{\rm{UI}}}}\\c{\rm{os2}}\alpha {\rm{ = 2co}}{{\rm{s}}^{\rm{2}}}\alpha - 1\end{array} \right. \to UI = 8\); \(UIc{\rm{os}}\varphi {\rm{ = }}\left( {{\rm{8 - 6}}} \right) \to c{\rm{os}}\varphi {\rm{ = 0,25}}\)
Câu hỏi 19 :
Cho mạch điện xoay chiều gồm ba phần tử R,L,C mắc nối tiếp, cuộn dây thuần cảm kháng. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều u = U0 cos (2πft) V, có f thay đổi được. Khi f = f1 thì công suất của mạch đạt giá trị cực đại. Khi f = f2 và f = f3thì cường độ hiệu dụng có giá trị không đổi. Biết
\(\frac{2}{{{f_2}}} + \frac{1}{{{f_3}}} = \frac{1}{{25}}\)
. Khi điều chỉnh
\(f = {f_4} \le 10\sqrt {10} Hz\)
thì URC không đổi. Khi đó f1 gần nhất với giá trị nào sau đây?
- A 90 Hz
- B 70 Hz
- C 80 Hz
- D 65 Hz
Đáp án: B
Phương pháp giải:
Áp dụng các điều kiện cộng hưởng, áp dụng BĐT cosi
Lời giải chi tiết:
Ta có khi f = f1 thì công suất cực đại ứng với hiện tượng cộng hưởng
\({\omega _1} = \frac{1}{{\sqrt {LC} }}\)
Khi f = f2 và f3 thì có cùng độ lớn cường độ dòng điện nên f2.f3 = f12
Mặt khác từ hệ thức đề bài ra, ta áp dụng BĐT Cosi :
\(\begin{array}{l}
\frac{2}{{{f_2}}} + \frac{1}{{{f_3}}} \ge 2.\sqrt {\frac{2}{{{f_2}{f_3}}}} \Leftrightarrow \frac{1}{{25}} \ge \frac{{2\sqrt 2 }}{{\sqrt {{f_2}{f_3}} }}\\
\Leftrightarrow {f_2}{f_3} \ge {25^2}.8 = 5000
\end{array}\)
Từ đó suy ra: \(LC \le \frac{1}{{20000{\pi ^2}}}\)
Mà khi f = f4 thì URC không đổi
\({U_{RC}} = I.{Z_{RC}} = \frac{{U.\sqrt {{R^2} + Z_C^2} }}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \frac{U}{{\sqrt {1 + \frac{{Z_L^2 - 2{Z_L}{Z_C}}}{{{R^2} + Z_C^2}}} }} = hs\)
Khi URC không đổi thì ZL = 2ZCsuy ra \(LC = \frac{2}{{\omega _4^2}}\)
Vậy \(LC = \frac{1}{{20000{\pi ^2}}}\)
Nên f1 = 70Hz
Câu hỏi 20 :
Một mạch điện xoay chiều gồm AM nối tiếp MB. Biết AM gồm điện trở thuần R1 , tụ điện C1, cuộn dây thuần cảm L1 mắc nối tiếp. Đoạn MB có hộp X, biết trong hộp X cũng có các phần tử là điện trở thuần, cuộn cảm, tụ điện mắc nối tiếp nhau. Đặt điện áp xoay chiều vào hai đầu mạch AB có tần số 50 Hz và giá trị hiệu dụng là 200V thì thấy dòng điện trong mạch có giá trị hiệu dụng 2A. Biết R1= 20Ω và nếu ở thời điểm t (s),\({u_{AB}} = 200\sqrt 2 V\) thì ở thời điểm \(\left( {t + \frac{1}{{600}}} \right)s\) dòng điện iAB = 0 (A) và đang giảm. Công suất của đoạn mạch MB là
- A 120W
- B 266,4W
- C 320W.
- D 400 W
Đáp án: A
Phương pháp giải:
Sử dụng công thức tính P, viết phương trình u, i
Lời giải chi tiết:
Tại t = 0 thì u = Uo => φu = 0
Tại t’ = t + 1/600 = t + T/12 thì i = 0 và đang giảm thì φi = π/2.
Nên suy ra tại thời điểm t pha của dòng điện là φi = π/3.
Vậy ta có phương trình của u và i như sau:
\(\begin{array}{l}
u = 200\sqrt 2 .\cos 100\pi t(V)\\
i = 2\sqrt 2 .\cos \left( {100\pi t + \frac{\pi }{3}} \right)(A)
\end{array}\)
Công suất tiêu thụ của đoạn mạch như sau:
P = I2.(R1 + R2) = I2.R1 + I2.R2 => PMB = I2.R2 = U.I – I2.R1 = 200.2-22.20 = 120W
Câu hỏi 21 :
Một đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM gồm điện trở thuần R1 mắc nối tiếp với tụ điện có điện dung C, đoạn mạch MB gồm điện trở thuần R2 mắc nối tiếp với cuộn cảm thuần có độ tự cảm L. Đặt điện áp xoay chiều có tần số và giá trị hiệu dụng không đổi vào hai đầu đoạn mạch AB. Khi đó đoạn mạch AB tiêu thụ công suất bằng 120 W và có hệ số công suất bằng 1. Nếu nối tắt hai đầu tụ điện thì điện áp hai đầu đoạn mạch AM và MB có cùng giá trị hiệu dụng nhưng lệch pha nhau π/3, công suất tiêu thụ trên đoạn mạch AB trong trường hợp này bằng
- A 75 W.
- B 90 W.
- C 160 W.
- D 180 W.
Đáp án: B
Phương pháp giải:
Phương pháp:
Vận dụng công thức tính hệ số công suất: ${\text{cos}}\varphi = \frac{R}{Z}$
Áp dụng điều kiện xảy ra hiện tượng cộng hưởng điện P = $\frac{{{U^2}}}{{{R_1} + {R_2}}}$
Lời giải chi tiết:
Đáp án B
Cách giải:
Ban đầu, mạch xảy ra cộng hưởng nên P = $\frac{{{U^2}}}{{{R_1} + {R_2}}}$= 120 Þ U2 = 120(R1+R2)
Lúc sau, khi nối tắt C, mạch còn R1R2L: Khi đó UAM = UMB ; Dj = π/3
Vẽ giản đồ ta có φ = $\frac{\pi }{6}$ à tanj = $\frac{{{Z_L}}}{{{R_1} + {R_2}}} = \frac{1}{{\sqrt 3 }} \Rightarrow {Z_L} = \frac{{{R_1} + {R_2}}}{{\sqrt 3 }}$
Khi đó P’ = I2(R1+ R2) = $\frac{{{U^2}({R_1} + {R_2})}}{{{{({R_1} + {R_2})}^2} + Z_L^2}}$=$\frac{{120{{({R_1} + {R_2})}^2}}}{{{{({R_1} + {R_2})}^2} + \frac{{{{({R_1} + {R_2})}^2}}}{3}}}$= 90 W
Câu hỏi 22 :
Đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn AM gồm điện trở thuần R1 = 40 W mắc nối tiếp với tụ điện có điện dung C = $\frac{{{{10}^{ - 4}}}}{{4\pi }}$F , đoạn mạch MB gồm điện trở thuần R2 mắc với cuộn thuần cảm. Đặt vào A, B điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi thì điện áp tức thời ở hai đầu đoạn mạch AM và MB lần lượt là uAM = 50$\root \of 2 $cos(100πt -$\frac{\pi }{4}$ )V; uMB = 150cos100πt V . Hệ số công suất của đoạn mạch AB là
- A 0,84.
- B 0,71.
- C 0,86.
- D 0,95.
Đáp án: A
Phương pháp giải:
Phương pháp:
Vận dụng công thức tính hệ số công suất: ${\text{cos}}\varphi = \frac{R}{Z}$
Lời giải chi tiết:
Đáp án A
Cách giải:
Xét đoạn mạch AM:
$\left\{ \matrix{
R = {Z_C} \Rightarrow {\phi _{AM}} = - {\pi \over 4} \hfill \cr
{Z_{AM}} = 40\sqrt 2 \Rightarrow I = {{{U_{AM}}} \over {{Z_{AM}}}} = 0,625\sqrt 2 A \hfill \cr} \right.$
Theo đề bài, uMB nhanh pha hơn uAM góc $\frac{\pi }{4}$ nên nhanh pha hơn i góc $\frac{\pi }{3}$
=> tanj = $\frac{{{Z_L}}}{{{R_2}}} = \sqrt 3 $ Þ ZL = $\root \of 3 $R2
Xét đoạn mạch MB: ZMB = $\frac{{{U_{MB}}}}{I} = 120 = \sqrt {R_2^2 + Z_L^2} = 2{R_2}$à R2 = 60 W; ZL = 60$\root \of 3 $ W
Hệ số công suất của mạch AB là cosφ = $\frac{{{R_1} + {R_2}}}{{\sqrt {{{({R_1} + {R_2})}^2} + {{({Z_L} + {Z_C})}^2}} }}$ » 0,84
Câu hỏi 23 :
Đặt một điện áp u = U\(\sqrt{2}\) cosωt (V) (U và ω không đổi) vào hai đầu đoạn mạch như hình vẽ. Biết ZL = \(\sqrt{3}\)R. Điều chỉnh C = C1 thì điện áp hiệu dụng giữa hai đầu tụ điện đạt cực đại thì hệ số công suất trong mạch là cosφ1. Điều chỉnh C = C2 để tổng điện áp hiệu dụng UAM + UMB đạt giá trị cực đại thì hệ số công suất trong mạch là cosφ2. Khi C = C3 thì hệ số công suất trong mạch là cosφ3 = cosφ1.cosφ2 và cường độ dòng điện trong mạch chậm pha hơn điện áp hai đầu đoạn mạch, khi đó tỉ số giữa điện trở thuần và dung kháng của tụ gần nhất với giá trị nào sau đây?
- A 0,42
- B 0,92
- C 2,37
- D 1,08
Đáp án: C
Phương pháp giải:
Tổng trở \(Z=\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}\)
Hệ số công suất cosφ = R/Z
Lời giải chi tiết:
UAM + UMB max
UMB = UC1cos(φ1 – φ2)
\(\tan \alpha =\frac{{{Z}_{L}}}{R}=\sqrt{3}\Rightarrow \alpha =\frac{\pi }{3}\)
\(\frac{U}{\sin \frac{\pi }{6}}=\frac{{{U}_{AM}}}{\sin (\frac{\pi }{2}-{{\varphi }_{2}})}=\frac{{{U}_{MB}}}{\sin ({{\varphi }_{2}}+\frac{\pi }{3})}\Rightarrow \frac{U}{\sin \frac{\pi }{6}}=\frac{{{U}_{AM}}+{{U}_{MB}}}{\sin (\frac{\pi }{2}-{{\varphi }_{2}})+\sin ({{\varphi }_{2}}+\frac{\pi }{3})}=\frac{{{U}_{AM}}+{{U}_{MB}}}{2\sin \frac{\pi }{12}.\sin (2{{\varphi }_{2}}-\frac{\pi }{6})}\)
\(\Rightarrow {{U}_{AM}}+{{U}_{MB}}=\frac{2U\sin \frac{5\pi }{12}}{\sin \frac{\pi }{6}}.\sin (2{{\varphi }_{2}}-\frac{\pi }{6})\Rightarrow {{\varphi }_{2}}=\frac{\pi }{3}\)
u\(\bot \) uRL nên φ1 = π/6
\(\text{cos}{{\varphi }_{3}}=c\text{os}{{\varphi }_{1}}.c\text{os}{{\varphi }_{2}}=\frac{\sqrt{3}}{4}\Rightarrow {{Z}_{C}}=\sqrt{13}-3\)
Khi đó: \(R\sqrt{3}={{Z}_{L}}\Rightarrow R=\sqrt{3}\)
Tỉ số R/ZC = 2,86
Chọn C
Câu hỏi 24 :
Trên đoạn mạch không phân nhành có bốn điểm theo đúng thứ tự A, M, N, B. Giữa A và M chỉ có điện trở thuần . Giữa M và N có một hộp kín X. Giữa N và B chỉ có cuộn cảm thuần có độ tự cảm L thay đổi được. Đặt vào hai đầu đoạn mạch AB một điện áp xoay chiều có biểu thức
\(u = {U_0}.\cos \left( {\omega t + \varphi } \right)\)
. Khi thay đổi L, người ta đo được công suất tiêu thụ của cả đoạn mạch luôn lớn gấp ba lần công suất tiêu thụ của đoạn mạch MB. Biết rằng khi L = 0, độ lệch pha giữa điện áp u và dòng điện trong mạch nhỏ hơn 200. Trong quá trình điều chỉnh L, góc lệch pha giữa điện áp tức thời của đoạn mạch MB so với điện áp tức thời của đoạn mạch Ab đạt giá trị lớn nhất bằng.
- A \(\frac{\pi }{4}\)
- B \(\frac{\pi }{3}\)
- C \(\frac{\pi }{2}\)
- D \(\frac{\pi }{6}\)
Đáp án: D
Phương pháp giải:
Sử dụng giản đồ vecto, kết hợp với công thức tan của một hiệu và bất đẳng thức côsi
Lời giải chi tiết:
Công suất tiêu thụ của đoạn mạch AB bằng 3 lần của đoạn MB nên ta có:
\(\begin{array}{l}
{P_{AB}} = 3{P_{MB}} \Leftrightarrow {I^2}.(R + {R_X}) = 3.{I^2}.{R_X}\\
\Rightarrow R = 2{R_X}
\end{array}\)
Khi L = 0 thì độ lệch pha giữa điện áp u và dòng điện trong mạch nhỏ hơn 200, vậy trong hộp kín X chỉ có RX
Ta có giản đồ:
Từ hình vẽ ta thấy góc lệch giữa uMB và uAB là α. Mà α = γ-β
Áp dụng công thức tan của một hiệu ta có:
\(\tan \alpha = \tan (\gamma - \beta ) = \frac{{\tan \gamma - \tan \beta }}{{1 + \tan \gamma .tan\beta }} = \frac{{\frac{L}{{{R_X}}} - \frac{L}{{3{R_X}}}}}{{1 + \frac{L}{{{R_X}}}.\frac{L}{{3{R_X}}}}} = \frac{2}{3}.\frac{{\frac{L}{{{R_X}}}}}{{1 + \frac{{{L^2}}}{{3R_X^2}}}}\)
Đặt \(\frac{L}{{{R_x}}} = x\) ta được
\(\tan \alpha = \frac{2}{3}.\frac{x}{{1 + \frac{{{x^2}}}{3}}}\)
Vì hàm tan là hàm đồng biến nên ta thấy khi α cực đại thì tan α cũng cực đại.
Áp dụng cosi cho biểu thức chứa x ta được:
\(\frac{x}{{1 + \frac{{{x^2}}}{3}}} = \frac{1}{{\frac{1}{x} + \frac{x}{3}}} \le \frac{1}{{2\sqrt {\frac{1}{3}} }}\)
Suy ra:
\(\begin{array}{l}
\tan \alpha \le \frac{2}{3}.\frac{1}{{2.\frac{1}{{\sqrt 3 }}}} = \frac{1}{{\sqrt 3 }}\\
\Rightarrow \alpha \le \frac{\pi }{6}
\end{array}\)
Vậy giá trị cực đại là
\(\frac{\pi }{6}\)
Chọn D
Câu hỏi 25 :
Đoạn mạch xoay chiều AB gồm điện trở R nối tiếp cuộn dây cảm thuần có độ tự cảm L thay đổi được, điện áp hai đầu cuộn cảm được đo bằng một vôn kế có điện trở rất lớn. khi L = L1 thì vôn kế chỉ U1, độ lệch pha giữa hai điện áp hai đầu đoạn mạch với dòng điện là φ1. Khi L = L2 thì vôn kế chỉ U2, độ lệch pha giữa điện áp hai đầu đoạn mạch và dòng điện là φ2. Biết \({\varphi _1} + {\varphi _2} = \frac{\pi }{2}ra{\rm{d}}\)
và \({U_1} = {U_2}\sqrt 2 \) . Hệ số công suất của mạch khi L = L1 có giá trị gần nhất với giá trị nào?
- A 0,82
- B 0,61
- C 0,75
- D 0,53
Đáp án: B
Phương pháp giải:
Sử dụng giản đồ vecto:
Và khi hai góc phụ nhau thì
Lời giải chi tiết:
Sử dụng giản đồ vecto:
Từ giản đồ vecto ta thấy:
\(\left\{ \begin{array}{l}
{U_{L1}} = U.\sin {\varphi _1}\\
{U_{R1}} = U.\cos {\varphi _1}\\
{U_{L2}} = U.\sin {\varphi _2}\\
{U_{R2}} = U.\cos {\varphi _2}
\end{array} \right. \Rightarrow {U_{L1}} = \sqrt 2 {U_{L2}} \Leftrightarrow U.\sin {\varphi _1} = \sqrt 2 U.\sin {\varphi _2}\)
Vì:
\(\begin{array}{l}
{\varphi _1} + {\varphi _2} = \frac{\pi }{2} \Rightarrow \sin {\varphi _2} = \cos {\varphi _1} \Rightarrow U.\sin {\varphi _1} = \sqrt 2 U.\cos {\varphi _1}\\
\Rightarrow \tan {\varphi _1} = \sqrt 2 \Rightarrow \cos {\varphi _1} = \cos (\arctan \sqrt 2 ) = 0,577
\end{array}\)
Chọn B
Câu hỏi 26 :
Cho mạch điện như hình vẽ, hai cuộn dây thuần cảm có độ tự cảm thay đổi, biết R2 = 5R1. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(u = U\sqrt 2 cos\omega t\) (Với U và ω không đổi). Điều chỉnh độ tự cảm của các cuộn dây (nhưng luôn thỏa mãn L2 = 0,8L1) sao cho độ lệch pha giữa điện áp hai đầu đoạn mạch AM và MB lớn nhất, thì hệ số công suất của đoạn mạch khi đó bằng
![]()
- A 0,8
- B 0,6
- C \(\frac{8}{{\sqrt {73} }}\)
- D \(\frac{6}{{\sqrt {73} }}\)
Đáp án: A
Phương pháp giải:
- Chuẩn hoá số liệu
- Công thức tính độ lệch pha giữa u và i : \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
- Hệ số công suất : \(\cos \varphi = \frac{R}{Z}\)
- Công thức lượng giác : \(\tan \left( {{\varphi _1} - {\varphi _2}} \right) = \frac{{\tan {\varphi _1} - \tan {\varphi _2}}}{{1 + \tan {\varphi _1}.\tan {\varphi _2}}}\)
- Bất đẳng thức Cô – si : \(a + b \ge 2\sqrt {ab} \)
Dấu ‘’=’’ xảy ra khi a = b
Lời giải chi tiết:
Ta có: \({L_2} = 0,8{L_1} \Rightarrow {Z_{L2}} = 0,8{Z_{L1}}\)
Đặt: \(\left\{ \begin{array}{l}{Z_{L1}} = x\\{Z_{L2}} = 0,8x\\{R_1} = 1\\{R_2} = 5\end{array} \right.\)
Ta có:
\(\begin{array}{l}\tan \Delta \varphi = \tan \left( {{\varphi _{AM}} - {\varphi _{MB}}} \right) = \frac{{\tan {\varphi _{AM}} - \tan {\varphi _{MB}}}}{{1 + \tan {\varphi _{AM}}.\tan {\varphi _{MB}}}} = \frac{{\frac{{{Z_{L1}}}}{{{R_1}}} - \frac{{{Z_{L2}}}}{{{R_2}}}}}{{1 + \frac{{{Z_{L1}}}}{{{R_1}}}.\frac{{{Z_{L2}}}}{{{R_2}}}}}\\\tan \Delta \varphi = \frac{{\frac{x}{1} - \frac{{0,8x}}{5}}}{{1 + \frac{x}{1} - \frac{{0,8x}}{5}}} = \frac{{0,84x}}{{1 + 0,16{x^2}}} = \frac{{0,84}}{{\frac{1}{x} + 0,16x}}\\ \Rightarrow {\left( {\tan \Delta \varphi } \right)_{\max }} \Leftrightarrow {\left( {\frac{1}{x} + 0,16x} \right)_{\min }}\end{array}\)
Áp dụng bất đẳng thức Cô – si ta có : \({\left( {\frac{1}{x} + 0,16x} \right)_{\min }} \Leftrightarrow \frac{1}{x} = 0,16x \Rightarrow x = 2,5\)
→ Hệ số công suất của đoạn mạch khi đó :
\(\cos \varphi = \frac{{{R_1} + {R_2}}}{{\sqrt {{{\left( {{R_1} + {R_2}} \right)}^2} + {{\left( {{Z_1} + {Z_2}} \right)}^2}} }} = \frac{{1 + 5}}{{\sqrt {{{\left( {1 + 5} \right)}^2} + {{\left( {2,5 + 0,8.2,5} \right)}^2}} }} = 0,8\)
Chọn A
Câu hỏi 27 :
Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu đoạn mạch AB mắc nối tiếp gồm biến trở R và cuộn cuộn cảm thuần L. Gọi φ là độ lệch pha của điện áp hai đầu đoạn mạch và cường độ dòng điện trong đoạn mạch. Hình vẽ là đồ thị của công suất mà mạch tiêu thụ theo giá trị của φ. Giá trị của φ1 gần giá trị nào nhất sau đây ?
- A 0,48rad
- B 0,52rad
- C 0,42rad
- D 0,32rad
Đáp án: C
Phương pháp giải:
Phương pháp :
Áp dụng công thức tính công suất\(P = UI\cos \varphi \)
Phương pháp chuẩn hóa số liệu
Lời giải chi tiết:
Cách giải :
Công suất của mạch đạt giá trị cực đại khi \(P = UI\cos \varphi = \frac{{{U^2}R}}{{{R^2} + Z_L^2}} = \frac{{{U^2}}}{{R + \frac{{Z_L^2}}{R}}}\)
Để công suất đạt cực đại khi
Hệ số công suất của mạch khi đó là \(\cos \varphi = \frac{1}{{\sqrt 2 }}\) .
Công suất của mạch có giá trị cực đại là \({P_{max}} = \frac{{{U^2}}}{{2{Z_L}}}\)
Từ đồ thị ta thấy tại thời điểm \({\varphi _1}\) công suất của mạch bằng \(\frac{3}{4}\)công suất cực đại ta có
\(P = U{I_1}\cos {\varphi _1} = \frac{{{U^2}.R}}{{R_1^2 + Z_L^2}} = \frac{3}{4}\frac{{{U^2}}}{{2{Z_L}}} = > 8{Z_L}.{R_1} = 3R_1^2 + 3Z_L^2 = > 3R_1^2 - 8{Z_L}.{R_1} + 3Z_L^2 = 0\)
Chuẩn hóa \({Z_L} = 1\) khi đó ta có phương trình \(3R_1^2 - 8{R_1} + 3 = 0 = > \left( \begin{array}{l}{R_1} = \frac{{4 + \sqrt 7 }}{3}\\{R_1} = \frac{{4 - \sqrt 7 }}{3}\end{array} \right.\)
Với \({R_1} = \frac{{4 + \sqrt 7 }}{3} = > \cos {\varphi _1} = \frac{{{R_1}}}{Z} = \frac{{\frac{{4 + \sqrt 7 }}{3}}}{{\sqrt {{{\left( {\frac{{4 + \sqrt 7 }}{3}} \right)}^2} + {1^2}} }} = > {\varphi _1} = 0,42rad\)
Với \({R_1} = \frac{{4 - \sqrt 7 }}{3} = > \cos {\varphi _1} = \frac{{{R_1}}}{Z} = \frac{{\frac{{4 - \sqrt 7 }}{3}}}{{\sqrt {{{\left( {\frac{{4 - \sqrt 7 }}{3}} \right)}^2} + {1^2}} }} = > {\varphi _1} = 1,18rad\)
Chọn C
Câu hỏi 28 :
Cho một đoạn mạch điện gồm một biến trở R mắc nối tiếp với một tụ điện có \(C = {{100} \over \pi }(\mu F)\) . Đặt vào hai đầu đoạn mạch một điện áp xoay chiều ổn định u với tần số góc 100π (rad/s). Thay đổi R ta thấy với hai giá trị của R là R = R1 và R = R2 thì công suất của đoạn mạch đều bằng nhau. Tích R1R2 có giá trị bằng
- A 10
- B 100
- C 1000
- D 10000
Đáp án: D
Phương pháp giải:
Áp dụng công thức tính công suất tiêu thụ:
\(P = U.I.\cos \varphi = \frac{{{U^2}}}{{{R^2} + Z_C^2}}.R\)
Lời giải chi tiết:
Ta có:
\({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi .\frac{{100}}{\pi }{{.10}^{ - 6}}}} = 100\Omega \)
Công thức tính công suất tiêu thụ:
\(P = U.I.\cos \varphi = \frac{{{U^2}}}{{{R^2} + Z_C^2}}.R\)
Mà P1 = P2 nên ta có :
\(\begin{array}{l}
\frac{{{U^2}}}{{{R_1}^2 + Z_C^2}}.{R_1} = \frac{{{U^2}}}{{{R_2}^2 + Z_C^2}}.{R_2} \Rightarrow R{}_1.({R_2}^2 + Z_C^2) = {R_2}.({R_1}^2 + Z_C^2)\\
\Leftrightarrow {R_1}.{R_2}.({R_1} - {R_2}) = {Z_C}^2.({R_1} - {R_2}) \Rightarrow {R_1}.{R_2} = {Z_C}^2 = 10000
\end{array}\)
Chọn D
Câu hỏi 29 :
Đặt điện áp xoay chiều có tần số không đổi vào hai đầu đoạn mạch AB gồm điện trở thuần R, tụ điện C và cuộn cảm thuần L (L thay đổi được). Khi L = L0 thì điện áp hiệu dụng giữa hai đầu cuộn cảm đạt cực đại và bằng \({{\text{U}}_{\text{Lmax}}}\). Khi L = L1 hoặc L = L2 thì điện áp hiệu dụng giữa hai đầu cuộn cảm có giá trị như nhau và bằng UL. Biết rằng UL/ULmax = k. Tổng hệ số công suất của mạch AB khi L = L1 và L = L2 là n.k. Hệ số công suất của mạch AB khi L = L0 có giá trị bằng ?
- A \(\frac{\text{n}}{\sqrt{2}}\)
- B \(\text{n}\sqrt{\text{2}}\)
- C \(\frac{\text{n}}{\text{2}}\)
- D \(\text{n}\)
Đáp án: C
Phương pháp giải:
Dùng phương pháp đại số: Xác định công thức tính \(\text{cos }{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{0}}}\),\(\text{cos }{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{1}}}\)và \(\text{cos }{{\text{ }\!\!\varphi\!\!\text{ }}_{2}}\)từ mối quan hệ giữa UL và ULmax. Sau đó sử dụng dữ kiện còn lại tính \(\text{cos }{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{0}}}\).
Lời giải chi tiết:
Khi L = L0 thì ULmax nên ta có:
\({{\text{Z}}_{\text{L0}}}\text{ = }\frac{{{\text{R}}^{\text{2}}}\text{ + Z}_{\text{C}}^{\text{2}}}{{{\text{Z}}_{\text{C}}}}\) và \(\text{cos }{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{0}}}\text{ = }\frac{\text{R}}{{{\text{Z}}_{\text{0}}}}\text{ = }\frac{\text{R}}{\sqrt{{{\text{R}}^{\text{2}}}\text{ + }\frac{{{\text{R}}^{\text{4}}}}{\text{Z}_{\text{C}}^{\text{2}}}}}=\frac{{{\text{Z}}_{\text{C}}}}{\sqrt{\text{Z}_{\text{C}}^{\text{2}}\text{ + }{{\text{R}}^{\text{2}}}}}=\frac{\sqrt{\text{Z}_{\text{C}}^{\text{2}}\text{ + }{{\text{R}}^{\text{2}}}}}{{{\text{Z}}_{\text{L0}}}}\)
Khi L = L1 hoặc L = L2 thì điện áp hiệu dụng giữa hai đầu cuộn cảm có giá trị như nhau và bằng UL:
\(\frac{\text{U}{{\text{Z}}_{\text{L1}}}}{{{\text{Z}}_{\text{1}}}}\text{ = }\frac{\text{U}{{\text{Z}}_{\text{L2}}}}{{{\text{Z}}_{\text{2}}}}\Leftrightarrow \frac{{{\text{Z}}_{\text{L1}}}}{\sqrt{{{\text{R}}^{\text{2}}}\text{+}{{\left( {{\text{Z}}_{\text{L1}}}-{{\text{Z}}_{\text{C}}} \right)}^{\text{2}}}}}\text{=}\frac{{{\text{Z}}_{\text{L2}}}}{\sqrt{{{\text{R}}^{\text{2}}}\text{+}{{\left( {{\text{Z}}_{\text{L2}}}-{{\text{Z}}_{\text{C}}} \right)}^{\text{2}}}}}\Leftrightarrow \frac{{{\text{R}}^{\text{2}}}\text{+}{{\left( {{\text{Z}}_{\text{L1}}}-{{\text{Z}}_{\text{C}}} \right)}^{\text{2}}}}{\text{Z}_{\text{L1}}^{\text{2}}}=\frac{{{\text{R}}^{\text{2}}}\text{+}{{\left( {{\text{Z}}_{\text{L2}}}-{{\text{Z}}_{\text{C}}} \right)}^{\text{2}}}}{\text{Z}_{\text{L2}}^{\text{2}}}\)
\(\Leftrightarrow \frac{{{\text{R}}^{\text{2}}}\text{ + Z}_{\text{C}}^{\text{2}}}{\text{Z}_{\text{L1}}^{\text{2}}}-\frac{\text{2}{{\text{Z}}_{\text{C}}}}{{{\text{Z}}_{\text{L1}}}}=\frac{{{\text{R}}^{\text{2}}}\text{ + Z}_{\text{C}}^{\text{2}}}{\text{Z}_{\text{L2}}^{\text{2}}}-\frac{\text{2}{{\text{Z}}_{\text{C}}}}{{{\text{Z}}_{\text{L2}}}}\Leftrightarrow \left( {{\text{R}}^{\text{2}}}\text{ + Z}_{\text{C}}^{\text{2}} \right)\left( \frac{1}{\text{Z}_{\text{L1}}^{\text{2}}}-\frac{1}{\text{Z}_{\text{L2}}^{\text{2}}} \right)=2{{\text{Z}}_{\text{C}}}\left( \frac{1}{{{\text{Z}}_{\text{L1}}}}-\frac{1}{{{\text{Z}}_{\text{L2}}}} \right)\)
\(\Leftrightarrow \frac{1}{{{\text{Z}}_{\text{L1}}}}+\frac{1}{{{\text{Z}}_{\text{L2}}}}=2\frac{{{\text{Z}}_{\text{C}}}}{{{\text{R}}^{\text{2}}}\text{ + Z}_{\text{C}}^{\text{2}}}\Leftrightarrow \frac{1}{{{\text{Z}}_{\text{L1}}}}+\frac{1}{{{\text{Z}}_{\text{L2}}}}=\frac{2}{{{\text{Z}}_{\text{L0}}}}\)
Theo đề bài ta có:
\(\frac{{{\text{U}}_{\text{L}}}}{{{\text{U}}_{\text{Lmax}}}}\text{ = }\frac{\text{U}\text{.}{{\text{Z}}_{\text{L1}}}}{\sqrt{{{\text{R}}^{\text{2}}}\text{+}{{\left( {{\text{Z}}_{\text{L1}}}-{{\text{Z}}_{\text{C}}} \right)}^{\text{2}}}}}.\frac{\text{R}}{\text{U}\sqrt{{{\text{R}}^{\text{2}}}\text{ + Z}_{\text{C}}^{\text{2}}}}=\frac{\text{R}}{{{\text{Z}}_{\text{1}}}}\text{.}\frac{{{\text{Z}}_{\text{L1}}}}{\sqrt{{{\text{R}}^{\text{2}}}\text{ + Z}_{\text{C}}^{\text{2}}}}=\text{cos }{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{1}}}.\frac{{{\text{Z}}_{\text{L1}}}}{\sqrt{{{\text{R}}^{\text{2}}}\text{ + Z}_{\text{C}}^{\text{2}}}}\)
\(\Rightarrow \text{cos }{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{1}}}\text{.}\frac{{{\text{Z}}_{\text{L1}}}}{\sqrt{{{\text{R}}^{\text{2}}}\text{ + Z}_{\text{C}}^{\text{2}}}}\text{ = k}\Rightarrow \text{cos }{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{1}}}=\frac{\text{k}\sqrt{{{\text{R}}^{\text{2}}}\text{ + Z}_{\text{C}}^{\text{2}}}}{{{\text{Z}}_{\text{L1}}}}\)
Tương tự ta có: \(\text{cos }{{\text{ }\!\!\varphi\!\!\text{ }}_{2}}=\frac{\text{k}\sqrt{{{\text{R}}^{\text{2}}}\text{ + Z}_{\text{C}}^{\text{2}}}}{{{\text{Z}}_{\text{L2}}}}\)
Mặt khác: \(\text{cos}{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{1}}}\text{ + cos}{{\text{ }\!\!\varphi\!\!\text{ }}_{2}}\text{ = nk}\Leftrightarrow \frac{\text{k}\sqrt{{{\text{R}}^{\text{2}}}\text{ + Z}_{\text{C}}^{\text{2}}}}{{{\text{Z}}_{\text{L1}}}}+\frac{\text{k}\sqrt{{{\text{R}}^{\text{2}}}\text{ + Z}_{\text{C}}^{\text{2}}}}{{{\text{Z}}_{\text{L2}}}}=\text{nk}\Leftrightarrow \sqrt{{{\text{R}}^{\text{2}}}\text{ + Z}_{\text{C}}^{\text{2}}}\left( \frac{1}{{{\text{Z}}_{\text{L1}}}}+\frac{1}{{{\text{Z}}_{\text{L2}}}} \right)=\text{n}\)
\(\Leftrightarrow \sqrt{{{\text{R}}^{\text{2}}}\text{ + Z}_{\text{C}}^{\text{2}}}.\frac{2}{{{\text{Z}}_{\text{L0}}}}=\text{n}\Leftrightarrow 2\text{cos }{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{0}}}=\text{n}\Leftrightarrow \text{cos }{{\text{ }\!\!\varphi\!\!\text{ }}_{\text{0}}}=\frac{\text{n}}{\text{2}}\)
Chọn C
Câu hỏi 30 :
Đoạn mạch nối tiếp gồm cuộn cảm thuần, đoạn mạch X và tụ điện (hình vẽ).
Khi đặt vào hai đầu A, B điện áp \({{u}_{AB}}\text{ }=\text{ }{{U}_{O}}cos\left( \omega t\text{ }+\text{ }\varphi \right)\) (V);
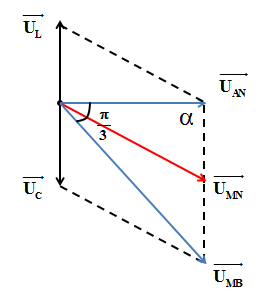
\(Uo,\omega \) và không đổi thì: \(LC{{\omega }^{2}}=1\), ${{U}_{AN}}=30\sqrt{2}V$ và ${{U}_{MB}}=60\sqrt{2}V$, đồng thời UMB trễ pha so với UAN . Nếu cảm kháng của cuộn dây là 15W thì công suất của đoạn mạch A, B có giá trị gần đúng nhất là
- A 79 W
- B 104 W
- C 60 W
- D 112W
Đáp án: B
Phương pháp giải:
Sử dụng giản đồ vecto
Sử dụng các định lí hàm số sin, hàm số cos:
\(\begin{array}{l}
{c^2} = {a^2} + {b^2} - 2ab.cos\varphi \\
\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}
\end{array}\)
Công suất của mạch: \(P=UI\cos \varphi \)
Lời giải chi tiết:
Áp dụng định lý hàm số cos:
\(\frac{{{U_L} + {U_C}}}{{\sin \frac{\pi }{3}}} = \frac{{{U_{MB}}}}{{\sin \alpha }} \Rightarrow \sin \alpha = \frac{{60\sqrt 2 .\sin \frac{\pi }{3}}}{{30\sqrt 6 }} = 1 \Rightarrow \alpha = {90^o}\)
Lại có \(LC{{\omega }^{2}}=1\)
\(\Rightarrow {{U}_{L}}={{U}_{C}}=15\sqrt{6}(V)\)
Dòng điện trong mạch: \(I=\frac{{{U}_{L}}}{{{Z}_{L}}}=\frac{15\sqrt{6}}{15}=\sqrt{6}\) (A)
Áp dụng định lý hàm số sin:\(\frac{{{U}_{L}}+{{U}_{C}}}{\sin \frac{\pi }{3}}=\frac{{{U}_{MB}}}{\sin \alpha }\Rightarrow \sin \alpha =\frac{60\sqrt{2}.\sin \frac{\pi }{3}}{30\sqrt{6}}=1\Rightarrow \alpha ={{90}^{o}}\) :
\(\Rightarrow {{U}_{MN}}=\sqrt{U_{AN}^{2}+U_{L}^{2}}=15\sqrt{14}\) (V)
Vì \({{U}_{L}}={{U}_{C}}\to {{U}_{AB}}={{U}_{MN}}\), \(\text{cos}\varphi \text{=}\frac{{{U}_{AN}}}{{{U}_{MN}}}=\frac{2\sqrt{7}}{7}\)
Công suất của mạch: \(P=UI\cos \varphi =60\sqrt{3}\approx 104\) (W)
Chọn B
Câu hỏi 31 :
Đặt điện áp xoay chiều có tần số 50 Hz và giá trị hiệu dụng không đổi vào hai đầu đoạn mạch có R, L, C mắc nối tiếp, độ tự cảm L thay đổi được. Điều chỉnh L đến các giá trị \(L={{L}_{1}}=\frac{\sqrt{3}}{\pi }\)H và \(L={{L}_{2}}=\frac{3\sqrt{3}}{\pi }\)H thì công suất tiêu thụ của đoạn mạch bằng nhau và độ lệch pha của điện áp so với cường độ dòng điện trong đoạn mạch tương ứng là \({{\varphi }_{1}}\)và \({{\varphi }_{2}}.\)Biết \(\left| {{\varphi }_{1}} \right|+\left| {{\varphi }_{2}} \right|={{120}^{0}}\). Điện trở R bằng
- A \(\frac{100}{\sqrt{3}}\text{ }\!\!\Omega\!\!\text{ }\)
- B \(\text{100 }\!\!\Omega\!\!\text{ }\)
- C \(\text{100}\sqrt{3}\text{ }\!\!\Omega\!\!\text{ }\)
- D \(\text{100}\sqrt{2}\text{ }\!\!\Omega\!\!\text{ }\)
Đáp án: B
Phương pháp giải:
Áp dụng: Khi L = L1 và L = L2 thì \({{P}_{1}}={{P}_{2}}\Leftrightarrow {{Z}_{1}}={{Z}_{2}}\Leftrightarrow \left| {{Z}_{L1}}-{{Z}_{C}} \right|=\left| {{Z}_{L2}}-{{Z}_{C}} \right|\Rightarrow -{{Z}_{L1}}+{{Z}_{C}}={{Z}_{L2}}-{{Z}_{C}}\)
\(\Rightarrow {{Z}_{C}}=\frac{{{Z}_{L2}}+{{Z}_{L1}}}{2}\)
Và: \(\tan {{\varphi }_{1}}=-\tan {{\varphi }_{2}}\Rightarrow \left| {{\varphi }_{1}} \right|=\left| {{\varphi }_{2}} \right|\)
Lời giải chi tiết:
Ta có: \(\omega =100\pi \Rightarrow {{Z}_{L1}}=100\sqrt{3}(\Omega );{{Z}_{L2}}=300\sqrt{3}(\Omega )\)
Khi L = L1 và L = L2 thì \({{P}_{1}}={{P}_{2}}\Leftrightarrow {{Z}_{1}}={{Z}_{2}}\Leftrightarrow \left| {{Z}_{L1}}-{{Z}_{C}} \right|=\left| {{Z}_{L2}}-{{Z}_{C}} \right|\Rightarrow -{{Z}_{L1}}+{{Z}_{C}}={{Z}_{L2}}-{{Z}_{C}}\)
\(\Rightarrow {{Z}_{C}}=\frac{{{Z}_{L2}}+{{Z}_{L1}}}{2}=200\sqrt{3}(\Omega )\)
Và: \(\tan {{\varphi }_{1}}=-\tan {{\varphi }_{2}}\Rightarrow \left| {{\varphi }_{1}} \right|=\left| {{\varphi }_{2}} \right|={{60}^{o}}\Rightarrow \tan {{\varphi }_{1}}=\frac{{{Z}_{L1}}-{{Z}_{C}}}{R}=-\sqrt{3}\)
\(\Rightarrow R=100(\Omega )\)
Chọn B
Câu hỏi 32 :
Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đôi vào hai đầu đoạn mạch AB mắc nối tiếp theo thứ tự gôm cuộn cảm thuân L, biên trở R và tụ điện C. Gọi URC là điện áp hiệu dụng ở hai đầu đoạn mạch gồm tụ C và biến trở R, UC là điện áp hiệu dụng ở hai đầu tụ C, UL là điện áp hiệu dụng hai đầu cuộn cảm thuần L. Hình bên là đồ thị biểu diễn sự phụ thuộc của URC, UL và UC theo giá trị của biến trở R. Khi R = 2R0, thì hệ số công suất của đoạn mạch AB xấp xỉ là
- A 0,96.
- B 0,79.
- C 0,63.
- D 0,85.
Đáp án: A
Phương pháp giải:
Phương pháp:
Sử dụng các công thức: \({{U}_{RC}}=\frac{U.\sqrt{{{R}^{2}}+Z_{C}^{2}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\), \({{U}_{C}}=\frac{U.{{Z}_{C}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\); \({{U}_{L}}=\frac{U.{{Z}_{L}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\)
Hệ số công suất của mạch: \(\cos \varphi =\frac{R}{Z}\)
Lời giải chi tiết:
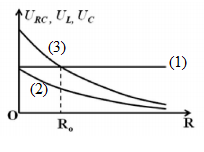
Ta có: \({{U}_{RC}}=\frac{U.\sqrt{{{R}^{2}}+Z_{C}^{2}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\), \({{U}_{C}}=\frac{U.{{Z}_{C}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\); \({{U}_{L}}=\frac{U.{{Z}_{L}}}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\)
+ Khi R thay đổi, UC và UL đều chắc chắn biến thiên. Vậy đường đồ thị (1) chỉ có thể là URC. Để URC không đổi, ZL-ZC =ZC => ZL=2.ZC
Khi R=O , \({{U}_{RC}}=\frac{U.{{Z}_{C}}}{{{Z}_{L}}-{{Z}_{C}}}={{U}_{C}}\). Vậy đường đồ thị (2) biểu diễn UC, còn đường đồ thị (3) biểu diễn UL
Khi R=RO\({{U}_{RC}}={{U}_{L}}\to \frac{U.\sqrt{{{R}_{O}}^{2}+Z_{C}^{2}}}{\sqrt{{{R}_{O}}^{2}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}=\frac{U.{{Z}_{L}}}{\sqrt{{{R}_{O}}^{2}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}\to {{R}_{O}}^{2}+Z_{C}^{2}=Z_{L}^{2}\to {{R}_{O}}=\sqrt{3}.{{Z}_{C}}\)
Khi R= 2RO =\(2\sqrt{3}.{{Z}_{C}}\), hệ số công suất của đoạn mạch AB \(\cos \varphi =\frac{R}{Z}=\frac{2\sqrt{3}.{{Z}_{C}}}{\sqrt{{{(2\sqrt{3}.{{Z}_{C}})}^{2}}+Z_{C}^{2}}}=0,96\)
Chọn A
Câu hỏi 33 :
Một đoạn mạch điện gồm đoạn mạch X mắc nối tiếp với đoạn mạch Y. Đoạn mạch Y gồm điện trở thuần 30 \(\Omega \) và cuộn cảm thuần có độ tự cảm \(\frac{0,4}{\pi }H\), sau đó đặt vào hai đầu đoạn mạch chứa X và Y một điện áp xoay chiều \(u={{U}_{o}}\text{cos}\omega \text{t}\) thì đồ thị điện áp tức thời của đoạn mạch X và đoạn mạch Y như hình bên. Nếu mắc cả đoạn mạch X và đoạn mạch Y với đoạn mạch T( Gồm điện trở thuần 80\(\Omega \) và tụ điện có điện dung\(\frac{{{10}^{-4}}}{\pi }F\)) nối tiếp, rồi mắc vào điện áp xoay chiều như trên thì công suất tiêu thụ của đoạn mạch là:
- A 125W
- B 50W
- C 37,5W
- D
75W
Đáp án: B
Phương pháp giải:
Sử dụng hàm phức
Lời giải chi tiết:
Từ đồ thị ta có: T=0,02s \(\to \omega =100\pi \);\({{u}_{Y}}=50\text{cos100}\pi \text{t}\text{, }{{u}_{X}}=75\text{cos100}\pi \text{t}\)
Điện áp của mạch: \(u={{u}_{X}}+{{u}_{Y}}=50\text{cos100}\pi \text{t+}75\text{cos100}\pi \text{t=12}5\text{cos100}\pi \text{t}\)(V)
Cảm kháng của cuộn dây trong Y là: \({{Z}_{L}}=40\Omega \)
Tổng trở đoạn mạch Y: \({{\bar{Z}}_{Y}}=30+40i\)
Dòng điện trong mạch: \(\bar{i}=\frac{{{u}_{Y}}}{{{{\bar{Z}}}_{Y}}}=0,6-0,8i(A)\)
Tổng trở đoạn mạch X: \({{\bar{Z}}_{X}}=\frac{{{u}_{X}}}{{\bar{i}}}=45+60i\)
Tổng trở đoạn mạch T: \({{\bar{Z}}_{T}}=80-100i\)
Tổng trở cả mạch : \(\bar{Z}={{\bar{Z}}_{Y}}+{{\bar{Z}}_{X}}+{{\bar{Z}}_{T}}=155(\Omega )\)
Công suất tiêu thụ của đoạn mạch :\(P=\frac{{{U}^{2}}}{Z}=50(W)\)
Chọn B
Câu hỏi 34 :
Một đoạn mạch gồm điện trở thuần R, cuộn dây cảm thuần có độ tự cảm L, tụ điện có điện dung C thay đổi được mắc nối tiếp. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(u = U\sqrt 2 .\cos \left( {100\pi t} \right)V\). Khi C = C1thì công suất tiêu thụ của mạch là P = 100W và cường độ dòng điện qua mạch có biểu thức \(i = {I_0}.\cos \left( {100\pi t + \frac{\pi }{3}} \right)A\). Khi C = C2, công suất tiêu thụ của mạch đạt cực đại. Giá trị cực đại đó là:
- A 100 W
- B 400 W
- C 200 W
- D 150 W.
Đáp án: B
Phương pháp giải:
Công suất tiêu thụ : \(P = {I^2}.R = \frac{{{U^2}.R}}{{{R^2} + {{({Z_L} - {Z_C})}^2}}}\)
Độ lệch pha giữa u và i được xác định :
\(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R}\)
Thay đổi C để P cực đại thì tức là xảy ra cộng hưởng, khi đó
\({P_{\max }} = \frac{{{U^2}}}{R}\)
Lời giải chi tiết:
Khi C = C1 thì độ lệch pha giữa u và i được xác định:
\(\begin{array}{l}
\tan \varphi = \frac{{{Z_L} - {Z_{{C_1}}}}}{R} \Rightarrow \tan \frac{{ - \pi }}{3} = \frac{{{Z_L} - {Z_C}_1}}{R} = - \sqrt 3 \\
\Rightarrow {Z_L} - {Z_{{C_1}}} = - \sqrt 3 .R
\end{array}\)
Áp dụng công thức tính công suất:
\(\begin{array}{l}
P = {I^2}.R = \frac{{{U^2}.R}}{{{R^2} + {{({Z_L} - {Z_{{C_1}}})}^2}}} \Rightarrow 100 = \frac{{{U^2}.R}}{{{R^2} + {{({Z_L} - {Z_{C1}})}^2}}}\\
\Rightarrow 100 = \frac{{{U^2}.R}}{{{R^2} + {{( - \sqrt 3 R)}^2}}} = \frac{{{U^2}}}{{4.R}}
\end{array}\)
Thay đổi C để P cực đại thì tức là xảy ra cộng hưởng, khi đó:
\({P_{\max }} = \frac{{{U^2}}}{R} = 4.\frac{{{U^2}}}{{4.R}} = 4.100 = 400{\rm{W}}\)
Chọn B.
Câu hỏi 35 :
Đặt điện áp \(u = U\sqrt 2 \cos \omega t\,\,\left( V \right)\) (với U, ω không đổi) vào hai đầu đoạn mạch mắc nối tiếp gồm \(R = 150\,\,\Omega \), tụ điện có điện dung C, cuộn cảm thuần có độ tự cảm L. Lúc này công suất tỏa nhiệt trên điện trở là P. Nếu tháo tụ điện ra khỏi mạch thì công suất tỏa nhiệt trên điện trở còn \(\dfrac{P}{3}\). Tổng cảm kháng nhỏ nhất và dung kháng nhỏ nhất thỏa mãn bài toán có giá trị xấp xỉ
- A \(385,3\,\,\Omega \)
- B \(288,6\,\,\Omega \)
- C \(282,8\,\,\Omega \)
- D \(259,6\,\,\Omega \)
Đáp án: A
Phương pháp giải:
Công suất tiêu thụ: \(P = \dfrac{{{U^2}R}}{{{Z^2}}} = \dfrac{{{U^2}R}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}\)
Phương trình bậc 2: \(a{x^2} + bx + c = 0\) có nghiệm khi \(\Delta = {b^2} - 4ac \ge 0\)
Lời giải chi tiết:
Khi chưa tháo tụ điện ra khỏi mạch, công suất nhiệt trên điện trở là:
\(P = \dfrac{{{U^2}R}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}} = \dfrac{{{U^2}.150}}{{{{150}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}\)
Khi tháo tụ điện ra khỏi mạch thì công suất toả nhiệt trên điện trở là:
\(P' = \dfrac{{{U^2}R}}{{{R^2} + Z_L^2}} = \dfrac{{{U^2}.150}}{{{{150}^2} + Z_L^2}}\)
Theo bài ra ta có:
\(\begin{array}{l}P' = \dfrac{P}{3} \Leftrightarrow \dfrac{{{U^2}.150}}{{{{150}^2} + Z_L^2}} = \dfrac{1}{3}.\dfrac{{{U^2}.150}}{{{{150}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}\\ \Leftrightarrow 3.\left[ {{{150}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \right] = {150^2} + Z_L^2\\ \Leftrightarrow 3.\left( {{{150}^2} + Z_L^2 - 2.{Z_L}.{Z_C} + Z_C^2} \right) = {150^2} + Z_L^2\\ \Leftrightarrow {3.150^2} + 3Z_L^2 - 6{Z_L}.{Z_C} + 3Z_C^2 = {150^2} + Z_L^2\\ \Leftrightarrow 2Z_L^2 - \left( {6.{Z_C}} \right).{Z_L} + 3Z_C^2 + 45000 = 0\,\,\left( 1 \right)\\ \Leftrightarrow 3Z_C^2 - \left( {6{Z_L}} \right).{Z_C} + 2Z_L^2 + 45000 = 0\,\,\,\left( 2 \right)\end{array}\)
Xét phương trình bậc 2 đối với ẩn ZL. Điều kiện để (1) có nghiệm là:
\(\begin{array}{l}\Delta = {\left( {6{Z_C}} \right)^2} - 4.2.\left( {3Z_C^2 + 45000} \right) \ge 0\\ \Leftrightarrow 36Z_C^2 - 24Z_C^2 - 360000 \ge 0\\ \Leftrightarrow {Z_C} \ge 173,2\Omega \Rightarrow {Z_{C\min }} = 173,2\Omega \,\,\,\,\,\left( * \right)\end{array}\)
Xét phương trình bậc 2 đối với ẩn ZC. Điều kiện để (2) có nghiệm là:
\(\begin{array}{l}\Delta = {\left( {6{Z_L}} \right)^2} - 4.3.\left( {2Z_C^2 + 45000} \right) \ge 0\\ \Leftrightarrow 36Z_L^2 - 24Z_C^2 - 540000 \ge 0\\ \Leftrightarrow {Z_L} \ge 212,1\Omega \Rightarrow {Z_{L\min }} = 212,1\Omega \,\,\,\,\left( {**} \right)\end{array}\)
Từ (*) và (**) ta có:
\({Z_{L\min }} + {Z_{C\min }} = 173,2 + 212,1 = 385,3\Omega \)
Chọn A.
Câu hỏi 36 :
Đặt điện áp \(u = {U_0}\cos \omega t\)(Uo và ω không đổi) vào hai đầu đoạn mạch AB theo thứ tự gồm một tụ điện, một cuộn cảm thuần và một điện trở thuần mắc nối tiếp. Gọi M là điểm nối giữa tụ điện và cuộn cảm. Biết điện áp hiệu dụng giữa hai đầu MB gấp \(\sqrt 3 \) lần điện áp hiệu dụng giữa hai đầu AM và cường độ dòng điện trong đoạn mạch lệch pha \(\dfrac{\pi }{6}\) so với điện áp giữa hai đầu đoạn mạch. Hệ số công suất của đoạn mạch MB là
- A \(0,5\sqrt 2 \)
- B 1
- C \(0,5\sqrt 3 \)
- D 0,5
Đáp án: D
Phương pháp giải:
Độ lệch pha giữa u và i: \(\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R}\)
Hệ số công suất của đoạn mạch MB: \(\cos {\varphi _{RL}} = \dfrac{R}{{\sqrt {{R^2} + Z_L^2} }}\)
Lời giải chi tiết:
Theo bài ra ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}{U_{MB}} = \sqrt 3 .{U_{AM}} \Leftrightarrow \sqrt {{R^2} + Z_L^2} = \sqrt 3 {Z_C}\\\tan \left( {\dfrac{\pi }{6}} \right) = \dfrac{{{Z_L} - {Z_C}}}{R} = \dfrac{1}{{\sqrt 3 }}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{R^2} + Z_L^2 = 3Z_C^2 \Leftrightarrow \dfrac{{Z_L^2}}{{{R^2}}} - 3\dfrac{{Z_C^2}}{{{R^2}}} + 1 = 0\\\dfrac{{{Z_L}}}{R} - \dfrac{{{Z_C}}}{R} = \dfrac{1}{{\sqrt 3 }}\end{array} \right.\\\end{array}\)
Đặt:
\(\begin{array}{l}\left\{ \begin{array}{l}\dfrac{{{Z_L}}}{R} = x\\\dfrac{{{Z_C}}}{R} = y\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x^2} - 3{y^2} + 1 = 0\\x - y = \dfrac{1}{{\sqrt 3 }} \Rightarrow y = x - \dfrac{1}{{\sqrt 3 }}\end{array} \right.\\ \Rightarrow {x^2} - 3.{\left( {x - \dfrac{1}{{\sqrt 3 }}} \right)^2} + 1 = 0\\ \Leftrightarrow {x^2} - 3\left( {{x^2} - \dfrac{2}{{\sqrt 3 }}x + \dfrac{1}{3}} \right) + 1 = 0\\ \Leftrightarrow {x^2} - 3{x^2} + 2\sqrt 3 x - 1 + 1 = 0\\ \Leftrightarrow - 2{x^2} + 2\sqrt 3 x = 0 \Leftrightarrow x = \sqrt 3 \Rightarrow \dfrac{{{Z_L}}}{R} = \sqrt 3 \end{array}\)
Hệ số công suất của đoạn mạch MB là:
\(\cos {\varphi _{MB}} = \dfrac{R}{{\sqrt {{R^2} + Z_L^2} }} = \dfrac{1}{{\sqrt {1 + {x^2}} }} = \dfrac{1}{{\sqrt {1 + {{\left( {\sqrt 3 } \right)}^2}} }} = 0,5\)
Chọn D.
Câu hỏi 37 :
Đặt điện áp \(u = U\sqrt 2 .\cos \omega t\,\,\left( V \right)\)(với U và ω không đổi) vào hai đầu đoạn mạch AB như hình vẽ. R là biến trở, cuộn cảm thuần có độ tự cảm L, tụ điện có điện dung C. Biết \(LC{\omega ^2} = 2\). Gọi P là công suất tiêu thụ của đoạn mạch AB. Đồ thị trong hệ tọa độ vuông góc ROP biểu diễn sự phụ thuộc của P vào R trong trường hợp K mở ứng với đường (1) và trong trưởng hợp K đóng ứng với đường (2) như hình vẽ. Giá trị của điện trở r bằng :
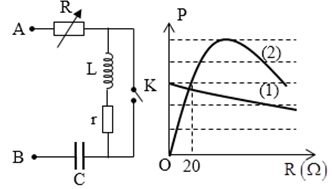
- A 20Ω
- B 60Ω
- C 180Ω
- D 90Ω
Đáp án: C
Phương pháp giải:
Công thức tính cảm kháng, dung kháng: \(\left\{ \begin{array}{l}{Z_L} = \omega L\\{Z_C} = \dfrac{1}{{\omega C}}\end{array} \right.\)
Công suất tiêu thụ của mạch khi K đóng: \({P_d} = \dfrac{{{U^2}R}}{{{R^2} + Z_C^2}}\)
Công suất tiêu thụ của đoạn mạch khi K mở: \({P_m} = \dfrac{{{U^2}.\left( {R + r} \right)}}{{{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}\)
Kết hợp các công thức và kĩ năng đọc đồ thị để khai thác được các dữ kiện từ đồ thị.
Lời giải chi tiết:
Ta có đồ thị như hình vẽ:
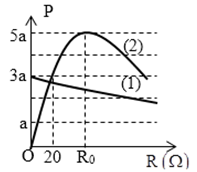
Từ dữ kiện: \(LC{\omega ^2} = 2 \Rightarrow \dfrac{{{Z_L}}}{{{Z_C}}} = 2 \Rightarrow {Z_L} = 2{Z_C}\)
+ Khi K đóng mạch gồm R nt C. Công suất tiêu thụ của đoạn mạch khi đó:
\({P_d} = \dfrac{{{U^2}R}}{{{R^2} + Z_C^2}} = \dfrac{{{U^2}}}{{R + \dfrac{{Z_C^2}}{R}}} \Rightarrow {P_{d\max }} = \dfrac{{{U^2}}}{{2R}} \Leftrightarrow R = {Z_C}\)
Từ đồ thị ta thấy: \({P_{d\max }} = \dfrac{{{U^2}}}{{2{R_0}}} = \dfrac{{{U^2}}}{{2{Z_C}}} = 5a\,\,\left( 1 \right)\)
Chú ý khi Pđ đạt cực đại thì \({R_0} = {Z_C} > 20\Omega \)
Tại giá trị R = 20Ω ta có : \({P_d} = \dfrac{{{U^2}.20}}{{{{20}^2} + Z_C^2}} = 3a\,\,\left( 2 \right)\)
Lấy (1) chia (2) ta có:
\(\begin{array}{l}\dfrac{{{{20}^2} + Z_C^2}}{{40.{Z_C}}} = \dfrac{5}{3} \Leftrightarrow 3Z_C^2 - 200{Z_C} + 1200 = 0\\ \Leftrightarrow \left[ \begin{array}{l}{Z_C} = 60\Omega \,\,\left( {t/m} \right)\\{Z_C} = \dfrac{{20}}{3} < 20\,\,\left( {loai} \right)\end{array} \right. \Rightarrow {Z_C} = 60\Omega \end{array}\)
+ Khi K mở mạch gồm: \(R - L,r - C\)
Công suất tiêu thụ của mạch:
\({P_m} = \dfrac{{{U^2}.\left( {R + r} \right)}}{{{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}} = \dfrac{{{U^2}.\left( {R + r} \right)}}{{{{\left( {R + r} \right)}^2} + Z_C^2}}\)
Từ đồ thị ta thấy:\(R = 0 \Rightarrow {P_m} = \dfrac{{{U^2}.r}}{{{r^2} + Z_C^2}} = 3a\,\,\,\left( 3 \right)\)
Từ (2) và (3) ta có:
\(\begin{array}{l}\dfrac{{{U^2}.20}}{{{{20}^2} + Z_C^2}} = \dfrac{{{U^2}.r}}{{{r^2} + Z_C^2}} \Leftrightarrow \dfrac{{20}}{{20 + {{60}^2}}} = \dfrac{r}{{{r^2} + {{60}^2}}}\\ \Leftrightarrow {r^2} - 200r + 3600 = 0 \Rightarrow r = 180\Omega \end{array}\)
(Chú ý rằng \(r > \left| {{Z_L} - {Z_C}} \right|\))
Chọn C.
Câu hỏi 38 :
Đặt điện áp xoay chiều u = U0. Cos 100πt (V) vào hai đầu đoạn mạch AB như hình vẽ. Hình bên là đồ thị biểu diễn điện áp uAN và uMB phụ thuộc vào thời gian t. Biết công suất tiêu thụ trên đoạn AM bằng công suất tiêu thụ trên đoạn MN. Hệ số công suất của mạch AB nhận giá trị gần giá trị nào sau đây nhất:
- A 0,83
- B 0,86
- C 0,74
- D 0,76
Đáp án: A
Phương pháp giải:
+ Từ đồ thị ta thấy điện áp cực đại của uANlà 30 V , pha ban đầu bằng 0, vì vậy ta có phương trình điện áp:
\({u_{AN}} = 30.cos\left( {\omega t} \right)\)
+ Từ đồ thị ta thấy điện áp cực đại của uMBlà \(30\sqrt 2 (V)\), pha ban đầu bằng \(\frac{{ - \pi }}{2}\) , vì vậy ta có phương trình điện áp:
\({u_{MB}} = 30\sqrt 2 .cos\left( {\omega t - \frac{\pi }{2}} \right)(cm)\)
+ Vì công suất tiêu thụ trên AM bằng công suất tiêu thụ trên MN nên ta có:
\(\;{I^2}.R{\rm{ }} = {I^2}.r \Leftrightarrow R = r\)
Vẽ giản đồ vecto. Sử dụng giản đồ vecto và các dữ kiện bài cho để giải.
Lời giải chi tiết:
Từ đồ thị ta thấy điện áp cực đại của uAN là 30 V , pha ban đầu bằng 0, vì vậy ta có phương trình điện áp:
\({u_{AN}} = 30.cos\left( {\omega t} \right)\)
+ Từ đồ thị ta thấy điện áp cực đại của uMBlà \(30\sqrt 2 (V)\), pha ban đầu bằng \(\frac{{ - \pi }}{2}\) , vì vậy ta có phương trình điện áp:
\({u_{MB}} = 30\sqrt 2 .cos\left( {\omega t - \frac{\pi }{2}} \right)(cm)\)
Vì công suất tiêu thụ trên AM bằng công suất tiêu thụ trên MN nên ta có:
\(\;{I^2}.R{\rm{ }} = {I^2}.r \Leftrightarrow R = r\)
Ta có giản đồ vecto như hình sau:
với \({U_{AN}} = 15\sqrt 2 V;{U_{MB}} = \;30V\)
Ta có :
\(\Delta AON \sim \Delta BOM \Rightarrow \frac{{AO}}{{BO}} = \frac{{AN}}{{BM}} = \frac{{15\sqrt 2 }}{{30}} = \frac{1}{{\sqrt 2 }} \Rightarrow BO = \frac{1}{{\sqrt 2 }}.AO\)
Trong tam giác OMB ta có:
\(M{B^2} = O{M^2} + O{B^2} = O{M^2} + {\left( {\frac{1}{{\sqrt 2 }}OA} \right)^2}\)
Mà OM = OA nên :
\(M{B^2} = \frac{3}{2}O{A^2} \Leftrightarrow OA = \frac{{\sqrt 3 }}{{\sqrt 2 }}MB = \frac{{\sqrt 3 }}{{\sqrt 2 }}.30 = 15\sqrt 6 V\)
Vì vậy ta có \(OB = \frac{1}{{\sqrt 2 }}.OA = \frac{1}{{\sqrt 2 }}.15\sqrt 6 = 15{\sqrt 3 _{}}(V)\)
Ta có:
\(AB = \sqrt {O{A^2} + O{B^2}} = \sqrt {{{(15\sqrt 6 )}^2} + {{\left( {15\sqrt 3 } \right)}^2}} = {45_{}}V\)
Hệ số công suất là
\(\cos \varphi = \frac{{AO}}{{AB}} = \frac{{15\sqrt 6 }}{{45}} = \frac{{\sqrt 2 }}{{\sqrt 3 }} = 0,82\)
Chọn A
Câu hỏi 39 :
Một quạt điện xoay chiều mắc nối tiếp với điện trở R rồi mắc hai đầu đoạn mạch này vào điện áp xoay chiều có giá trị hiệu dụng 380 V. Biết quạt điện này có giá trị định mức 220V – 80 W và khi hoạt động đúng công suất định mức thì độ lệch pha giữa điện áp ở hai đầu quạt và cường độ dòng điện chạy qua nó là φ với cosφ = 0,8. Để quạt điện chạy gần đúng công suất định mức nhất thì R có giá trị
- A 230,4Ω
- B 360,7Ω
- C 396,7Ω
- D 180,4Ω
Đáp án: C
Phương pháp giải:
Ta coi đoạn mạch gồm R nối tiếp quạt là điện trở R nối tiếp với đọan mạch RLC nối tiếp.
Áp dụng công thức tính công suất của quạt \(P = U.I.\cos \varphi \) ta tính được cường độ dòng điện I
Vẽ giản đồ vecto của đoạn mạch.
Từ đó ta tìm được UR từ giản đồ vecto:
\(U = \sqrt {U_R^2 + U_q^2 - 2{U_R}.{U_q}.\cos ({{180}^0} - \varphi )} \)
Xác định được điện trở R:
\(R = \frac{{{U_R}}}{I}\)
Lời giải chi tiết:
Áp dụng công thức tính công suất của quạt:
\(P = U.I.\cos \varphi \Rightarrow I = \frac{P}{{U.\cos \varphi }} = \frac{{80}}{{220.0,8}} = \frac{5}{{11}}A\)
Mạch điện có giản đồ vecto:
Từ đó ta tìm được UR từ giản đồ vecto:
\(\begin{gathered}
U = \sqrt {U_R^2 + U_q^2 - 2{U_R}.{U_q}.\cos ({{180}^0} - \varphi )} \hfill \\
\Leftrightarrow {380^2} = U_R^2 + {220^2} - 2.{U_R}.220.( - \cos \varphi ) \Rightarrow {U_R} = 180V \hfill \\
\end{gathered} \)
Xác định được điện trở R:
\(R = \frac{{{U_R}}}{I} = \frac{{180}}{{\frac{5}{{11}}}} = {396_{}}\Omega \)
Chọn C.
Câu hỏi 40 :
Đặt điện áp \(u = {U_0}{\cos ^2}\left( {\omega t + \varphi } \right)\) vào hai đầu đoạn mạch gồm biến trở R, cuộn cảm thuần L và tụ điện C mắc nối tiếp. Khi biến trở có giá trị R = 25Ω và R = 75Ω thì công suất tiêu thụ của đoạn mạch bằng nhau và bằng 100W. Giá trị của U0 là:
- A \(200\frac{{\sqrt 2 }}{{\sqrt 3 }}V\)
- B \(200\sqrt 2 V\)
- C 100V
- D \(100\sqrt 2 V\)
Đáp án: B
Phương pháp giải:
Biến đổi
\(u = {U_0}.{\cos ^2}\left( {\omega t + \varphi } \right) = {U_0}.\left( {\frac{{1 + \cos \left( {2\omega t + 2\varphi } \right)}}{2}} \right)\)
Khi có hai giá trị R1 và R2cùng cho một công suất P thì:
\(P = \frac{{{U^2}}}{{{R_1} + {R_2}}}\)
Chú ý: tụ điện chỉ cho dòng điện xoay chiều đi qua.
Lời giải chi tiết:
Biến đổi:
\(\begin{gathered}
u = {U_0}.{\cos ^2}\left( {\omega t + \varphi } \right) = {U_0}.\left( {\frac{{1 + \cos \left( {2\omega t + 2\varphi } \right)}}{2}} \right) \hfill \\
\,\,\,\, = \frac{{{U_0}}}{2} + \frac{{{U_0}}}{2}.\cos \left( {2\omega t + 2\varphi } \right) \hfill \\
\end{gathered} \)
Vậy dòng điện có hai thành phần, thành phần thứ nhất là dòng điện không đổi, thành phần thứ hai là dòng điện xoay chiều.
Vì mạch của ta có RLC nối tiếp, mà tụ điện chỉ cho dòng điện xoay chiều đi qua, nên mạch chỉ do thành phần xoay chiều đi qua mạch.
Khi có hai giá trị R1 và R2 cùng cho một công suất P thì: \(P = \frac{{{U^2}}}{{{R_1} + {R_2}}}\)
Vậy ta có :
\(P = \frac{{{U^2}}}{{{R_1} + {R_2}}} = \frac{{{{\left( {\frac{{{U_0}}}{{2\sqrt 2 }}} \right)}^2}}}{{(25 + 75)}} = 100 \Rightarrow {U_0} = 200{\sqrt 2 _{}}V\)
Chọn B.
Câu hỏi 41 :
Đặt điện áp xoay chiều có dạng \(u = U\sqrt 2 cos\left( {2\pi f} \right)V\) vào hai đầu đoạn mạch gồm R, L, C mắc nối tiếp với U không đổi, \(R = \sqrt {\dfrac{L}{C}} \) , f thay đổi được. Khi \(f = {f_1}\) và \(f = {f_2}\) thì công suất tiêu thụ của đoạn mạch như nhau bằng \({P_0}\). Khi \(f = {f_3}\) thì điện áp hiệu dụng ở hai đầu tụ điện đạt giá trị cực đại và công suất tiêu thụ của đoạn mạch lúc này là \(P\). Biết rằng \(\dfrac{{{f_1} + {f_2}}}{{{f_3}}} = \dfrac{9}{2}\). Tỉ số \(\dfrac{{{P_0}}}{P}\) bằng
- A \(\dfrac{{51}}{3}.\)
- B \(\dfrac{4}{{19}}.\)
- C \(\dfrac{{19}}{4}.\)
- D \(\dfrac{3}{{51}}.\)
Đáp án: C
Phương pháp giải:
+ Vận dụng bài toán f biến thiên
+ Sử dụng biểu thức tính công suất: \(P = \dfrac{{{U^2}R}}{{{Z^2}}}\)
Lời giải chi tiết:
Khi \(f = {f_1}\) và \(f = {f_2}\) thì mạch có cùng công suất \({P_0}\) , ta có:
\(\begin{array}{l}{P_1} = {P_2} = {P_0}\\ \Leftrightarrow cos{\varphi _1} = cos{\varphi _2}\\ \Leftrightarrow \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_{L1}} - {Z_{C1}}} \right)}^2}} }} = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_{L2}} - {Z_{C2}}} \right)}^2}} }}\\ \Leftrightarrow {Z_{L1}} + {Z_{L2}} = {Z_{{C_1}}} + {Z_{C2}}\\ \Leftrightarrow L\left( {{\omega _1} + {\omega _2}} \right) = \dfrac{1}{C}\left( {\dfrac{1}{{{\omega _1}}} + \dfrac{1}{{{\omega _2}}}} \right)\end{array}\)
\( \Rightarrow \dfrac{1}{{LC}} = {\omega _1}{\omega _2}\) (1)
Để \({U_{{C_{max}}}}\) khi đó \({\omega _3} = \dfrac{1}{{LC}} - \dfrac{{{R^2}}}{{2{L^2}}}\)
Theo đề bài ta có: \(R = \sqrt {\dfrac{L}{C}} \Rightarrow {R^2} = \dfrac{L}{C} \Rightarrow {R^2} = {Z_{L1}}{Z_{C1}}\)
\( \Rightarrow \omega _3^2 = \dfrac{1}{{LC}} - \dfrac{{\dfrac{L}{C}}}{{2{L^2}}} = \dfrac{1}{{2LC}}\) (2)
Lại có \(\dfrac{{{f_1} + {f_2}}}{{{f_3}}} = \dfrac{{{\omega _1} + {\omega _2}}}{{{\omega _3}}} = \dfrac{9}{2}\) (3)
Từ (1), (2) ta suy ra: \({\omega _1}{\omega _2} = 2\omega _3^2\)
Kết hợp vớ (3) ta suy ra: \(\left\{ \begin{array}{l}{\omega _1} = 8{\omega _2} = 4{\omega _3}\\{\omega _2} = \dfrac{{{\omega _3}}}{2}\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}{Z_{{L_1}}} = 8{Z_{L2}} = 4{Z_{L3}}\\{Z_{C1}} = \dfrac{{{Z_{C2}}}}{8} = \dfrac{{{Z_{C3}}}}{4}\end{array} \right.\)
Ta có
\(\begin{array}{l}{Z_{L1}} + {Z_{L2}} = {Z_{C1}} + {Z_{{C_2}}}\\ \Rightarrow {Z_{L1}} + \dfrac{{{Z_{L1}}}}{8} = {Z_{C1}} + 8{Z_{C1}}\\ \Rightarrow {Z_{L1}} = 8{Z_{C1}}\end{array}\)
Ta có: \(P = \dfrac{{{U^2}R}}{{{Z^2}}} = \dfrac{{{U^2}R}}{{Z_{C3}^2 - Z_{L3}^2}}\) và \({P_0} = \dfrac{{{U^2}R}}{{{R^2} + {{\left( {{Z_{{L_1}}} - {Z_{{C_1}}}} \right)}^2}}} = \dfrac{{{U^2}R}}{{Z_{L1}^2 - {Z_{L1}}{Z_C} + Z_{C1}^2}}\)
\( \Rightarrow \dfrac{{{P_0}}}{P} = \dfrac{{Z_{C3}^2 - Z_{L3}^2}}{{Z_{L1}^2 - {Z_{L1}}{Z_{C1}} + Z_{C1}^2}} = \dfrac{{16Z_{C1}^2 - 4Z_{C1}^2}}{{64Z_{C1}^2 - 8Z_{C1}^2 + Z_{C1}^2}} = \dfrac{{12}}{{57}} = \dfrac{4}{{19}}\)
Chọn B
Câu hỏi 42 :
Cho đoạn mạch AB như hình H1 với L là cuộn cảm thuần, R là biến trở. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có biểu thức \(u = U\sqrt 2 .\cos 2\pi ft\left( V \right)\), U không đổi nhưng f có thể thay đổi được. Hình H2 là đồ thị biểu diễn sự phụ thuộc của công suất tiêu thụ điện của mạch theo R là đường (1) khi f = f1 và là đường (2) khi f = f2. Bỏ qua điện trở của dây nối. Giá trị của Pmax gần nhất với giá trị nào sau đây?
- A 140 W
- B 260 W
- C 134 W
- D 280 W
Đáp án: C
Phương pháp giải:
Áp dụng công thức tính công suất :
\(P = {I^2}.R = \frac{{{U^2}.R}}{{{R^2} + {{({Z_L} - {Z_C})}^2}}}\)
Xác định điều kiện của R để Pmax
Từ đồ thị ta thấy:
\(\left\{ \begin{array}{l}
{P_{1\max }} = 100W \Leftrightarrow {R_1} = 120\Omega \\
{P_{21}} = 100W \Leftrightarrow {R_{21}} = 200\Omega
\end{array} \right.\)
Từ đó xác định U và R20 để tìm P2max
Lời giải chi tiết:
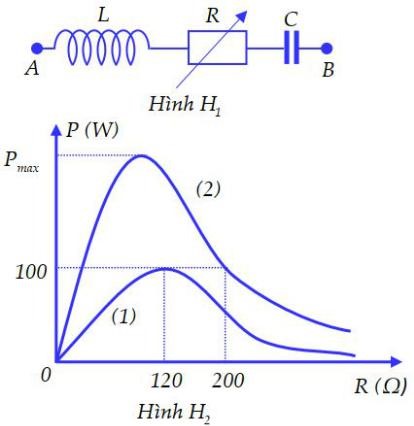
Công thức tính công suất :
\(P = {I^2}.R = \frac{{{U^2}.R}}{{{R^2} + {{({Z_L} - {Z_C})}^2}}} = \frac{{{U^2}}}{{R + \frac{{{{({Z_L} - {Z_C})}^2}}}{R}}}\)
Áp dụng công thức Cosi cho mẫu ta có :
\(R + \frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R} \ge 2.\left| {{Z_L} - {Z_C}} \right|\)
Do đó
\({P_{\max }} = \frac{{{U^2}}}{{2\left| {{Z_L} - {Z_C}} \right|}} \Leftrightarrow R = \left| {{Z_L} - {Z_C}} \right|\)
Từ đồ thị ta thấy :
\({P_{1\max }} = 100W \Leftrightarrow \frac{{{U^2}}}{{2{R_{10}}}} = 100 \Rightarrow {U^2} = 200.{R_{10}} = 200.120 = 24000\)
Và:
\(\begin{array}{l}
{P_2} = 100W \Leftrightarrow \frac{{{U^2}.{R_2}}}{{R_2^2 + {{\left( {{Z_{L2}} - {Z_{C2}}} \right)}^2}}} = 100 \Rightarrow \frac{{24000.200}}{{{{200}^2} + {{\left( {{Z_{L2}} - {Z_{C2}}} \right)}^2}}} = 100\\
\Rightarrow {\left( {{Z_{L2}} - {Z_{C2}}} \right)^2} = 8000 \Rightarrow \left| {{Z_{L2}} - {Z_{C2}}} \right| = \sqrt {8000}
\end{array}\)
Vậy :
\({P_{2\max }} = \frac{{{U^2}}}{{2.\left| {{Z_{L2}} - {Z_{C2}}} \right|}} = \frac{{24000}}{{2.\sqrt {8000} }} \approx 134W\)
Chọn C.
Câu hỏi 43 :
Mạch điện RCL nối tiếp có C thay đổi được. Điện áp hai đầu đoạn mạch \(u = 200\sqrt 2 \cos 100\pi t\,\,\left( V \right)\). Khi \(C = {C_1} = \dfrac{{50}}{\pi }\,\,\mu F\) thì mạch tiêu thụ công suất cực đại \({P_{\max }} = 160\,\,{\rm{W}}\). Khi \(C = {C_2} = \dfrac{1}{{5\pi }}\,\,mF\) thì điện áp hai đầu đoạn mạch RC và cuộn dây vuông pha với nhau, điện áp hiệu dụng hai đầu cuộn dây khi đó gần giá trị nào nhất sau đây
- A 90 V
- B 120 V
- C 75 V
- D 140 V
Đáp án: D
Phương pháp giải:
Dung kháng của tụ điện: \({Z_C} = \dfrac{1}{{\omega C}}\)
Mạch có cộng hưởng: \({P_{\max }} = \dfrac{{{U^2}}}{{R + r}};\,\,{Z_L} = {Z_C}\)
Điện áp hiệu dụng giữa hai đầu cuộn dây: \({U_d} = \dfrac{{U.\sqrt {{r^2} + {Z_L}^2} }}{{\sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Lời giải chi tiết:
Khi C = C1 và C = C2, dung kháng của tụ điện là:
\(\left\{ \begin{array}{l}{Z_{{C_1}}} = \dfrac{1}{{\omega {C_1}}} = \dfrac{1}{{100\pi .\dfrac{{{{50.10}^{ - 6}}}}{\pi }}} = 200\,\,\left( \Omega \right)\\{Z_{{C_2}}} = \dfrac{1}{{\omega {C_2}}} = \dfrac{1}{{100\pi .\dfrac{{{{1.10}^{ - 3}}}}{{5\pi }}}} = 50\,\,\left( \Omega \right)\end{array} \right.\)
Khi C = C1, trong mạch có cộng hưởng, khi đó:
\(\left\{ \begin{array}{l}{Z_L} = {Z_{{C_1}}} = 200\,\,\left( \Omega \right)\\{P_{\max }} = \dfrac{{{U^2}}}{{R + r}} \Rightarrow R + r = \dfrac{{{U^2}}}{{{P_{\max }}}} = \dfrac{{{{200}^2}}}{{160}} = 250\,\,\left( \Omega \right)\,\,\left( 1 \right)\end{array} \right.\)
Khi C = C2, uRC và urL vuông pha, ta có:
\(\begin{array}{l}\tan {\varphi _{{u_{RC}}}}.\tan {\varphi _{{u_{rL}}}} = - 1 \Rightarrow \dfrac{{ - {Z_{{C_2}}}}}{R}.\dfrac{{{Z_L}}}{r} = - 1\\ \Rightarrow R.r = {Z_{{C_2}}}.{Z_L} = 50.200 = 10000\,\,\left( 2 \right)\end{array}\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}R + r = 250\\R.r = 10000\end{array} \right. \Rightarrow \left\{ \begin{array}{l}R = 200\,\,\left( \Omega \right)\\r = 50\,\,\left( \Omega \right)\end{array} \right.\)
Điện áp hiệu dụng giữa hai đầu cuộn dây là:
\(\begin{array}{l}{U_d} = \dfrac{{U.\sqrt {{r^2} + {Z_L}^2} }}{{\sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_{{C_2}}}} \right)}^2}} }}\\ \Rightarrow {U_d} = \dfrac{{200.\sqrt {{{50}^2} + {{200}^2}} }}{{\sqrt {{{\left( {200 + 50} \right)}^2} + {{\left( {200 - 50} \right)}^2}} }} = 141\,\,\left( V \right)\end{array}\)
Chọn D.
Câu hỏi 44 :
Đặt điện áp xoay chiều có giá trị hiệu dụng U và tần số f không đổi vào hai đầu đoạn mạch AB nối tiếp theo thứ tự cuộn cảm thuần có độ tự cảm thay đổi, điện trở thuần và tụ điện. Gọi ULR là điện áp hiệu dụng đoạn mạch gồm cuộn cảm và điện trở, cosφ là hệ số công suất đoạn mạch AB. Đồ thị bên mô tả sự phụ thuộc của ULR và cosφ theo ZL. Giá trị của R gần nhất với giá trị nào sau đây?
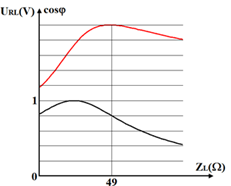
- A 25 Ω
- B 40 Ω
- C 50 Ω
- D 36 Ω
Đáp án: D
Phương pháp giải:
Hiệu điện thế \({U_{RL}} = \dfrac{{U.\sqrt {{R^2} + {Z_L}^2} }}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Hệ số công suất của mạch điện xoay chiều: \(\cos \varphi = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Lời giải chi tiết:
Từ đồ thị ta thấy khi ZL = 49 (Ω) thì ULRrmax, hệ số công suất của mạch bằng 0,8.
Khi ZL = 49 Ω, ta có:
\({U_{RL}} = \dfrac{U}{Z}.{Z_{LR}} = \dfrac{{U.\sqrt {{R^2} + {Z_L}^2} }}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \dfrac{U}{{\sqrt {1 + \dfrac{{{Z_C}^2 - 2.{Z_L}{Z_C}}}{{{R^2} + {Z_L}^2}}} }}\)
Đặt \(y = \dfrac{{{Z_C}^2 - 2{Z_L}{Z_C}}}{{{R^2} + {Z_L}^2}} \Rightarrow y' = \dfrac{{{Z_L}^2 - {R^2} - {Z_L}{Z_C}}}{{{{\left( {{R^2} + {Z_L}^2} \right)}^2}}}\)
Để \({U_{RL\max }} \Leftrightarrow {y_{\min }} \Leftrightarrow y' = 0 \Rightarrow {Z_L}^2 - {R^2} - {Z_L}{Z_C} = 0\)
\( \Rightarrow {Z_C} = {Z_L} - \dfrac{{{R^2}}}{{{Z_L}}} = 49 - \dfrac{{{R^2}}}{{49}}\)
Hệ số công suất của mạch khi đó là:
\(\begin{array}{l}\cos \varphi {\rm{ = }}\dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = 0,8\\ \Rightarrow \dfrac{R}{{\sqrt {{R^2} + {{\left[ {49 - \left( {49 - \dfrac{{{R^2}}}{{49}}} \right)} \right]}^2}} }} = 0,8\\ \Rightarrow \dfrac{R}{{\sqrt {{R^2} + {{\left( {\dfrac{{{R^2}}}{{49}}} \right)}^2}} }} = 0,8 \Rightarrow R = 36,75\,\,\left( \Omega \right)\end{array}\)
Chọn D.
Câu hỏi 45 :
Cho đoạn mạch AB gồm cuộn cảm thuần L, điện trở R = 50 Ω và tụ điện mắc nối tiếp theo thứ tự đó. Khi đặt vào hai đầu đoạn mạch AB điện áp \(u = 100\sqrt 2 \cos 100\pi t\,\,\left( V \right)\) (t tính bằng s) thì điện áp giữa hai đầu đoạn mạch chứa L và R có biểu thức \({u_{LR}} = 200\sqrt 2 \cos \left( {100\pi t + \dfrac{\pi }{3}} \right)\,\,\left( V \right)\). Công suất tiêu thụ của đoạn mạch AB bằng
- A 400 W.
- B 100 W.
- C 300 W.
- D 200 W.
Đáp án: D
Phương pháp giải:
Vẽ giản đồ vecto.
Sử dụng định lí hàm số cos và hàm số sin.
Công suất tiêu thụ của đoạn mạch: \(P = \dfrac{{{U^2}R}}{{{Z^2}}}\)
Lời giải chi tiết:
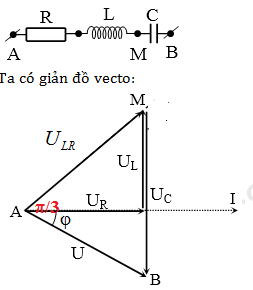
Áp dụng định lí hàm số cos ta có :
\(\begin{array}{l}U_C^2 = U_{LR}^2 + {U^2} - 2.{U_{LR}}.U.\cos \dfrac{\pi }{3}\\ \Rightarrow U_C^2 = {200^2} + {100^2} - 2.200.100.\dfrac{1}{2} = {3.10^4}\\ \Rightarrow {U_C} = 100\sqrt 3 V\end{array}\)
Áp dụng định lí hàm số sin ta có :
\(\begin{array}{l}\dfrac{{{U_{LR}}}}{{\sin \alpha }} = \dfrac{{{U_C}}}{{\sin \dfrac{\pi }{3}}} \Rightarrow \sin \alpha = \dfrac{{{U_{LR}}}}{{{U_C}}}.\sin \dfrac{\pi }{3} = \dfrac{{200}}{{100\sqrt 3 }}.\dfrac{{\sqrt 3 }}{2} = 1\\ \Rightarrow \alpha = {90^0} \Rightarrow \varphi = 0 \Rightarrow \overrightarrow U \uparrow \uparrow \overrightarrow {{U_R}} \end{array}\)
(Có cộng hưởng điện)
Công suất tiêu thụ của đoạn mạch AB : \(P = \dfrac{{{U^2}}}{R} = \dfrac{{{{100}^2}}}{{50}} = 200W\)
Chọn D.
Câu hỏi 46 :
Lần lượt mắc một điện trở R, một cuộn dây, một tụ điện C vào cùng một nguồn điện ổn định và đo cường độ dòng điện qua chúng thì được các giá trị (theo thứ tự) là 1A; 1A và 0A; điện năng tiêu thụ trên R trong thời gian ∆t khi đó là Q. Sau đó mắc nối tiếp các linh kiện trên cùng với một ampe kế nhiệt lí tưởng vào một nguồn ổn định thứ hai thì số chỉ ampe kế là 1A. Biết nếu xét trong cùng thời gian ∆t thì: điện năng tiêu thụ trên R khi chỉ mắc nó vào nguồn thứ hai là 4Q; còn khi mắc cuộn dây vào nguồn này thì điện năng tiêu thụ trong thời gian này cũng là Q. Hỏi nếu mắc điện trở R nối tiếp với tụ và ampe kế nhiệt vào nguồn thứ hai thì ampe kế chỉ bao nhiêu?
- A 2A
- B 1A
- C \(\sqrt 2 A\)
- D 0,5A
Đáp án: B
Phương pháp giải:
+ Điện năng tiêu thụ: \(Q = \dfrac{{{U^2}}}{R}.\Delta t\)
+ Công thức tính tổng trở và định luật Ôm: \(\left\{ \begin{array}{l}Z = \sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \\I = \dfrac{U}{Z}\end{array} \right.\)
+ Tụ điện cản trở hoàn toàn dòng điện không đổi.
Lời giải chi tiết:
+ Ban đầu cường độ dòng điện qua R. cuộn dây và C lần lượt là 1A; 1A; 0A, chứng tỏ dòng điện ban đầu là dòng điện không đổi, và cuộn dây có điện trở thuần bằng R.
Điên năng tiêu thụ ban đầu là: \(Q = \dfrac{{{U^2}}}{R}.\Delta t\)
+ Sau đó dùng dòng điện xoay chiều. Điện năng tiêu thụ khi đặt vào dòng điện lúc sau và chỉ có R là:
\(Q' = \dfrac{{U{'^2}}}{R}.\Delta t = 4Q \Leftrightarrow \dfrac{{U{'^2}}}{R} = 4\dfrac{{{U^2}}}{R} \Rightarrow U' = 2U\)
Khi cho dòng điện qua cuộn dây ta có:
\(Q'' = Q \Leftrightarrow \dfrac{{U{'^2}.R}}{{{R^2} + Z_L^2}}.\Delta t = \dfrac{{{U^2}}}{R}.\Delta t \Rightarrow {Z_L} = \sqrt 3 R\)
Khi mắc cả ba linh kiện vào dòng điện thừ 2 thì cường độ dòng điện là 1A. Ta có:
\(\begin{array}{l}\dfrac{{U'}}{{\sqrt {{{\left( {R + R} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{U}{R} \Leftrightarrow \dfrac{{2U}}{{\sqrt {{{\left( {2R} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{U}{R}\\ \Rightarrow {Z_L} = {Z_C} = \sqrt 3 R\end{array}\)
Khi mắc điện trở với tụ vào mạch thứ hai thì cường độ dòng điện là:
\(I = \dfrac{{U'}}{{\sqrt {{R^2} + Z_C^2} }} = \dfrac{{2U}}{{\sqrt {{R^2} + 3{R^2}} }} = \dfrac{U}{R} = 1A\)
Chọn B.
Câu hỏi 47 :
Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu đoạn mạch gồm biến trở, cuộn dây và tụ điện mắc nối tiếp. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của công suất tỏa nhiệt P trên biến trở và hệ số công suất \(cos\varphi \) của đoạn mạch theo giá trị R của biến trở. Điện trở của cuộn dây có giá trị gần nhất với giá trị nào sau đây?
- A
\(10,1\Omega \)
- B \(9,1\Omega \)
- C \(7,9\Omega \)
- D \(11,2\Omega \)
Đáp án: C
Phương pháp giải:
+ Đọc đồ thị
+ Sử dụng biểu thức tính công suất: \(P = {I^2}R\)
+ Bài toán cuộn dây không thuần cảm, công suất trên biến trở cực đại
+ Sử dụng biểu thức tính hệ số công suất: \(cos\varphi = \dfrac{R}{Z}\)
Lời giải chi tiết:
Từ đồ thị, ta có khi \(R = 30\Omega \) thì hệ số công suất của mạch bằng \(0,8\) và công suất tiêu thụ của biến trở đạt cực đại.
Mặt khác, công suất trên biến trở:
\({P_R} = {I^2}R = \dfrac{{{U^2}}}{{{Z^2}}}.R = \dfrac{{{U^2}}}{{{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}R\)
Công suất trên biến trở cực đại \(\left( {{P_{{R_{max}}}}} \right)\) khi \({R^2} = {r^2} + {\left( {{Z_L} - {Z_C}} \right)^2}\)
\( \Leftrightarrow {30^2} = {r^2} + {\left( {{Z_L} - {Z_C}} \right)^2}\) (1)
Hệ số công suất của mạch khi đó: \(cos\varphi = \dfrac{{R + r}}{Z} \Leftrightarrow 0,8 = \dfrac{{R + r}}{{\sqrt {{{\left( {R + r} \right)}^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
\( \Rightarrow \left| {{Z_L} - {Z_C}} \right| = 0,75\left( {R + r} \right)\) (2)
Từ (1) và (2) ta suy ra: \({30^2} = {r^2} + 0,{75^2}{\left( {30 + r} \right)^2}\)
\( \Rightarrow r = 8,4\Omega \) gần đáp án C nhất
Chọn C
Câu hỏi 48 :
Cho đoạn mạch \(AB\) gồm hai đoạn mạch \(AM\) và \(MB\) mắc nối tiếp. Đoạn mạch \(AM\) gồm cuộn dây thuần cảm nối tiếp với tụ điện theo thứ tự đó, đoạn mạch \(MB\) chỉ có điện trở thuần \(R\). Điện áp đặt vào \(AB\) có biểu thức \(u = 80\sqrt 2 \cos \left( {100\pi t} \right)\,V\), hệ số công suất của đoạn mạch \(AB\) là \(\dfrac{{\sqrt 2 }}{2}.\) Khi điện áp tức thời giữa hai điểm \(A\) và \(M\) là 48 V thì điện áp tức thời giữa hai điểm \(M\) và \(B\) có độ lớn là
- A 64 V.
- B 102,5 V.
- C 48 V.
- D 56 V.
Đáp án: A
Phương pháp giải:
Sử dụng giản đồ vecto.
Hệ số công suất của đoạn mạch: \(\cos \varphi = \dfrac{R}{Z}\)
Lời giải chi tiết:
+ Ta có giản đồ vecto:
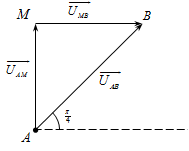
Hệ số công suất của đoạn mạch:
\(\cos \varphi = \dfrac{{\sqrt 2 }}{2} \Rightarrow \varphi = \dfrac{\pi }{4} \Rightarrow \) \(\Delta AMB\) vuông cân tại \(M\)
\( \Rightarrow {U_{0AM}} = {U_{0MB}} = \dfrac{{{U_0}}}{{\sqrt 2 }} = \dfrac{{80\sqrt 2 }}{{\sqrt 2 }} = 80V\)
+ Lại có \({u_{AM}}\)vuông pha với \({u_{MB}}\)
\(\begin{array}{l} \Rightarrow {\left( {\dfrac{{{u_{AM}}}}{{{U_{0AM}}}}} \right)^2} + {\left( {\dfrac{{{u_{MB}}}}{{{U_{0MB}}}}} \right)^2} = 1\\ \Rightarrow u_{MB}^2 = \sqrt {U_{0AM}^2 - u_{AM}^2} = \sqrt {{{80}^2} - {{48}^2}} = 64V\end{array}\)
Chọn A.
Câu hỏi 49 :
Đặt điện áp xoay chiều \(u = {U_0}\cos 100\pi t\left( V \right)\) (U0 không đổi, t tính bằng s) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở R = 40 Ω và cuộn dây có điện trở thì điện áp hiệu dụng giữa hai đầu cuộn dây là Ud. Lần lượt thay R bằng cuộn cảm thuần có độ tự cảm \(\dfrac{{0,2}}{\pi }H\), rồi thay L bằng tụ điện C có điện dung \(\dfrac{{{{10}^{ - 4}}}}{\pi }F\) thì điện áp hiệu dụng giữa hai đầu cuộn dây trong hai trường hợp đều bằng Ud. Hệ số công suất của cuộn dây bằng
- A 0,747.
- B 0,124.
- C 0,707.
- D 0,447.
Đáp án: B
Phương pháp giải:
Cảm kháng của cuộn dây thuần cảm: \({Z_L} = \omega L\)
Dung kháng của tụ điện: \({Z_C} = \dfrac{1}{{\omega C}}\)
Hệ số công suất: \(\cos \varphi = \dfrac{R}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\)
Lời giải chi tiết:
Cảm kháng của cuộn dây thuần cảm và dung kháng của tụ điện là:
\(\left\{ \begin{array}{l}{Z_L} = \omega L = 100\pi .\dfrac{{0,2}}{\pi } = 20\,\,\left( \Omega \right)\\{Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\,\,\left( \Omega \right)\end{array} \right.\)
Điện áp hiệu dụng trong cả 3 trường hợp đều bằng Ud → tổng trở trong cả 3 trường hợp là như nhau:
\({\left( {R + r} \right)^2} + {Z_{{L_0}}}^2 = {\left( {{Z_L} + {Z_{{L_0}}}} \right)^2} + {r^2} \Rightarrow {\left( {40 + r} \right)^2} + {Z_{{L_0}}}^2 = {r^2} + {\left( {20 + {Z_{{L_0}}}} \right)^2}\,\,\left( 1 \right)\)
\({r^2} + {\left( {{Z_L} + {Z_{{L_0}}}} \right)^2} = {r^2} + {\left( {{Z_{{L_0}}} - {Z_C}} \right)^2} \Rightarrow {r^2} + {\left( {20 + {Z_{{L_0}}}} \right)^2} = {r^2} + {\left( {{Z_{{L_0}}} - 100} \right)^2}\,\,\left( 2 \right)\)
Từ (1) và (2), ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}{\left( {40 + r} \right)^2} + {Z_{{L_0}}}^2 = {r^2} + {\left( {20 + {Z_{{L_0}}}} \right)^2}\\{r^2} + {\left( {20 + {Z_{{L_0}}}} \right)^2} = {r^2} + {\left( {{Z_{{L_0}}} - 100} \right)^2}\end{array} \right.\\ \Rightarrow 20 + {Z_{{L_0}}} = 100 - {Z_{{L_0}}} \Rightarrow {Z_{{L_0}}} = 40\,\,\left( \Omega \right)\\ \Rightarrow {\left( {40 + r} \right)^2} + {40^2} = {r^2} + {\left( {20 + 40} \right)^2} \Rightarrow r = 5\,\,\left( \Omega \right)\end{array}\)
Hệ số công suất của cuộn dây là:
\(\cos {\varphi _d} = \dfrac{r}{{{Z_d}}} = \dfrac{r}{{\sqrt {{r^2} + {Z_{{L_0}}}^2} }} = \dfrac{5}{{\sqrt {{5^2} + {{40}^2}} }} = 0,124\)
Chọn B.
Câu hỏi 50 :
Cho đoạn mạch mắc nối tiếp gồm biến trở R, cuộn cảm thuần L và tụ điện C. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có giá trị hiệu dụng U và tần số f không đổi. Khi giá trị biến trở là R1 và R2 thì công suất tiêu thụ của đoạn mạch tương ứng là P1 và P2 độ lệch pha giữa điện áp và cường độ dòng điện trong đoạn mạch tương ứng là φ1 và φ2. Cho R1 = 2R2; \({\cos ^2}{\varphi _1} + {\cos ^2}{\varphi _2} = \frac{7}{{10}}\). Tỉ số \(\frac{{{P_1}}}{{{P_2}}}\) bằng
- A \(\frac{5}{4}\)
- B \(\frac{3}{5}\)
- C \(\frac{4}{5}\)
- D \(\frac{5}{3}\)
Đáp án: A
Phương pháp giải:
Công thức tính công suất
\(P = U.I.\cos \varphi \)
Lời giải chi tiết:
Công suất khi R = R1 là:
\({P_1} = U.{I_1}.\cos {\varphi _1} = \frac{{{U^2}}}{{\sqrt {{R_1}^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}.\cos {\varphi _1}\)
Công suất khi R = R2 là:
\({P_2} = U.{I_2}.\cos {\varphi _2} = \frac{{{U^2}}}{{\sqrt {{R_2}^2 + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}.\cos {\varphi _2}\)
Từ đề bài ta có:
\(\begin{array}{l}
{\cos ^2}{\varphi _1} + {\cos ^2}{\varphi _2} = \frac{7}{{10}}\\
\Rightarrow \frac{1}{{1 + {{\tan }^2}{\varphi _1}}} + \frac{1}{{1 + {{\tan }^2}{\varphi _2}}} = \frac{7}{{10}} \Leftrightarrow \frac{1}{{1 + {{\left( {\frac{{{Z_{LC}}}}{{{R_1}}}} \right)}^2}}} + \frac{1}{{1 + {{\left( {\frac{{{Z_{LC}}}}{{{R_2}}}} \right)}^2}}} = \frac{7}{{10}}\\
\Leftrightarrow \frac{1}{{1 + {{\left( {\frac{{{Z_{LC}}}}{{{R_1}}}} \right)}^2}}} + \frac{1}{{1 + {{\left( {\frac{{{Z_{LC}}}}{{\frac{1}{2}{R_1}}}} \right)}^2}}} = \frac{7}{{10}} \Leftrightarrow \frac{1}{{1 + {{\left( {\frac{{{Z_{LC}}}}{{{R_1}}}} \right)}^2}}} + \frac{1}{{1 + 4{{\left( {\frac{{{Z_{LC}}}}{{{R_1}}}} \right)}^2}}} = \frac{7}{{10}}
\end{array}\)
Đặt \({\left( {\frac{{{Z_{LC}}}}{{{R_1}}}} \right)^2} = x;\,\,\left( {x > 0} \right)\) ta được:
\(\begin{array}{l}
\frac{1}{{1 + x}} + \frac{1}{{1 + 4x}} = \frac{7}{{10}} \Rightarrow \frac{{5x + 2}}{{4{x^2} + 5x + 1}} = \frac{7}{{10}}\\
\Rightarrow 10.(5x + 2) = 7.(4{x^2} + 5x + 1)\\
\Leftrightarrow 28{x^2} - 15x - 13 = 0 \Rightarrow \left[ \begin{array}{l}
{x_1} = 1\,\,\,(tm)\\
{x_2} = - \frac{{13}}{{28}}\,\,(loai)
\end{array} \right.
\end{array}\)
Vậy:
\(\begin{array}{l}
\frac{{{Z_{LC}}}}{{{R_1}}} = 1 \Leftrightarrow {Z_{LC}} = {R_1} \Rightarrow \tan {\varphi _1} = 1 \Rightarrow {\varphi _1} = {45^0} \Rightarrow \cos {\varphi _1} = \frac{1}{{\sqrt 2 }}\\
\tan {\varphi _2} = 2\tan {\varphi _1} = 2 \Rightarrow \cos {\varphi _2} = \sqrt {\frac{1}{{1 + \tan {\varphi _2}}}} = \frac{1}{{\sqrt 5 }}
\end{array}\)
Tỉ số :
\(\begin{array}{l}
\frac{{{P_1}}}{{{P_2}}} = \frac{{{U^2}.\cos {\varphi _1}}}{{\sqrt {{R_1}^2 + Z_{LC}^2} }}.\frac{{\sqrt {R_2^2 + Z_{LC}^2} }}{{{U^2}.\cos {\varphi _2}}} = \frac{1}{{\sqrt 2 }}.\frac{1}{{\sqrt {{R_1}^2 + R_1^2} }}.\frac{{\sqrt {\frac{1}{4}R_1^2 + R_1^2} }}{{\frac{1}{{\sqrt 5 }}}} = \frac{5}{4}\\
\end{array}\)
Chọn A.