Đại Số 11: Nhị thức Niu – Tơn Bài 1 2 3 4 5 6 trang 57,58 SGK

Đáp án và hướng dẫn Giải bài 1 trang 57; bài 2,3,4,5,6 trang 58 sgk đại số và giải tích 11: Nhị thức Niu – Tơn – chương 2.

Bài 1. Viết khai triển theo công thức nhị thức Niu – Tơn:
a) (a + 2b)⁵;                          b) (a – √2)⁶;

c) (x – 1/x)¹³.

Đáp án: a) Theo dòng 5 của tam giác Pascal, ta có:

(a + 2b)⁵= a⁵ + 5a⁴ (2b) + 10a³(2b)² + 10a² (2b)³ + 5a (2b)⁴ + (2b)⁵

= a⁵ + 10a⁴b + 40a³b² + 80a²b³ + 80ab⁴ + 32b⁵

b) Theo dòng 6 của tam giác Pascal, ta có:

(a – √2)⁶ = [a + (-√2)]⁶ = a⁶ + 6a⁵ (-√2) + 15a⁴ (-√2)² + 20a³ (-√2)³ + 15a² (-√2)⁴ + 6a(-√2)⁵ + (-√2)⁶.

= a⁶ – 6√2a⁵ + 30a⁴ – 40√2a³ + 60a² – 24√2a + 8.

c) Theo công thức nhị thức Niu – Tơn, ta có:

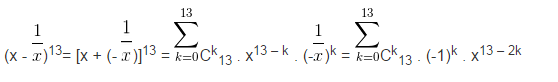
Nhận xét: Trong trường hợp số mũ n khá nhỏ (chẳng hạn trong các câu a) và b) trên đây) thì ta có thể sử dụng tam giác Pascal để tính nhanh các hệ số của khai triển.

Bài 2 trang 58. Tìm hệ số của x³ trong khai triển của biểu thức: https://dapandethi.vn/storage/solutions/bai2-nhi-thuc-new-ton.png" />

Giải:

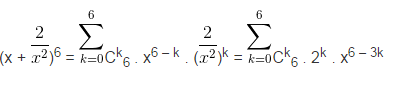
Trong tổng này, số hạng C^k₆ . 2^k . x^{6 – 3k} có số mũ của x bằng 3 khi và chỉ khi

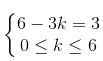
Do đó hệ số của x³ trong khai triển của biểu thức đã cho là:

2 . C¹₆ = 2 . 6 = 12.

Bài 3. Biết hệ số của x²trong khai triển của (1 – 3x)ⁿ là 90. Tìm n.

Giải: Với số thực x ≠ 0 và với mọi số tự nhiên n ≥ 1, ta có:

(1 – 3x)ⁿ = [1 – (3x)]ⁿ = https://dapandethi.vn/storage/solutions/dai-so-11-nhi-thuc-new-ton.pngC^k_n (1)^{n – k} (-3)^k . x^k.

Suy ra hệ số của x²trong khai triển này là 3²C²_n .Theo giả thiết, ta có:

3²C²_n = 90 => C²_n = 10.

Từ đó ta có:

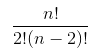
= 10 ⇔ n(n – 1) = 20.

⇔ n² – n – 20 = 0 ⇔ n = -4 (loại) hoặc n = 5.

ĐS: n = 5.

Bài 4 Đại số và giải tích lớp 11. Tìm số hạng không chứa x trong khai triển của (x³+1/x)⁸

Giải: Ta có: (x³ +1/x)⁸=https://dapandethi.vn/storage/solutions/nhi-thuc-new-ton2.png" />

Trong tổng này, số hạng C^k₈ x^{24 – 4k} không chứa x khi và chỉ khi

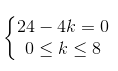
⇔ k = 6.

Vậy số hạng không chứa x trong khai triển (theo công thức nhị thức Niu – Tơn) của biểu thức đã cho là C⁶₈ = 28.

Bài 5. Từ khai triển biểu thức (3x – 4)¹⁷ thành đa thức, hãy tính tổng các hệ số của đa thức nhận được:

Tổng các hệ số của đa thức f(x) = (3x – 4)¹⁷ bằng:

f(1) = (3 – 4)¹⁷= (– 1)¹⁷ = -1.

Bài 6 trang 58 . Chứng minh rằng:
a) 11¹⁰ – 1 chia hết cho 100;

b) 101¹⁰⁰– 1 chia hết cho 10 000;

c) √10[(1 + √10)¹⁰⁰ – (1- √10)¹⁰⁰] là một số nguyên.

Giải:

a) 11¹⁰ – 1 = (1 + 10)¹⁰ – 1 = (1 + C¹₁₀ 10 + C²₁₀10² + … +C⁹₁₀ 10⁹ + 10¹⁰) – 1

= 10² + C²₁₀10² +…+ C⁹₁₀ 10⁹ + 10¹⁰.

Tổng sau cùng chia hết cho 100 suy ra 11¹⁰ – 1 chia hết cho 100.

b) Ta có

101¹⁰⁰ – 1 = (1 + 100)¹⁰⁰ – 1

= (1 + C¹₁₀₀ 100 + C²₁₀₀ 100² + …+C⁹⁹₁₀₀ 100⁹⁹ + 100¹⁰⁰) – 1.

= 100² + C²₁₀₀100² + …+C⁹⁹₁₀₀100⁹⁹ + 100¹⁰⁰.

Tổng sau cùng chia hết cho 10 000 suy ra 101¹⁰⁰ – 1 chia hết cho 10 000.

c)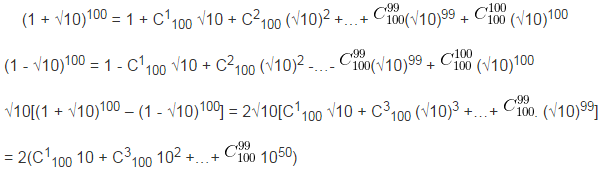

Tổng sau cùng là một số nguyên, suy ra √10[(1 + √10)¹⁰⁰ – (1 – √10)¹⁰⁰] là một số nguyên.

Các em cũng có thể ôn lại kiến thức phần Nhị Thức Niu Tơn bằng video dưới đây.

https://youtu.be/hOofxE84TAA